Let’s get to the point, the parts of a division are the following:
- Divisor: It is the number of parts into which a number is going to be divided
- Quotient: It is the result of division. More specifically, it is the size of each part of the number that was divided by the divisor.
- Dividend: It is the number to divide.
- Remainder: It is the remainder that is left by making a division by hand before reaching the decimals. When a division has zero remainder it is because it can no longer be divided, these are called exact divisions. But when it does not have a zero remainder, it is because divisions can continue, these are called integer divisions.
The following image looks more illustrative
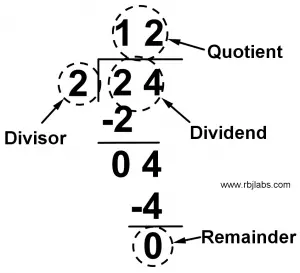
Graphic example of division
Let’s see the graphical representation of a division, because seeing many numbers is a bit annoying. It is necessary so that we have another representation of the divisions, let’s see figure 2:

Point B is exactly in the middle between point A and C. Taking as reference figure 1 which is the number 24 divided by 2, we can see that the total that in this case is the number 24 and we will divide it by 2.
What we can see is that the segment \overline{AB} and the segment \overline{BC} measure the same, since what we did is divide the 24 by 2 as the division of the Figure 1 says.
The segment \overline{AB} and the segment \overline{BC} measure 12, which is exactly the result of the division in Figure 1.
24 / 2 = 12 \ \longrightarrow \ \overline{AB} = \overline{BC} = 12
To emphasize, the result of a division is the length or size of a number or object, even if the division has decimals, it is always the same principle. As simple as that.
Thank you for being in this moment with us : )
