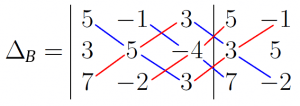
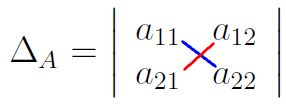The first thing to be clear is that we always have to work with a determinant of n \times n, what we mean is that it has to be a square matrix. Note: later we will see the determinants of systems of linear equations.
The determinant symbol for matrices of order n is represented as \Delta_{n}, a determinant of n \ rows and n\ columns, now we see it below, quiet. There are authors who use a letter to represent the columns and a number as a subscript to represent the rows:
\Delta_{n} = \left| \begin{array}{c c c c} a_{1} & b_{1} & \dots & z_{1} \\ a_{2} & b_{2} & \dots & z_{2} \\ \dots & \dots & \dots & \dots \\ a_{n} & b_{n} & \dots & z_{n} \end{array} \right|And there are authors that use the same letter as a base and its subscripts mean the rows and columns respectively, that means that a_{2 1} refers to the value that is in row 2, column 1, let’s see the example:
\Delta_{n} = \left| \begin{array}{c c c c} a_{1 1} & a_{1 2} & \dots & a_{1 n} \\ a_{2 1} & a_{2 2} & \dots & a_{2 n} \\ \dots & \dots & \dots & \dots \\ a_{n 1} & a_{n 2} & \dots & a_{n n} \end{array} \right|With that we are ready to move on to the examples, the notation that we will use is that of the second example.
Determinants of second order
When we talk about determinants of second order, we talk that we will calculate determinants of square matrices of 2 \times 2. Let’s calculate the determinant of the matrix l:
l = \left[ \begin{array}{c c} 3 & 5 \\ 2 & 6 \\ \end{array} \right]To calculate the determinants of the matrices of 2 \times 2, you have to multiply the numbers of the blue diagonal minus the multiplication of the numbers of the red diagonal:
\Delta_{A} = a_{11}\cdot a_{22} - [a_{21} \cdot a_{12}]
Ok, now let’s proceed to calculate the determinant of the l matrix:
\Delta_{l} = \left| \begin{array}{c c} 3 & 5 \\ 2 & 6 \\ \end{array} \right| = 3\cdot 6 - [2\cdot 5] = 8So we observe that the determinant of the matrix l equals 8.
That’s all you need to calculate determinants of 2 \times 2 matrices.
Determinants of third order
For the calculation of third order determinants we will use something peculiar that is only to make it more comfortable to look at, which is to add two more columns, but when you take some practice, the determinant will be done without doing this of add the two more columns Well, let’s see our next matrix:
B = \left[ \begin{array}{c c c} 5 & -1 & 3 \\ 3 & 5 & -4 \\ 7 & -2 & 3 \end{array} \right]To calculate the determinant of the B matrix, we are going to add the first two columns one more time:
\Delta_{B} =\left| \begin{array}{c c c | c c} 5 & -1 & 3 & 5 & -1 \\ 3 & 5 & -4 & 3 & 5 \\ 7 & -2 & 3 & 7 & -2 \end{array}\right.Now, to calculate the determinant of the matrix B, we will sum the multiplication of each blue diagonal and then we will subtract the sum of each multiplication of each red diagonal, visually it looks like this:
\Delta_{B} = 5\cdot 5 \cdot 3 + (-1)\cdot (-4) \cdot 7 + 3\cdot 3 \cdot(-2) -
\left[ 7 \cdot 5 \cdot 3 + (-2) \cdot (-4) \cdot 5 + 3\cdot 3 \cdot (-1) \right]
Finally we just have to solve all the operations and we will have the determinant, let’s go step by step, let’s solve all the multiplications:
\Delta _{B} = 75 + 28 - 18 - [105 + 40 - 9]
Now let’s eliminate the brackets:
\Delta_{B} = 75 + 28 - 18 - 105 - 40 + 9
Finally proceed to perform the addition and subtraction:
\Delta_{B} = -51
So the determinant of our matrix of 3\times 3 is -51!
Great, you already know how to calculate determinants of 2×2 matrices and 3×3 matrices!
Determinants of systems of linear equations
We have come to something more peculiar, quite simple and useful. The calculation of determinants of systems of linear equations of n\times n serves to find the values of the unknowns, as we can find the values of the unknowns of the systems of linear equations of 2\times 2:
\begin{array}{l} x + 2y = 1 \\ x + y = 1 \end{array}Where:
x = 1 \quad y = 0
Or in a system of equations 3\times 3:
\begin{array}{l} x + y + z = 1 \\x + 2y + z = 1 \\x + y + 3z = 1 \end{array}Where:
x = 1 \quad y = 0 \quad z = 0
The number of unknowns will tell what size is the system of linear equations, if you have two unknowns, the system of equations is 2\times 2, if you have three unknowns, the system of equations is 3\times 3 and so successively.
To find the values of the unknowns, we must apply the Cramer rule with which the determinants of the matrices of the unknowns are divided among the determinant of the system matrix. Let’s quickly see the following example:
\begin{array}{l} a_{11}x + a_{12}y + a_{13}z = r_{1} \\ a_{21}x + a_{22}y + a_{23}z = r_{2} \\ a_{31}x + a_{32}y + a_{33}z = r_{3} \end{array}Our matrix is the following:
s =\left( \begin{array}{c c c | c} a_{11} & a_{12} & a_{13} & r_{1} \\ a_{21} & a_{22} & a_{23} & r_{2} \\ a_{31} & a_{32} & a_{33} & r_{3} \end{array}\right)To find the values of the unknowns, we will find the determinant of the system matrix (remember that the values of r_{1}, r_{2} and r_{3} are ignored to calculate the matrix system for the determinant of s):
\Delta_{s} = \left| \begin{array}{c c c} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right |We will do exactly the same as we did the sum of the product of the blue diagonals minus the sum of the product of the red diagonals, the same as we did above the post:
\Delta_{s} = \begin{array}{|c c c | c c} a_{11} & a_{12} & a_{13} & a_{11} & a_{12} \\ a_{21} & a_{22} & a_{23} & a_{21} & a_{22} \\ a_{31} & a_{32} & a_{33} & a_{31} & a_{32} \end{array}\Delta_{s} = a_{11}\cdot a_{22} \cdot a_{33} + a_{12} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot a_{32} -
\left[ a_{31}\cdot a_{22} \cdot a_{13} + a_{32} \cdot a_{23} \cdot a_{11} + a_{33} \cdot a_{21} \cdot a_{12}\right]
We will find the determinant of x, where the matrix for the determinant of x is the same system matrix only in the first column we will write the values of r_{1}, r_{2} and r_{3} respectively:
x = \left[ \begin{array}{c c c} r_{1} & a_{12} & a_{13} \\ r_{2} & a_{22} & a_{23} \\ r_{3} & a_{32} & a_{33} \end{array}\right ]We will do exactly the same as we did of the sum of the product of the blue diagonals minus the sum of the product of the red diagonals:
\Delta_{x} = \begin{array}{|c c c | c c} r_{1} & a_{12} & a_{13} & r_{1} & a_{12} \\ r_{2} & a_{22} & a_{23} & r_{2} & a_{22} \\ r_{3} & a_{32} & a_{33} & r_{3} & a_{32} \end{array}\Delta_{x} = r_{1}\cdot a_{22} \cdot a_{33} + a_{12} \cdot a_{23} \cdot r_{3} + a_{13} \cdot r_{2} \cdot a_{32} -
\left[ r_{3}\cdot a_{22} \cdot a_{13} + a_{32} \cdot a_{23} \cdot r_{1} + a_{33} \cdot r_{2} \cdot a_{12}\right]
To find the determinant for the y matrix, we do the same procedure as we did for the x matrix, we take the system matrix but now we will change the second column for the values of r_{1}, r_{2} and r_{3} respectively:
y = \left[ \begin{array}{c c c} a_{11} & r_{1} & a_{13} \\ a_{21} & r_{2} & a_{23} \\ a_{31} & r_{3} & a_{33} \end{array}\right ]\Delta_{y} = \begin{array}{|c c c | c c} a_{11} & r_{1} & a_{13} & a_{11} & r_{1} \\ a_{21} & r_{2} & a_{23} & a_{21} & r_{2} \\ a_{31} & r_{3} & a_{33} & a_{31} & r_{3} \end{array}\Delta_{y} = a_{11}\cdot r_{2} \cdot a_{33} + r_{1} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot r_{3} -
\left[ a_{31}\cdot r_{2} \cdot a_{13} + r_{3} \cdot a_{23} \cdot a_{11} + a_{33} \cdot a_{21} \cdot r_{1}\right]
To find the determinant for the z matrix, we do the same procedure as we did for the x matrix, we take the matrix of the system but now we will change the third column for the values of r_{1}, r_{2} and r_{3} respectively:
z = \left[ \begin{array}{c c c} a_{11} & a_{12} & r_{1} \\ a_{21} & a_{22} & r_{2} \\ a_{31} & a_{32} & r_{3} \end{array}\right ]\Delta_{z} = \begin{array}{|c c c | c c} a_{11} & a_{12} & r_{1} & a_{11} & a_{12} \\ a_{21} & a_{22} & r_{2} & a_{21} & a_{22} \\ a_{31} & a_{32} & r_{3} & a_{31} & a_{32} \end{array}\Delta_{z} = a_{11}\cdot a_{22} \cdot r_{3} + a_{12} \cdot r_{2} \cdot a_{31} + r_{1} \cdot a_{21} \cdot a_{32} -
\left[ a_{31}\cdot a_{22} \cdot r_{1} + a_{32} \cdot r_{2} \cdot a_{11} + r_{3} \cdot a_{21} \cdot a_{12}\right]
Once we find the determinants of each matrix, we will apply Cramer’s rule to obtain the final values:
x = \cfrac{\Delta_{x}}{\Delta_{s}}
y = \cfrac{\Delta_{y}}{\Delta_{s}}
z = \cfrac{\Delta_{z}}{\Delta_{s}}
Example of determinants
In the following example we will use a system of 3\times 3 equations with which we will use the determinant method to find the values of x, y and z. Let’s solve the following system of linear equations:
\begin{array}{l} 4x - 2y + 2z = 36 \\ 2x + 4y - 5z = 28 \\ 6x - 3y + 2z = 24 \end{array}Where our matrix will look like this:
s = \left(\begin{array}{c c c | c} a_{11} & a_{12} & a_{13} & r_{1} \\ a_{21} & a_{22} & a_{23} & r_{2} \\ a_{31} & a_{32} & a_{33} & r_{3} \end{array}\right) = \left(\begin{array}{c c c | c} 4 & -2 & 2 & 36 \\ 2 & 4 & -5 & 28 \\ 6 & -3 & 2 & 24 \end{array}\right)To solve the system of linear equations shown, we have to find the determinant of the system (s), the determinant of x, the determinant of y and the determinant of z, so first let’s find the determinant of the system as we have seen above of the post, add the two columns and carry out the corresponding operations:
\Delta_{s} = \left | \begin{array}{c c c | c c} 4 & -2 & 2 & 4 & -2\\ 2 & 4 & -5 & 2 & 4\\ 6 & -3 & 2 & 6 & -3 \end{array}\right .\Delta_{s}=4 \cdot 4 \cdot 2 + (-2)\cdot(-5)\cdot 6 + 2 \cdot 2 \cdot(-3) -
\left[ 6\cdot4\cdot2 + (-3)\cdot(-5)\cdot 4 + 2\cdot2 \cdot(-2) \right]
\Delta_{s} = -20
Now let’s find the \Delta_{x}, change the first column by the values of r_{1}, r_{2} and r_{3}
\Delta_{x} = \left | \begin{array}{c c c} 36 & -2 & 2 \\ 28 & 4 & -5 \\ 24 & -3 & 2 \end{array}\right |Let’s add the two more columns so that when making the multiplication it becomes easier visually:
\Delta_{x} = \left | \begin{array}{c c c | c c} 36 & -2 & 2 & 36 & -2 \\ 28 & 4 & -5 & 28 & 4 \\ 24 & -3 & 2 & 24 & -3 \end{array}\right.Now proceed to write the corresponding operations:
\Delta_{x} = 36 \cdot 4 \cdot 2 + (-2)\cdot(-5)\cdot 24 + 2 \cdot 28 \cdot(-3) -
\left[ 24 \cdot 4 \cdot 2 + (-3)\cdot(-5)\cdot 36 + 2 \cdot 28 \cdot(-2) \right]
Doing all the operations we will have the following result:
\Delta_{x} = -260
Let’s find the \Delta_{y}, change the values of the second column by the values of r_{1}, r_{2} and r_{3}:
\Delta_{y} = \left | \begin{array}{c c c} 4 & 36 & 2 \\ 2 & 28 & -5 \\ 6 & 24 & 2 \end{array}\right |Proceed to add the two more columns only to make it easier visually when performing operations:
\Delta_{y} = \left|\begin{array}{c c c | c c} 4 & 36 & 2 & 4 & 36 \\ 2 & 28 & -5 & 2 & 28\\ 6 & 24 & 2 & 6 & 24 \end{array} \right.\Delta_{y} = 4 \cdot 28 \cdot 2 + 36\cdot(-5)\cdot 6 + 2 \cdot 2 \cdot 24 -
\left[ 6 \cdot 28 \cdot 2 + 24 \cdot (-5) \cdot 4 + 2 \cdot 2 \cdot 36 \right]
\Delta_{y} = -760
Finally find the \Delta_{z}, change the values of the third column by the values of r_{1}, r_{2} and r_{3} respectively:
\Delta_{z} = \left | \begin{array}{c c c} 4 & -2 & 36 \\ 2 & 4 & 28 \\ 6 & -3 & 24 \end{array}\right |Now let’s add the two more columns to make operations easier visually:
\Delta_{z} = \left | \begin{array}{c c c | c c} 4 & -2 & 36 & 4 & -2 \\ 2 & 4 & 28 & 2 & 4 \\ 6 & -3 & 24 & 6 & -3 \end{array}\right .\Delta_{z} = 4 \cdot 4 \cdot 24 + (-2) \cdot 28 \cdot 6 + 36 \cdot 2 \cdot(-3) -
\left[ 6 \cdot 4 \cdot 36 + (-3) \cdot 28 \cdot 4 + 24 \cdot 2 \cdot(-2) \right]
\Delta_{z} = -600
With all the determinants found, we can proceed to carry out the divisions that will tell us each value of the unknowns:
x = \cfrac{\Delta_{x}}{\Delta_{s}} = \cfrac{-260}{-20} = 13
y = \cfrac{\Delta_{y}}{\Delta_{s}} = \cfrac{-760}{-20} = 38
z = \cfrac{\Delta_{z}}{\Delta_{s}} = \cfrac{-600}{-20} = 30
Yes now! Our final results of our unknowns are:
x = 13 \qquad y = 38 \qquad z = 30
Thank you for being at this moment with us : )