To start with this post, we will first show the summary of the real numbers with a simple image and then we will explain each component of the image.
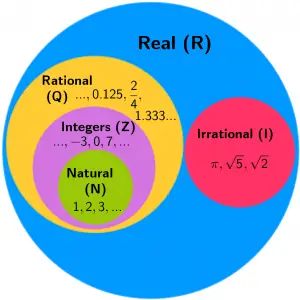
Real Numbers (R)
All rational and irrational numbers correspond to a real number. Of which, rational numbers are made up of whole numbers, natural numbers, negative numbers, and zero.
Real numbers are all those that can be represented within a number line, regardless of whether the number is negative, positive, rational or irrational decimal, integer or zero.

Properties of real numbers
\begin{array}{c c} \hline \hline \begin{array}{c} \text{Commutative} \\ \text{Property} \end{array} & \begin{array}{c} a + b = b + a \qquad \qquad \quad a\times b = b \times a \\ \begin{array}{c} \text{The same result is obtained regardless of the order }\\ \text{in which two numbers are added or multiplied.} \end{array} \end{array} \\ \hline \hline \begin{array}{c} \text{Associative} \\ \text{Property} \end{array} & \begin{array}{c} \left(a + b \right) + c = a + \left(b + c \right) \qquad \left( a\times b\right)\times c = a\times \left( b \times c\right) \\ \begin{array}{c} \text{If three numbers are added or multiplied at the same time,} \\ \text{the same result is obtained regardless} \\ \text{of which of them is added or multiplied first.} \end{array} \end{array} \\ \hline \hline \begin{array}{c} \text{Distributive} \\ \text{Property} \end{array} & \begin{array}{c} a\times\left( b + c \right) = a \times b + a \times c \\ \left( b + c \right) \times a = b \times a + c \times a \\ \begin{array}{c} \text{
Simplification of expressions, form the basis} \\ \text{for factoring methods.} \end{array} \end{array} \\ \hline \hline \begin{array}{c} \text{Identity} \\ \text{Property} \end{array} & \begin{array}{c} a + 0 = a \qquad a \times 1 = a \\ \begin{array}{c} \text{If} a \text{ is added to } 0 \text{, it will remain } a \text{, and if it is } \\ \text{multiplied by } 1 \text{, it will also be the result of } a. \end{array} \end{array} \\ \hline \hline \begin{array}{c} \text{Inverse} \\ \text{Property} \end{array} & \begin{array}{c} a + (-a) = 0 \qquad a\times a^{-1} = 1 \\ \begin{array}{c} \text{If } a \text{ is a real number, there is a real number } \\ \text{called the negative} = -a \\ \text{If } a \text{ is not zero, there is a single real} \\ \text{number called the reciprocal } =a^{-1} \end{array} \end{array} \\ \hline \hline \end{array}Irrational Numbers (I)
Irrational numbers are all those numbers that cannot be expressed because their decimal expressions continue indefinitely without presenting any repeating pattern. We can add as many numbers as we can to these numbers, but they will never have a repeating pattern compared to rational numbers.
Examples of irrational numbers
I am sure that you have ever seen the number \pi, let me tell you that it is an irrational number and in the same way there are many more examples such as the following:
\sqrt{2} = 1.414213562...
\sqrt{3} = 1.732050808...
Rational Numbers (Q)
Rational numbers are all those where their decimals end or have a pattern that repeats indefinitely. These rational numbers include the fractions \left( \frac{x}{y} \right) where the numerator (x) and denominator (y) are integers and the denominator is nonzero.
We can perform the basic operations such as adding, subtracting, multiplying or dividing between two rational numbers and we will always obtain another rational number.
Examples of rational numbers
Rational numbers can be any fraction as long as the denominator is different from zero:
\cfrac{1}{4} = 0.25
\cfrac{2}{3} = 0.666 \dots
The number \frac{2}{3} is a rational number simply because it exhibits a repeating pattern to its decimals.
Integer Numbers (Z)
The integers are all those positive natural numbers, the negatives of each natural number and zero. We can add, subtract and multiply and the division can be done as long as the result does not give a rational or irrational number.
Examples of integer numbers
They are simply the numbers that we normally count with plus the negatives of integers:
\dots , -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, \dots
Natural Numbers (N)
The natural numbers are all those that are represented on the number line after zero. We can perform all the basic operations such as addition, subtraction, multiplication and division as long as the result gives another natural number.
Examples of natural numbers
They are simply all those positive integers, not including zero:
1, 2, 3, 4, 5, 6, 7, 8, \dots
4\times 3 = 12
5/5 = 1
Exponents
First we will define what an exponent is: An exponent (n) is a number used to indicate the number of times a factor is multiplied by itself, just as there are subscripts, the exponent is a superscript.
Exponent example
If n is a positive integer, a^{n} means that a is going to be multiplied by itself n times.
a^{n} = a \times a \times a \dots
2^{4} = 2 \times 2 \times 2 \times 2 = 16
11^{2} = 11 \times 11 = 121
Radicals
Let’s define what a radical is: a radical is an expression that is used when a number cannot be simplified by eliminating some n root or some fractional exponent. So we can express a radical in the form of a root to the n or exponent:
\sqrt[n]{a} = a^{\frac{1}{n}}
\sqrt[n]{b^{m}} = b^{\frac{m}{n}}
Examples of radicals
\sqrt[5]{4} = 4^{\frac{1}{5}}
\sqrt[6]{8^{3}} = 8^{\frac{3}{6}}
Operations with integer exponents
We are going to see 5 cases that occur in operations with integer exponents.
Case 1
When two exponents of a common base are multiplied, the result is equal to the base (b) raised to the sum of the two exponents.
b^{n} \times b^{m} = b^{n + m}
Case 2
A base a with an exponent m that is divided by the same base a but with a different exponent n, is equal to the same base raised by the subtraction of the exponent of the base of the numerator minus the exponent of the base of the denominator.
\cfrac{a^{m}}{a^{n}} = a^{m-n}
Case 3
An exponent n raised to another exponent m is equal to the base raised to the product of the two exponents.
\left( a^{n}\right)^{m} = a^{n\times m}
Case 4
The product of two numbers raised to a power n is equal to the product of each number raised to that power.
\left( a\times b\right)^{n} = a^{n} \times b^{n}
Case 5
The quotient of two numbers raised to a power n is equal to the quotient of each number raised to that power.
\left( \cfrac{a}{b} \right)^{n} = \cfrac{a^{n}}{b^{n}}
Thank your for being in this moment with us : )
