Let’s go once with the definition, then we will see some characteristics, then we will mention theorems with their properties of logarithms and finally two examples of logarithms.
Definition of logarithm
The logarithm of a number with a given base is the exponent to which the base must be raised to obtain the number.
We are going to explain this definition a little more. We have that the relationship that exists between the exponential and logarithmic functions is that the logarithms are the inverse function of the exponentials, therefore, if we have an exponential function such as:
y = b^{x}
The logarithm of that function that can also be called as the inverse is:
\log_{b}y = x
But since we are used to handling x as the numbers and y as the function, we write it as follows:
y = \log_{b}x
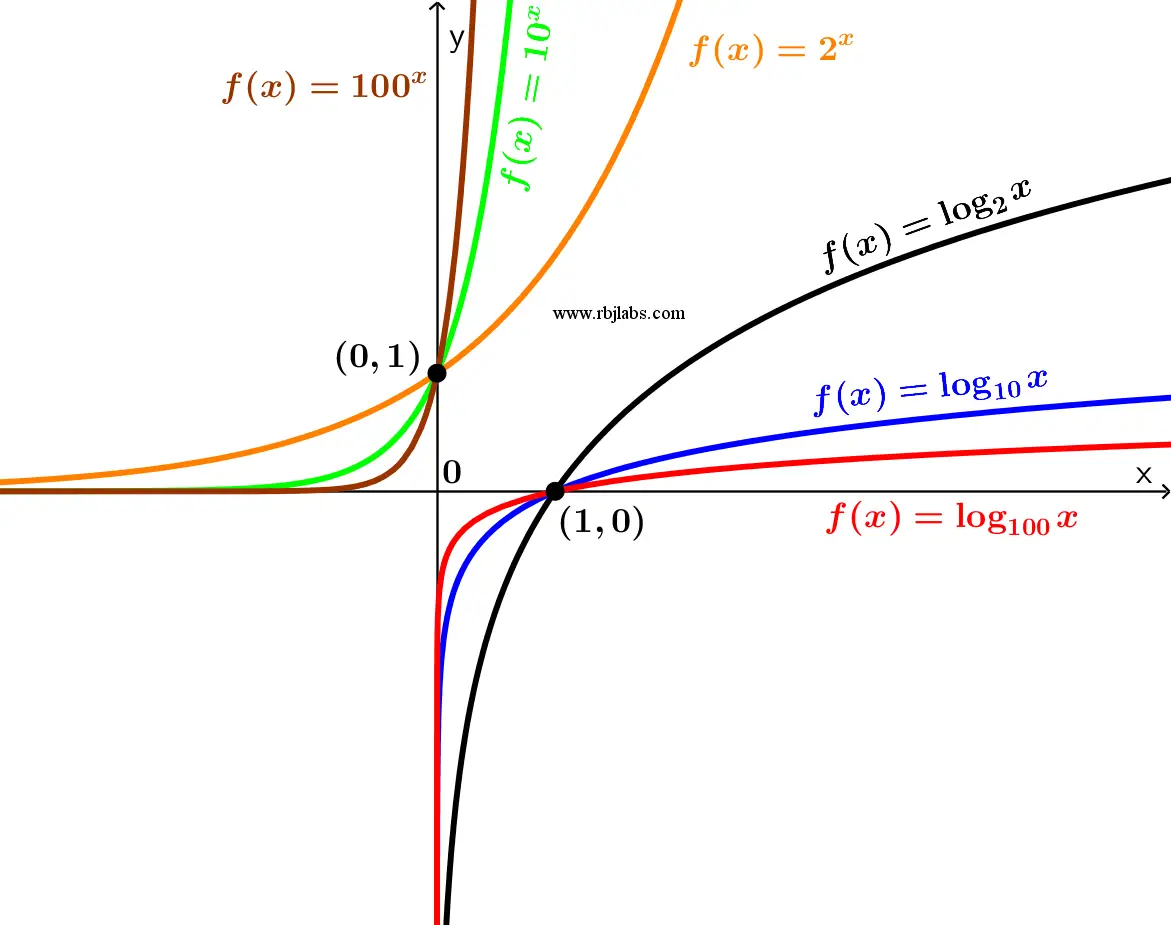
As can be seen in Figure 1, the exponential functions with their respective inverse or logarithmic functions can be appreciated.
Continuing with the explanation, if we have the following expression:
\text{(1)} \quad \quad 6 = 2^{x}
To find the value of x we need to understand that x is between the values of 2 and 3 since 2^{2}=4 and 2^{3} = 8, starting from here we will start testing values to get closer to our value of 6. That is why we have logarithms since logarithms are also exponents. Taking as a representation the following:
\text{(2)} \quad \quad \log_{2}6 = x
Likewise, the only way to find exactly the value of x is by doing many iterations of the expression \text{(1)}, as we had explained, trying values between 2 and 3 until we have a number with many decimals.
This is why the value of x is represented as \log_{2}6 and not as a number with many decimal places. Of course, if you grab your calculator and put \log_{2}6 it will give you 2.5849..., which is an approximate value but very very close to the result since the calculator iterates to give you your answer, only that the calculator can do many iterations in less than a second.
The only way to have the exact value is to do infinite iterations, but that would take an infinity of time. It’s the funny thing about mathematics.
Characteristics of logarithms
Logarithms have many peculiarities as in many subjects in algebra and now I am going to show you those characteristics that logarithms have for when you go to do your homework.
- Only positive numbers have real logarithms. Negative numbers do not exist in the field of logarithms, such logarithms of real numbers are complex numbers and also the logarithm of zero is not defined.
- When a number x increases, its logarithm b also increases. And when x tends to infinity, b does too. So we can write the following:
\underset{x \to \infty} \lim \; \log_{b}x = \infty
- For x < 1, \log_{b} x < 0; for x = 1, \log_{b} x = 0; and for x > 1, \log_{b} x > 0
- When x tends to zero, its logarithm tends to minus infinity, which is written as follows
\underset{ x \to 0} \lim \; \log_{b}x = - \infty
Properties of logarithms
We will see the properties of logarithms in the following theorems, which are the results of transforming four laws of exponents:
- b^{x}\cdot b^{y} = b^{x+y}
- b^{x} \div b^{y} = b^{x-y}
- \left(b^{x} \right)^{n} = b^{nx}
- n\sqrt{b^{x}} = b^{x/n}
Of which we will write the following
M = b^{x} \qquad \text{y} \qquad N=b^{y}
from where:
x = \log_{b}M \qquad \text{y} \qquad y = \log_{b} N
Theorem 1
The logarithm of the product or of the multiplication of two positive numbers is equal to the sum of the logarithms of each number.
\log_{b}MN = \log_{b}M + \log_{b}N
If you have a multiplication number, you can safely separate it as a sum of logarithms.
Theorem 2
The logarithm of the quotient of two positive numbers is equal to the logarithm of the dividend minus the logarithm of the divisor.
\log_{b}\cfrac{M}{N} = \log_{b}M - \log_{b}N
As you can see, if your number is a division, you can pass it to a logarithm subtraction, just remember that it will always be the logarithm of the numerator minus the logarithm of the denominator. Don’t do it backwards because that’s wrong.
Theorem 3
The logarithm of the nth power of a positive number is equal to n times the logarithm of the number.
\log_{b}M^{n} = n\log_{b}M
We know it as lowering the exponent, this is one of the advantages that logarithms give us, that we can lower the exponent that our number has and that it happens by multiplying the whole logarithm.
Theorem 4
The logarithm of the real positive nth root of a positive number is equal to the result of dividing the logarithm of the number by n.
\log_{b}M^{n/a} = \cfrac{n}{a}\log_{b}M = \log_{b}\sqrt[a]{M^{n}}
This results in several properties that logarithms give us:
\log_{b}b = 1
\log_{b}b^{n} = n
b^{\log_{b}N} = N
Theorem 5
The logarithm of a positive number N in the base a, is equal to the logarithm of N in another base b, divided by the logarithm of a in the base b.
\log_{a}N = \frac{\log_{b}N}{\log_{b}a}
Solved Examples of Logarithms
Let’s look at some solved examples of logarithms so that we can better understand all the previous concepts.
Logarithms example 1
Find the value of x from the following expression:
\log_{b}x = \log_{b}2 + 3 \log_{b}2 - \log_{b}4
To start with this exercise of logarithms, we will make all the logarithms are multiplied by 1, what I mean is that we can pass the 3 of the term 3\log_{b}2 as the exponent of the 2:
\log_{b}x = \log_{b}2 + \log_{b}2^{3} - \log_{b}4
The next thing is that we will multiply the numbers of the sum of the logarithms, as our Theorem 1 of logarithms says:
\log_{b}x = \log_{b}2\cdot 2^{3} - \log_{b}4
In this step we can do two things, either multiply the 2 with the 2^{3} and then apply the Theorem 2 of the logarithms or we can first apply the Theorem 2 and then multiply. We will do what we said first:
\log_{b}x = \log_{b}16 - \log_{b}4
\log_{b}x = \log_{b}\frac{16}{4} = \log_{b} 4
And finally based on one of our properties of Theorem 4 that says:
b^{\log_{b}N} = N
We get our result from the value of x:
b^{\log_{b}x}=x \ \ \text{y} \ \ b^{\log_{b}4} = 4
x = 4
Logarithms example 2
In this example we will use logarithms to find the inverse function of the following function:
y = b^{x + 2}
To begin with this exercise, what we will do is apply the following property of our Theorem 4:
\log_{b}b^{n} = n
Where n is equal to x+2, so we will apply a logarithm to the entire expression:
\log_{b}y = \log_{b}b^{x+2}
We will use Theorem 3 to pass the exponent of b by multiplying:
\log_{b}y = \left(x + 2 \right) \log_{b}b
We carry out some simple operations:
\log_{b}y = x\log_{b}b + 2\log_{b}b
Now what we will do is pass our expression 2\log_{b}b on the other side of the equality
\log_{b}y - 2\log_{b}b = x\log_{b}b
And we are almost done, what we will apply now is one of our properties of our Theorem 4 that says:
\log_{b}b=1
Which makes us able to eliminate the logarithm where x is and where 2 is:
\log_{b}y - 2 = x
Ordering the equality we have our result of the inverse function found:
x = \log_{b}y - 2
Thank you for being in this moment with us : )
