Let’s start by representing the point A and the plane ax + by + cz = d:
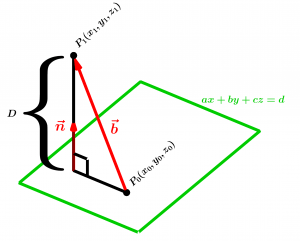P_{1} is a point in the given plane. From the plane we have the point P_{0} and also a vector \vec{b} that defines the segment \overset{\longrightarrow}{P_{0}P_{1}}:
\vec{b} = <x_{1} - x_{0},y_{1} - y_{0},z_{1} - z_{0} >
The distance D of P_{1} to the plane is equal to the absolute value of the scalar projection of \vec{b} on the normal vector \vec{n}:
D = \left| comp_{\vec{n}}\vec{b}\right| = \left| \cfrac{\vec{n}\cdot \vec{b}}{|\vec{n}|} \right|
The above equation is read as the absolute value of the dot product of the normal vector n multiplied by the vector b divided by the absolute value of the normal vector n. Remember that the normal vector n is represented with the coefficients of the unknowns of the plane equation respectively, that means that if the equation of the plane is ax + by + cz = d, then the normal vector is \vec{n} = <a, b, c>. Here is the equation obtained from the operations of the previous equation:
D =\cfrac{a(x_{1} - x_{0}) + b(y_{1} - y_{0}) + c(z_{1} - z_{0})}{\sqrt{a^{2} + b^{2} + c^{2}}}
Multiplying the parentheses is as follows:
D =\cfrac{ax_{1} - ax_{0} + by_{1} - by_{0} + cz_{1} - cz_{0}}{\sqrt{a^{2} + b^{2} + c^{2}}}
We sort all the unknowns with sub-index 1 together and the unknowns with sub-index 0 together:
D =\cfrac{ax_{1} + by_{1} + cz_{1} - ax_{0} - by_{0} - cz_{0}}{\sqrt{a^{2} + b^{2} + c^{2}}}
We factor the negative and it looks like this:
D =\cfrac{ax_{1} + by_{1} + cz_{1} - (ax_{0} + by_{0} + cz_{0})}{\sqrt{a^{2} + b^{2} + c^{2}}}
But as the general equation of the plane is:
a(x - x_{0}) + b(y - y_{0}) + c(z - z_{0}) = 0
ax - ax_{0} + by - by_{0} + cz - cz_{0} = 0
ax + by + cz = ax_{0} + by_{0} + cz_{0}
Note that d = ax_{0} + by_{0} + cz_{0}, then the equation of the distance from the point to the plane can be written finally as follows:
D = \cfrac{ax_{1} + by_{1} + cz_{1} - d}{\sqrt{a^{2} + b^{2} + c^{2}}}
Exercise of distance between a point and a plane
Find the distance from point (3,-2,7) to the plane 4x-6y+z=5
It is not necessary to graph the point and the plane, but we are going to do it:
The exercise is solved using a simple formula, we have P_{1} which is:
P_{1} = (3,-2,7)
The normal vector is the one that will give us the values of a, b and c; but the normal vector are the coefficients of the unknowns of the plane equation respectively:
\begin{array}{c c c c c c} \vec{n} & = < & 4, & -6, & 1 & >\\ & & a & b & c & \end{array}With our point P_{1}, our normal vector and d, we simply substitute in the formula:
D = \cfrac{(4)(3) + (-6)(-2) + (1)(7) - 5}{\sqrt{(4)^{2} + (-6)^{2} + (1)^{2}}}
And we grab a calculator to make the operations easier to finally have our distance between the point P_{1} and the plane:
D = \cfrac{26\sqrt{53}}{53} \ \text{u}
The \text{u} means “units”.
Thank you for being at this moment with us : )