Welcome back! In this wonderful post we will learn to solve the Square-1 and you will have no choice but to learn various algorithms.
We are going to go step by step from when you have the Square-1 completely amorphous until the colors are in their resolved state, the steps we will do are the following:
- Return the cube to its cubic form
- We will place the white corners on their corresponding face and consequently the yellow ones
- We will swap the corners to accommodate them
- We will place the edges on its white face and the yellow ones on its yellow face
- We will permute the edges of each face
I remind you that the algorithms that we will see consist of numbers, it is not like the traditional 3×3 Rubik’s cube.
These algorithms are like coordinates, but it’s very easy to understand, let me explain: the algorithms consist of slashes / and parentheses with two numbers (x,y).
What the diagonals represent is that you are going to turn the right face of the cube in half, in the cross section of Square-1, a 180° turn. And what the coordinates mean is that x you are going to rotate the upper face and y the lower face. Now, what needs to be clarified is that you will have numbers, when you have a positive number you will rotate the faces clockwise, and if you have a negative number, you will rotate it counterclockwise.
Now, since you will have numbers in the coordinates, you just have to remember that each edge has a value of 1 and each corner has a value of 2. Looking at it another way: the small pieces have the small value and the large pieces have the large value, 1 and 2 respectively. Also keep in mind that when we see the value of zero it means that we will leave that face still. So if you see an algorithm like this:
/(3,3)/(0,3)/(1,1)/(-1,-4)/(-3,-3)
- We will do: cut 180°
- Upper face: clockwise rotation 1 edge and 1 corner
- Lower face: clockwise rotation 1 edge and 1 corner
- Cut 180°
- Upper face: nothing
- Lower face: clockwise rotation 1 edge and 1 corner
- Cut 180°
- Upper face: clockwise rotation 1 edge
- Lower face: clockwise rotation 1 edge
- Cut 180°
- Upper face: counterclockwise rotation 1 edge
- Bottom face: counterclockwise rotation 1 edge, 1 corner and 1 edge
- Cut 180°
- Upper face: counterclockwise rotation 1 edge and 1 corner
- Lower face: counterclockwise rotation 1 edge and 1 corner
And with that we already have our first algorithm, and once you practice it, the execution of the algorithms will be much faster. It should be noted that when you have a number 2 in the algorithm it will not necessarily always be a corner, since the edges have a value of 1 then that 2 in the algorithm can also mean moving two edges.
What you have to do is move the number of units that the algorithm asks for and since the edge is worth one and the corner is worth two, you can have many combinations.
Let’s start!
Return Square-1 to its cubic form
Since this step is quite intuitive, I’ll explain the part where we usually get stuck when returning to its cubic shape. What we will do is bring all the edges to the upper face, forming the following shape:

But the vast majority of the time when we are moving the edges to build the shape of Figure 1, we get the following shape:

What we will do is apply the following algorithm grabbing the cube as shown in Figure 2.
/(2,0)/(3,0)/(-1,0)/(-4,0)/
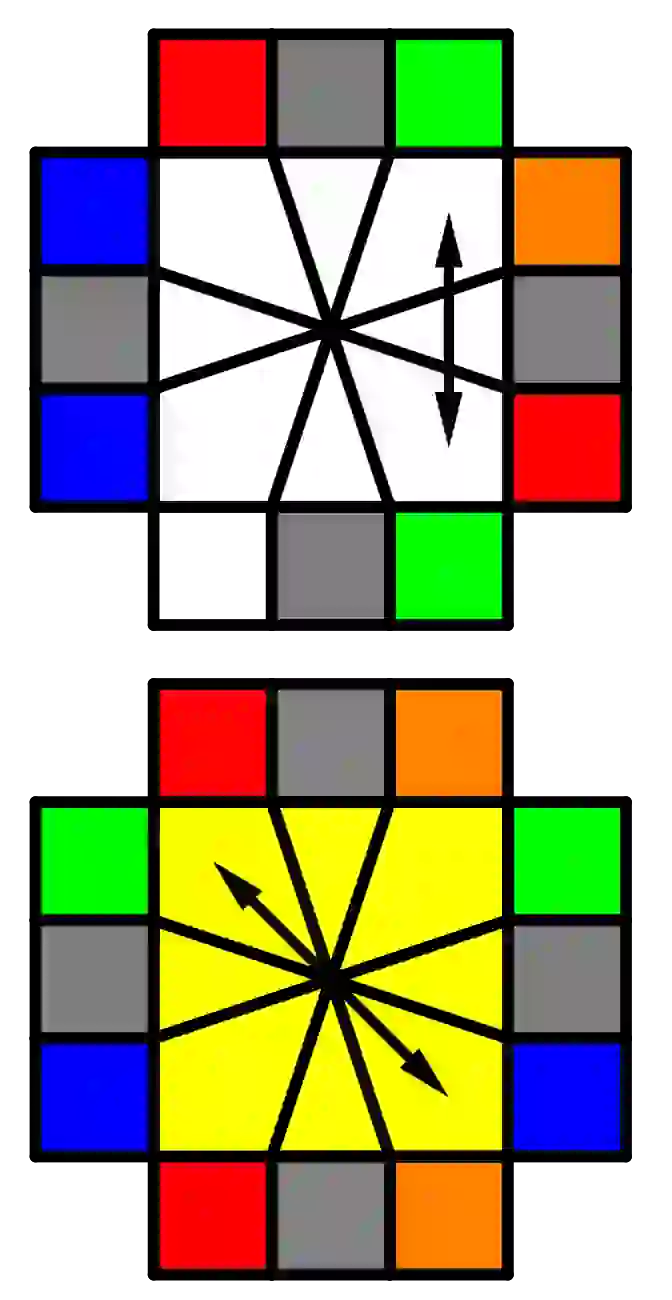
And now that we have the shape of Figure 1 we will apply the following algorithm grabbing it as shown in Figure 1 itself:
/(-4,-2)/(-1,-2)/(-3,-3)/
Done, you already have the cubic shape!
Sometimes when we return to the cubic shape the middle layer does not remain in the cubic shape as shown in Figure 3:

Then apply the following algorithm:
/(-6,0)/(-6,0)/
Being very honest, I do not recommend that you waste time applying this last algorithm because we do not know if when we finish arranging the whole cube, you will end up with that highlighted part of Figure 3 again. You may solve everything and you will be left as shown in Figure 4 where all the colors are accommodated but the part in the middle does not remain, in this case you do apply the previous algorithm.

That’s why you solve both sides of Square-1 first and worry about the middle of the cube at the end.
Next step!
Accommodate corners of each opposite face of Square-1
In this step we’ll let you think a bit because we think placing the 4 white corners on one side and the yellow ones on the other is pretty intuitive. If you find something complicated, write us in the comments that you want us to put how to accommodate the corners on their respective faces.
We will swap corners of each face of Square-1
Once we have arranged the corners of Square-1, we need to swap them to place them in their position, then what I will do is put some algorithms that will help you swap the edges, whether they are in an adjacent position or in a opposite position
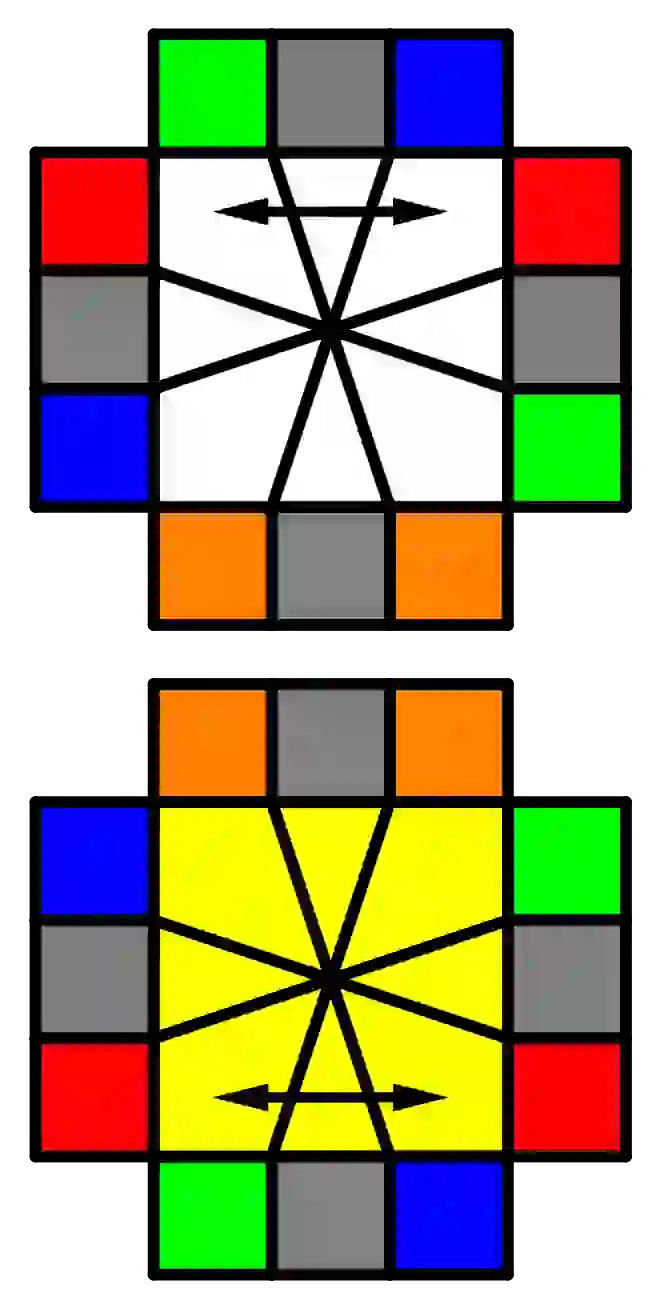
 | /(3,-3)/(-3,0)/(0,3)/(0,-3)/(0,3)/ | 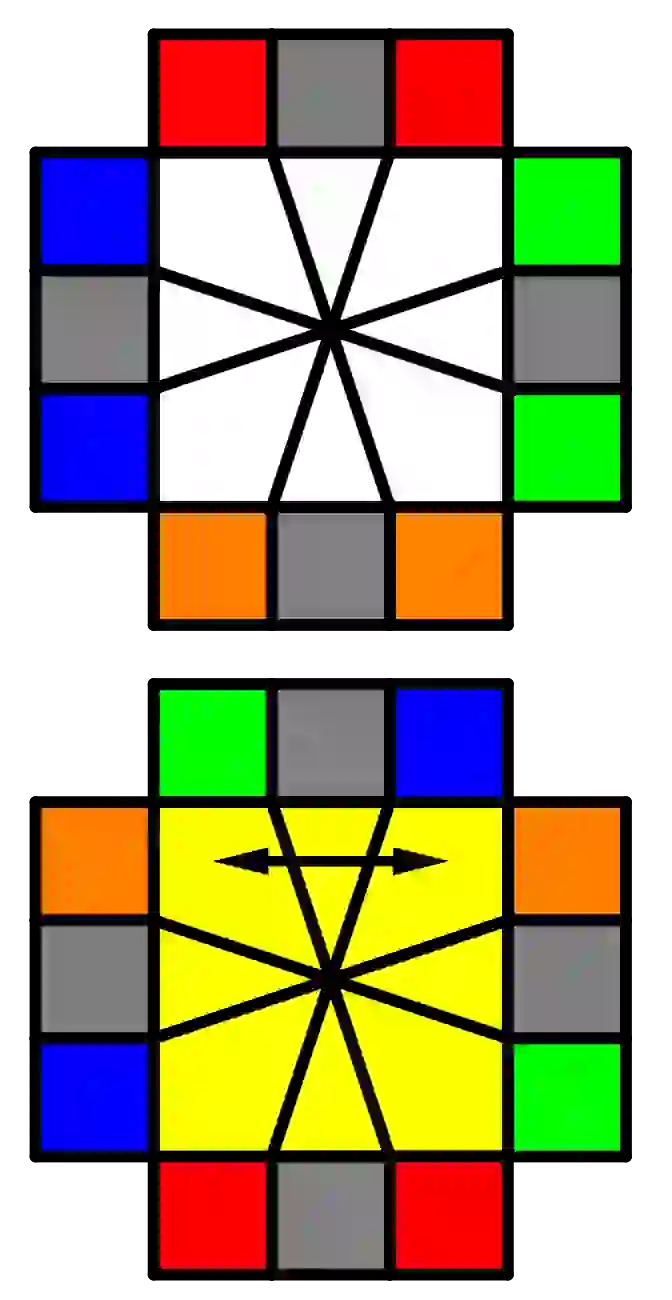 | /(3,-3)/(0,3)/(-3,0)/(3,0)/(-3,0)/ |
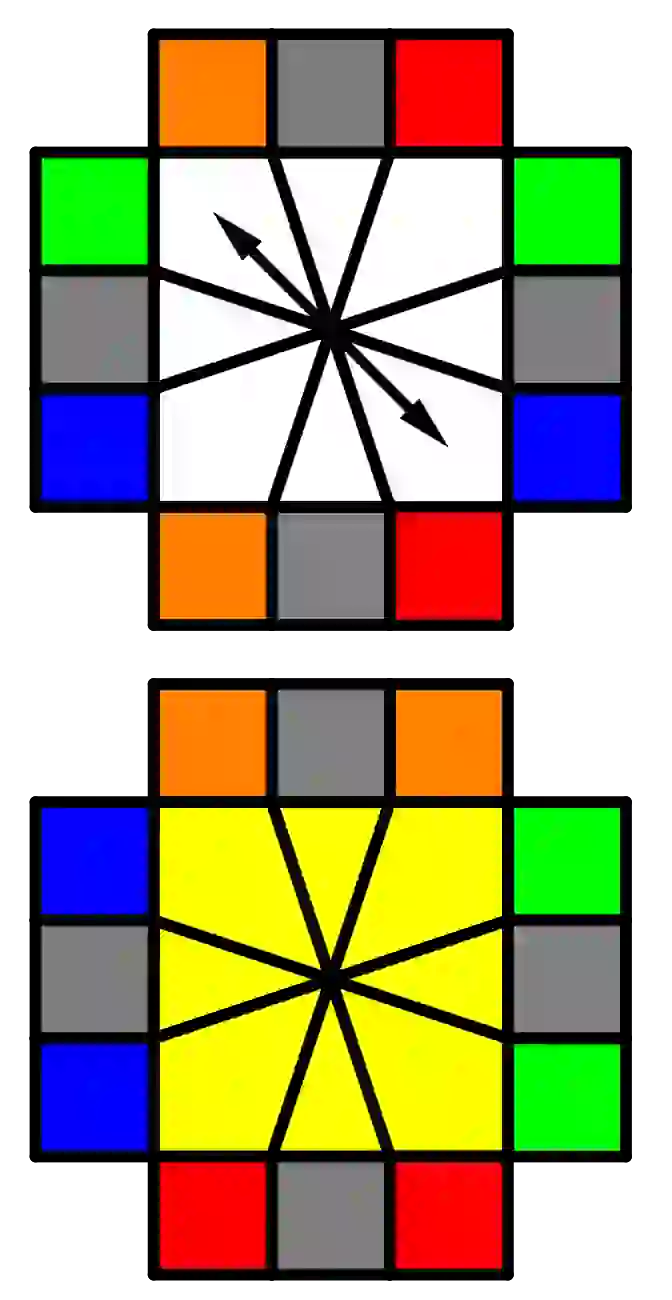 | /(-3,-3)/(3,0)/(-3,-3)/(3,0)/(-3,-3)/ | 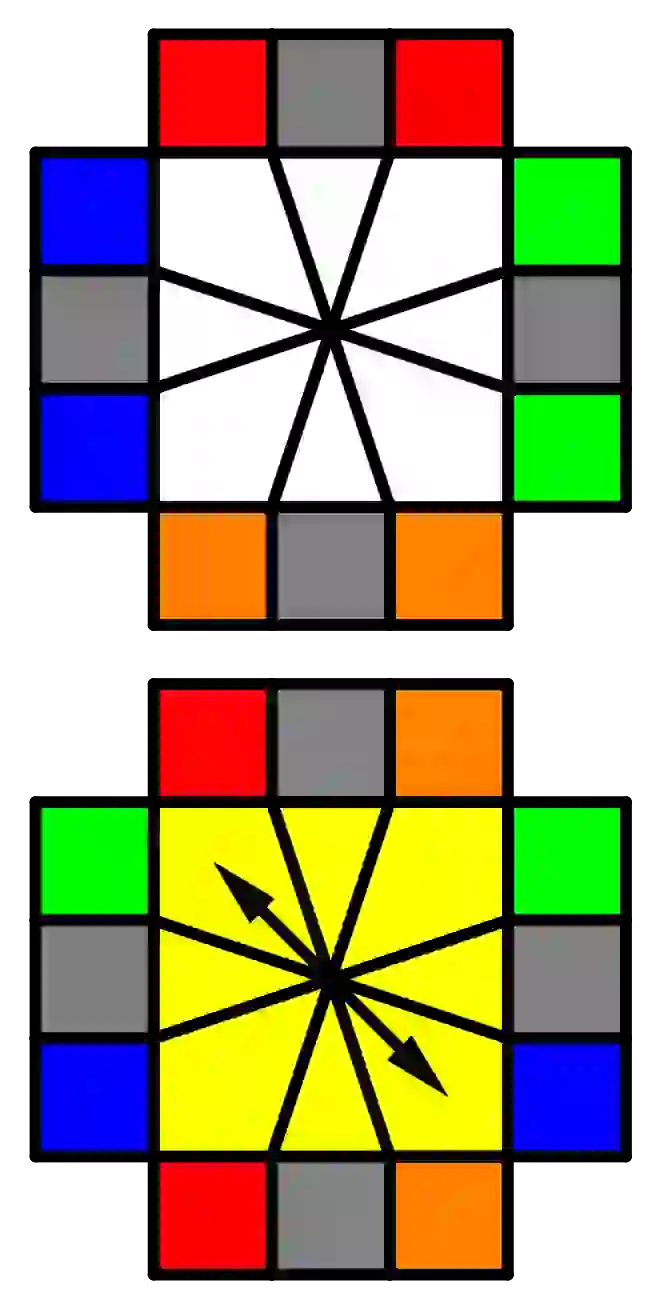 | /(-3,-3)/(0,-3)/(-3,-3)/(0,-3)/(-3,-3)/ |
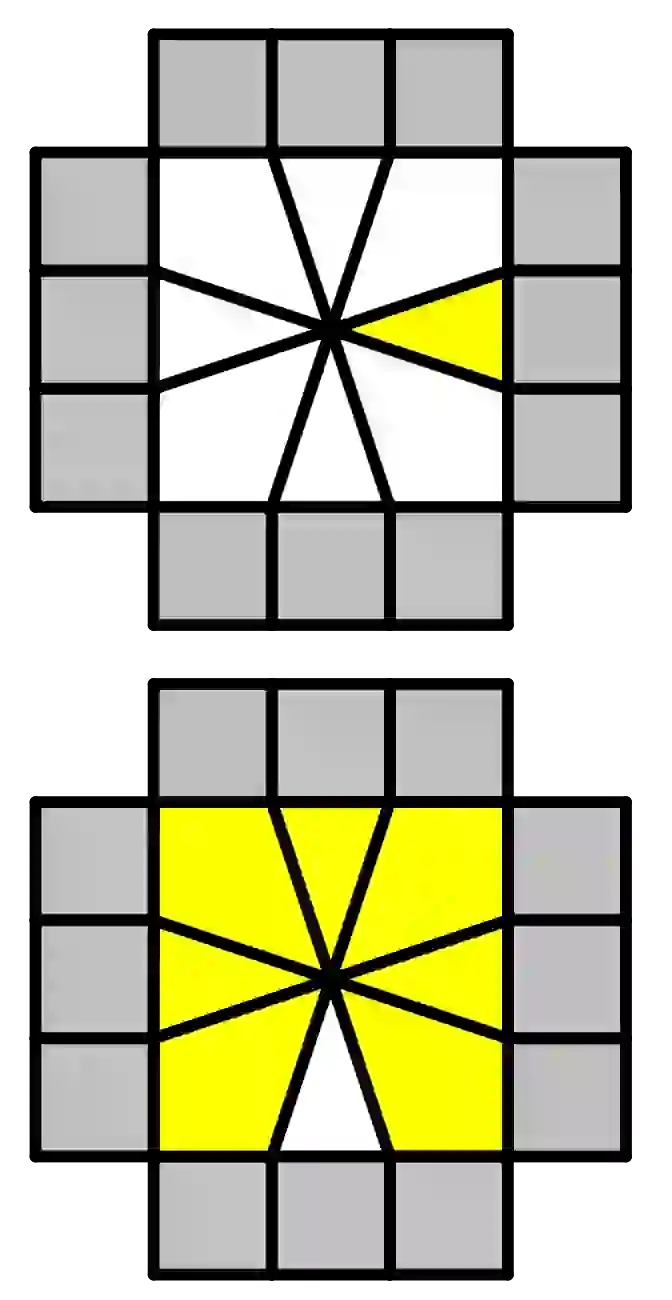
 | /(3,0)/(-3,-3)/(0,3)/ | 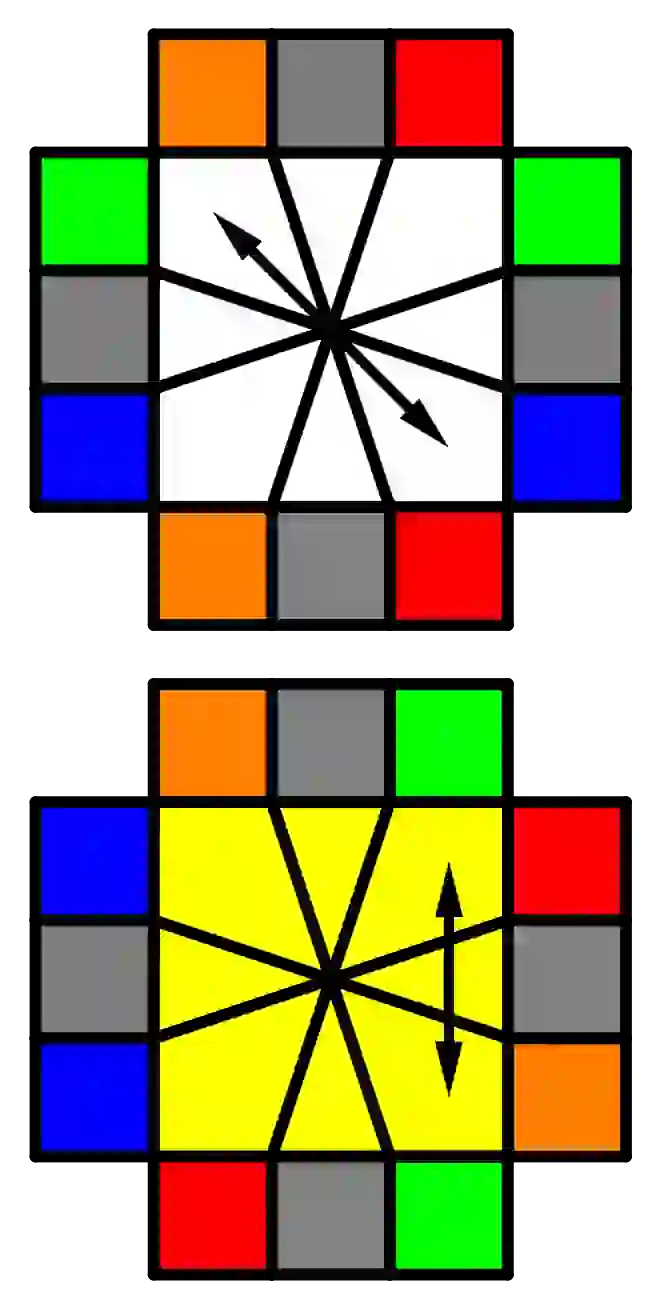 | /(3,0)/(-3,0)/(3,0)/(-3,0)/ |
 | /(0,3)/(0,-3)/(0,3)/(0,-3)/ |
I put a few more algorithms in case you want to learn them to swap the two faces with the same algorithm, but you can calmly swap face by face. Everything will depend on the situation that is presented to you.
Accommodate edges of each face of Square-1
To accommodate the edges in the easiest way is to apply 3 very useful algorithms, I present them below. The algorithm to accommodate 3 edges is a variation that what it does is place 2 edges of each face and that remaining edge is solved with the algorithm to accommodate one edge, you will see it when you practice them.
 | (1,0)/(3,0)/(3,0)/(-1,-1)/(-2,1)/(-3,0)/ | 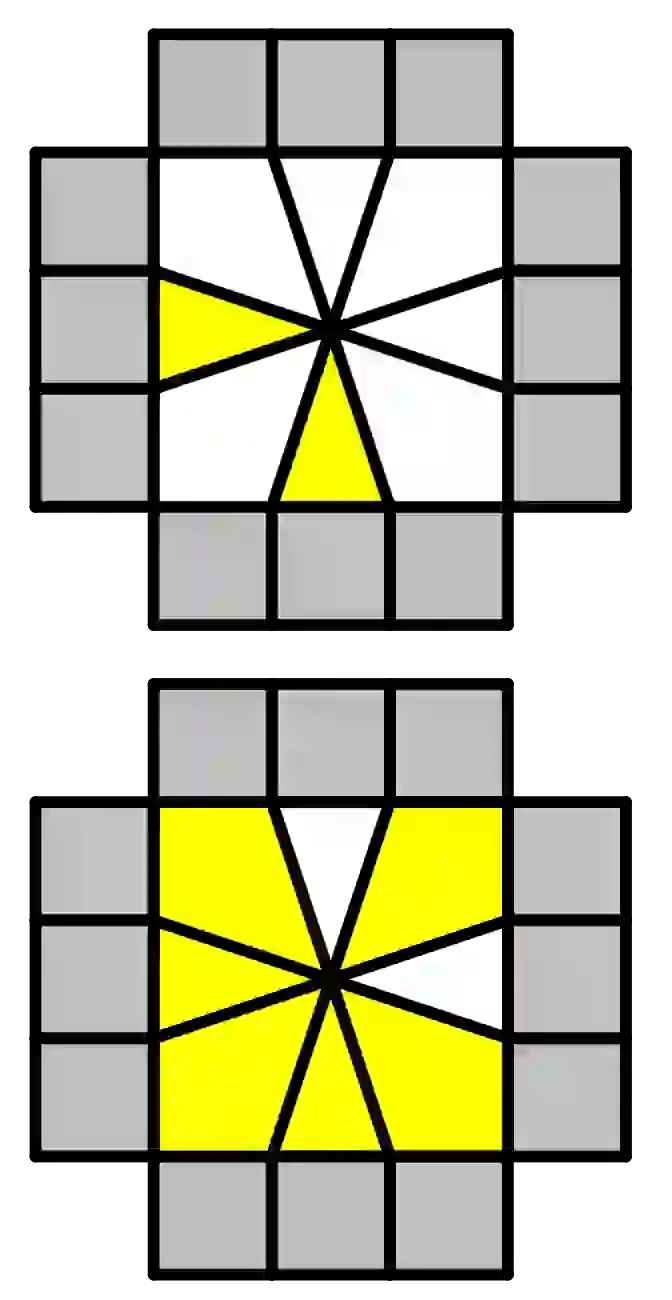 | (1,0)/(3,0)/(-1,-1)/(-3,0)/(0,1) |
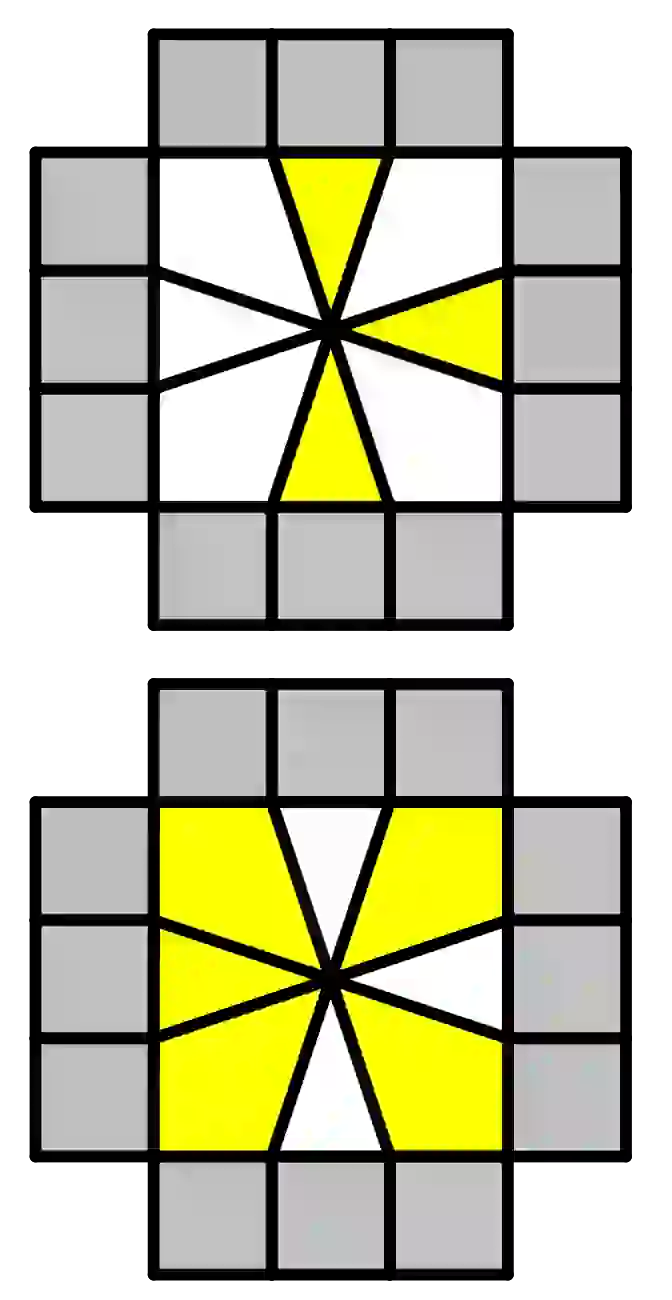 | (1,0)/(-1,-1)/(0,4) Next we make the algorithm to accommodate a single edge |
We will swap edges of each face of Square-1
Here comes the good part, this is the interesting part where you have to put a little more head to learn various algorithms, there is no other. Honestly, by learning 2 algorithms for the upper face and 2 for the lower face, you already build the cube completely, that is, learn 4 algorithms. But it is very impractical when it comes to wanting speed, that is why I will give you the algorithms that we consider are the ones you need for the moment.
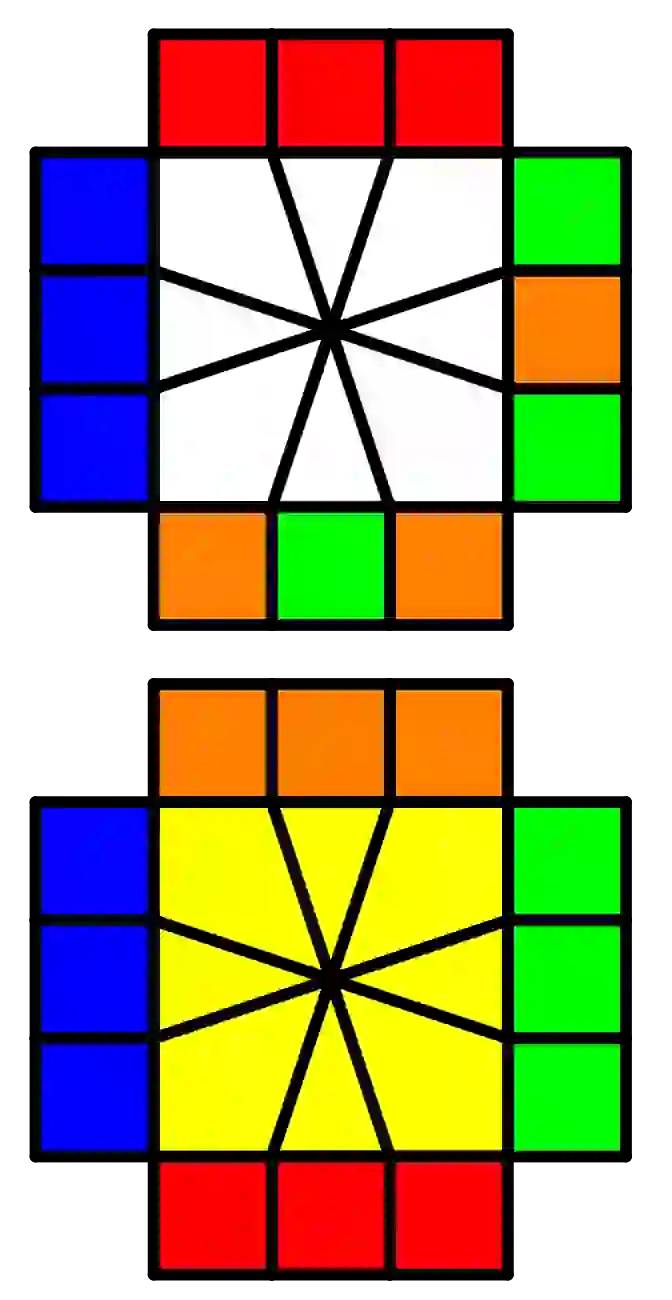 | /(-3,0)/(0,3)/(0,-3)/(0,3)/(2,0)/(0,2)/ (-2,0)/(4,0)/(0-2,)/(0,2)/(-1,4)/(0,-3)/ (0,3) | 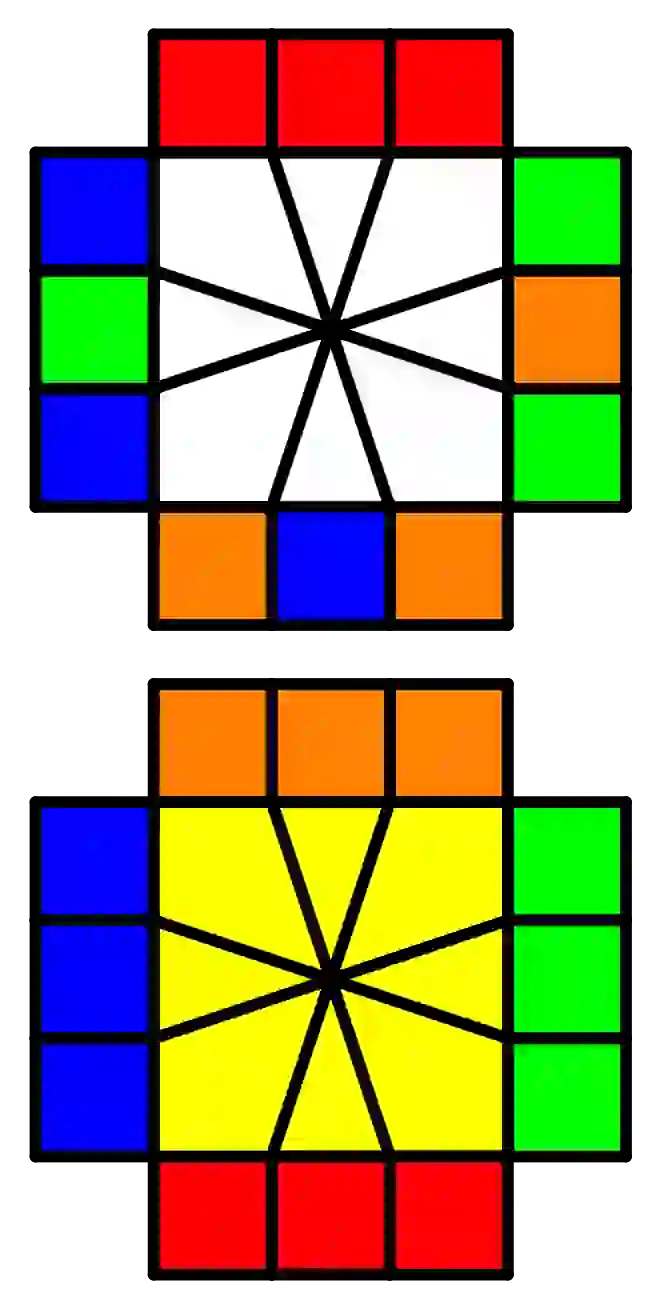 | /(0,3)/(1,0)/(-3,0)/(-1,0)/(0,-3)/(1,0)/ (3,0)/(-1,0) |
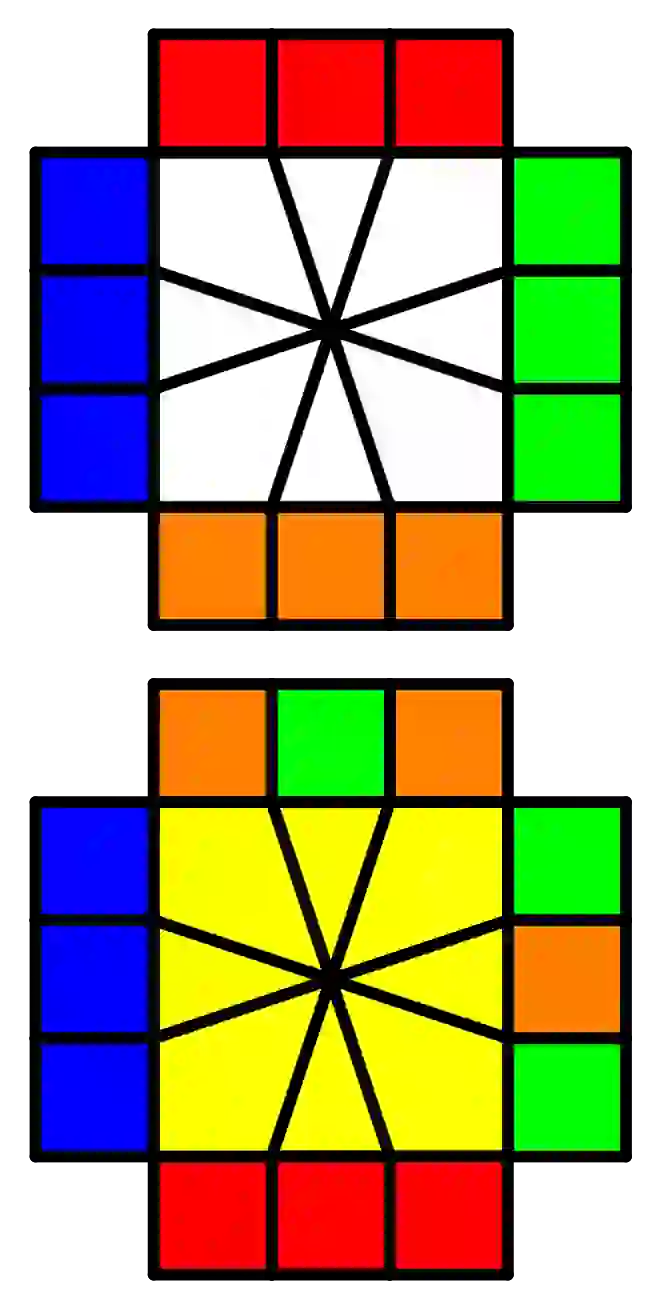 | /(0,3)/(-3,0)/(3,0)/(-3,0)/(0,-2)/(-2,0)/ (0,2)/(0,-4)/(2,0)/(-2,0)/(-4,1)/(3,0)/ (-3,0) |  | /(0,-3)/(0,-1)/(3,0)/(0,1)/(0,3)/(0,-1)/ (-3,0)/(0,1) |
The parity algorithms will only help you when you cannot identify a permutation type U, Z or H, that means that it has parity and it must be corrected. When you already manage to identify a type U, Z or H permutation is when you will apply the type U algorithm since this type U permutation helps you to solve the type Z and H permutation, it is like the basic method in the 3×3 rubik’s cube. Will be good in the future if you learn type Z and H permutation of the Square-1.
With these algorithms you can easily solve Square-1. If you have any recommendations for this little tutorial, let us know by writing your opinion in the comment box.
Thank you for being in this moment with us :)
