Simple explanation of what the Venn Diagram is. Basic operations of the sets represented with Venn diagrams. Examples with Venn diagrams and finally we will see important counting formulas! Very cool slates are already used to perform these types of exercises in a more practical and visible way.
What is a Venn Diagram?
Simple, it is the graphic representation of the sets.
Basic operations of the sets
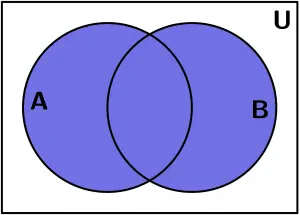
Union (\cup)
It is the set of all the elements that belong to A or B. That is to say:
A \cup B = \{ x:x \in A\lor x \in B\}
A\cup B
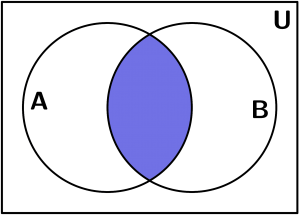
Intersection (\cap)
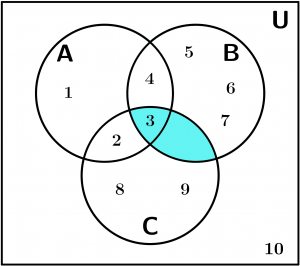
It is the set of elements that belong to [katexs]A[/katex] and B. It means that only the part shared by the sets remains:
A \cap B = \{ x:x \in A \land x \in B\}
A \cap B
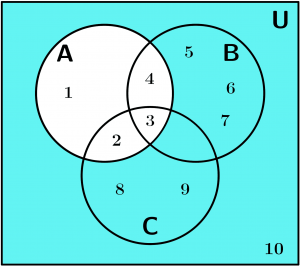
Complement (^{\text{C}})
It is the set of elements that belong to the universe that are not part of A . In other words:
A^{\text{C}} = \{ x:x\in U, x \notin A\}
A^{\text{C}}
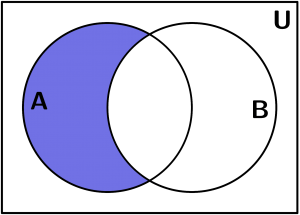
Difference (-)
Is the set that is generated by removing the elements present in the second set:
A- B = \{ x:x \in A, x \notin B\}
A- B
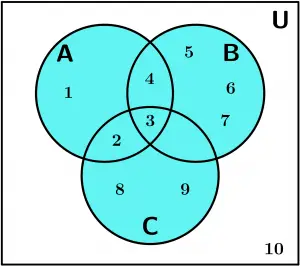
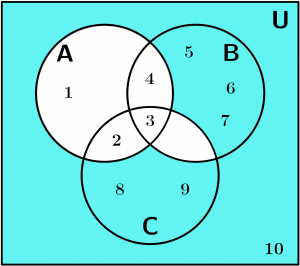
Example of sets with Venn diagrams
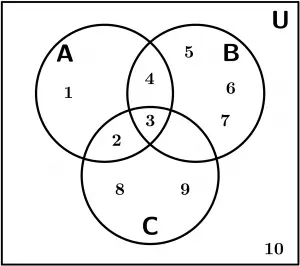
Suppose that the Universe is defined in the following way:
U = \{ 1,2,3,4,5,6,7,8,9,10\}
And the following sets are delimited:
A = \{ 1,2,3,4\}, \ B = \{ 3,4,5,6,7\}, \ C = \{ 2,3, 8,9\}
The Venn diagram is represented as follows:
First example
Represents the union of the set A with the set B and the union of the set B with the set C:
A \cup B \cup C
That means we will have the following numbers:
\{ 1,2,3,4,5,6,7,8,9\}
Now to represent them in the venn diagram:
A \cup B \cup C
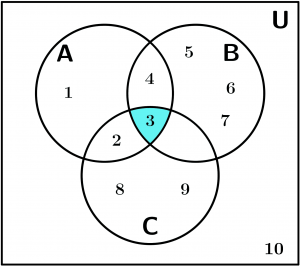
Second Example
Represent the intersection of the set A with the set B and the intersection of the set B with the set C:
A \cap B \cap C
That means we’ll have the number that the three sets have in common:
\{ 3\}
A \cap B \cap C
Third example
Represents the complement of the set A minus the intersection of the set B with the set C:
A^{\text{C}} - (B \cap C)
It is important to do the steps in order:
- The parentheses are prioritized, so first B \cap C is done:
B \cap C
2. Then the A complement is drawn:
A^{\text{C}}
3. Finally the difference is made A^{\text{C}} - (B \cap C):
A^{\text{C}}-(B \cap C)
Result:
\{ 5,6,7,8,9,10\}
Counting formulas
If n(A), n(B) and n(C) are the number of elements that make up the sets A, B and C respectively, then:
- n(A \cup B) = n(A) + n(B) - n(A \cap B)
- n(A - B)=n(A) - n(A \cap B)
- n(A^{\text{C}}) = n(U) - n(A)
- n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(A \cap C) - n(B \cap C) + n(A \cap B \cap C)
Thank you for being at this moment with us : )