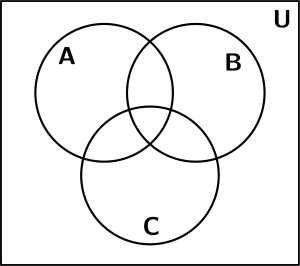
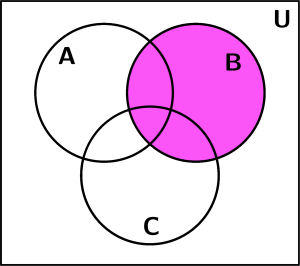
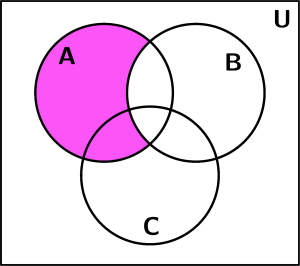
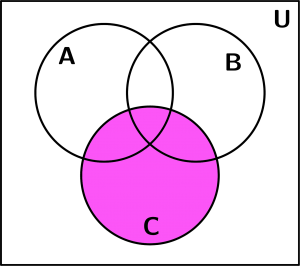
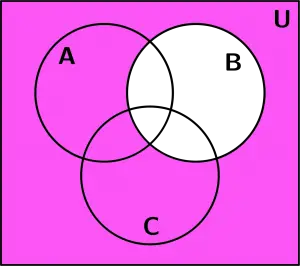
Let’s see 3 examples of sets with Venn diagrams. We will use examples of 3 sets, the set A, the set B and the set C and our base figure with which we will represent the examples of sets with venn diagrams is the next:
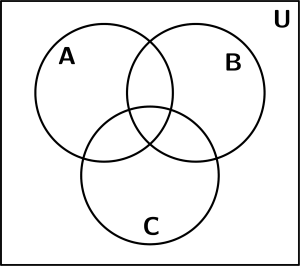
First example of sets with Venn diagrams
Our first example of sets is: A \cap (B \cup C)^{\text {C}}
Let’s start with the parentheses, we will take B and graphically represent how it would looks in a Venn diagram:
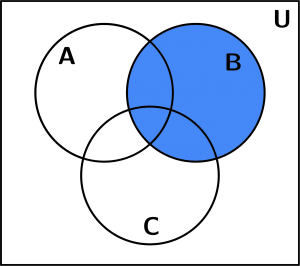
Set B
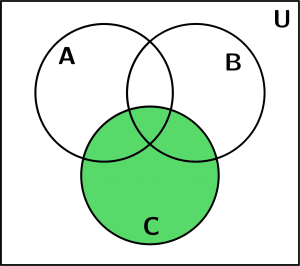
Graphically represent the set C:
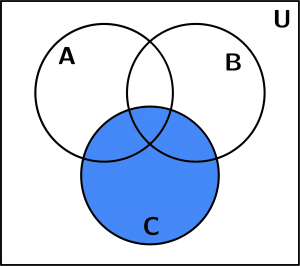
Set C
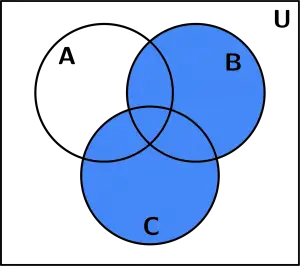
We made the union of the set B with the set C. (B \cup C):
(B \cup C)
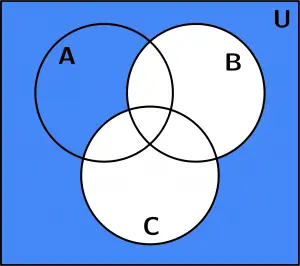
Then the complement that has the parentheses was made. (B \cup C)^{\text{C}}
(B \cup C)^{\text{C}}
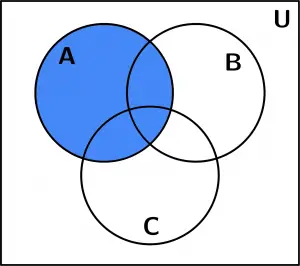
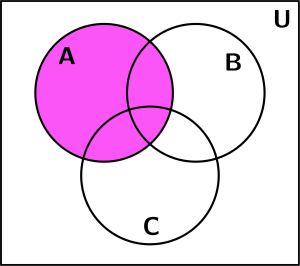
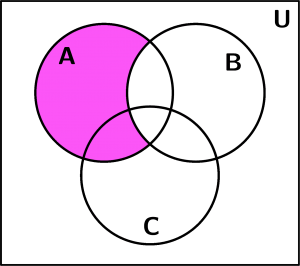
Then we graph the area that occupies only the set A to have it more visually:
Set A
Finally, the intersection indicated in the example was made, so the answer is:
A \cap (B \cup C)^{\text{C}}
Second example of Venn diagrams
Our second example is: C \cup (A^{\text{C}}\cap A)
Now, as we did in the previous example, we start with what is inside the parentheses, identifying each area that says the example statement.
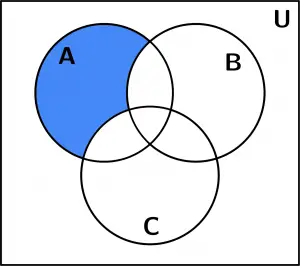
We draw the set A:
Set A
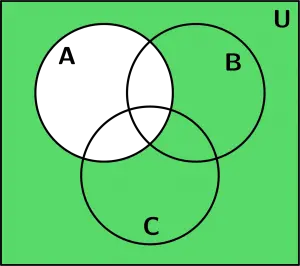
The A complement would looks like this:
A^{\text{C}}
Then the intersection (A^{\text{C}} \cap A) was made:
(A^{\text{C}} \cap A)
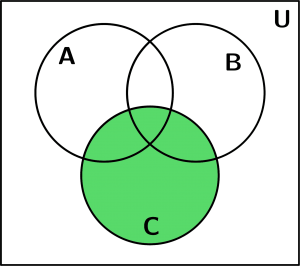
Than the set C was drawn:
Set C
And finally to arrive at the result, the union of C was made with (A^{\text{C}} \cap A), which was observed that the result is the same set of C:
C \cup (A^{\text{C}} \cap A)
Third example with Venn diagrams
The third example of sets with Venn diagrams is: (A - B) \cap (C \cup B^{\text{C}})
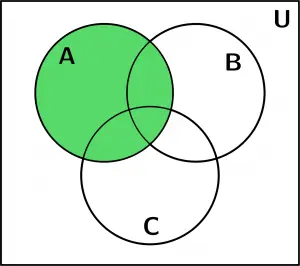
Beginning with the resolution of the exercise, the A and B sets were first drawn:
Set $A$
Set $B$
And then the difference A - B was made:
A-B
After proceeding to make the inside of the other parenthesis, first drawing the set C and then the complement of the set B:
Set $C$
$B^{\text{C}}$
Finally, to arrive at the result, the intersection that says the example was made, the result would be:
(A - B) \cap (C \cup B^{\text{C}})
Thank you for being with us in this beautiful moment of your life : )