Set concept
It is a group of people, animals, or objects depending on their characteristics. One set could be dogs, another the cats. Another set can be the objects of color blue. The possibilities are huge for establishing sets.
Set definition
Collection that have a characteristic in common, people, things, animals, ideas or objects, called elements. For example:
- The days of the week.
- Months of the year.
- The prime numbers.
- The even numbers.
Cardinality of a set
Number of elements that make up a set and is denoted N(\ ). Where N is the set and inside the parentheses is the number of elements that this set contains. The months of the year would be represented as:
A(12)
Where A represents the set “Months of the year” and the number 12 is the number of months.
Finite set
When it is possible to determine the exact number of elements that a set has. As:
- The days of the month of January.
- The number of planets in our Solar System.
Infinite set
When it is not possible to determine the exact number of elements that a set has. As:
- Natural numbers.
- The number of points in a line.
Determination of a set according to its expression
Sets can be named or written in the following ways.
Sets by extension or enumerative
When its elements are explicitly written.
- A=\{\text{blue, white, red, yellow} \}
- B=\{\text{small, big, middle} \}
Sets by comprehension
When describing the characteristics of the elements that belong to the set and it is necessary to establish the relationship of the objects, things or people that make it up. When we name a set for understanding, we usually use symbologies. Some of them are the following:
| Symbol | Meaning |
| \in | element of |
| \notin | not element of |
| = | equal |
| \ne | different |
| < | less than |
| > | greater than |
| \le | less than or equal to |
| \ge | greater than or equal to |
| | | such that |
| R | Real number |
| Q | Rational number |
| Z | Integer number |
To work with sets by comprehension it is necessary to know the meaning of certain mathematical symbols. Let’s see the following example:
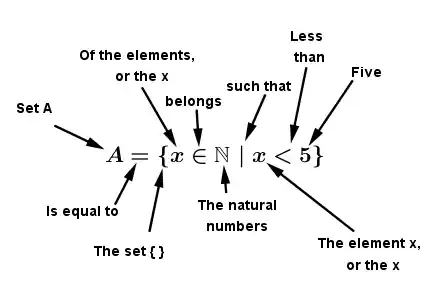 So A = \{ x\in \mathbb{N} \ | \ x < 5 \} is read: “Set A is equal to the set of all numbers that belong to the natural numbers, such that those numbers are less than five.“
So A = \{ x\in \mathbb{N} \ | \ x < 5 \} is read: “Set A is equal to the set of all numbers that belong to the natural numbers, such that those numbers are less than five.“
| Comprehension | Extension | Reading |
| A = \{ x\in \mathbb{Z} | x \ge 9 \} | A=\{ 9, 10, 11, \dots \} | The set A is equal to the set of integers such that x is greater than or equal to 9 |
| B = \{ x \in \mathbb{Z} | 1 < x < 6 \} | B = \{ 2, 3, 4, 5\} | The set B is equal to the set of integers such that x is greater than 1 and less than 6 |
Set classes
There are different sets according to the characteristics they present.
Universal set
They are defined as the totality of elements that have a common general characteristic, denoted by the symbol U. An example can be:
- U = The library books.
- U = The houses of the city.
Empty or null set
It is the set that lacks or has no element, represented as \varnothing.
- \varnothing = People older than 400 years.
- \varnothing = Living dinosaurs that exist today.
Equivalent sets
Two sets are equivalent when the two sets have the same number of elements and at the same time can establish a correspondence with each other. For example:
- Students in a classroom
- Chairs in a classroom.
Assuming that the number of students in a classroom is also the same as the number of chairs in the same classroom.
Equal sets
Two sets are equal if and only if they have the same elements regardless of the order in which they are found:
- A = \{ \text{a, e, i, o, u}\}
- B= \{ \text{i, u, a, o, e}\}
Subsets
A set B is a subset of A if all elements of B belong to A. If the condition is met, then B is said to be a subset of A and is denoted as B\subset A
- A = the students of a school.
- B = the students of the soccer team of the same school.
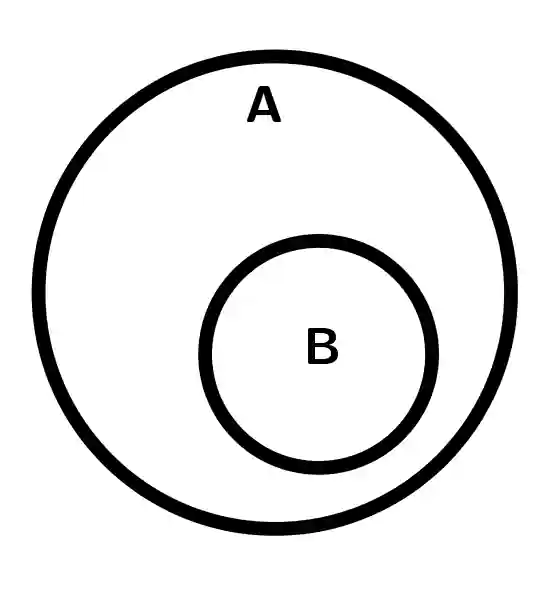 | 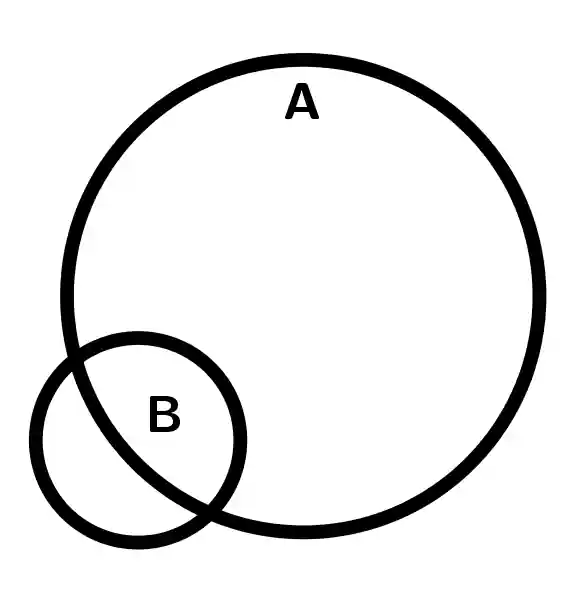 | 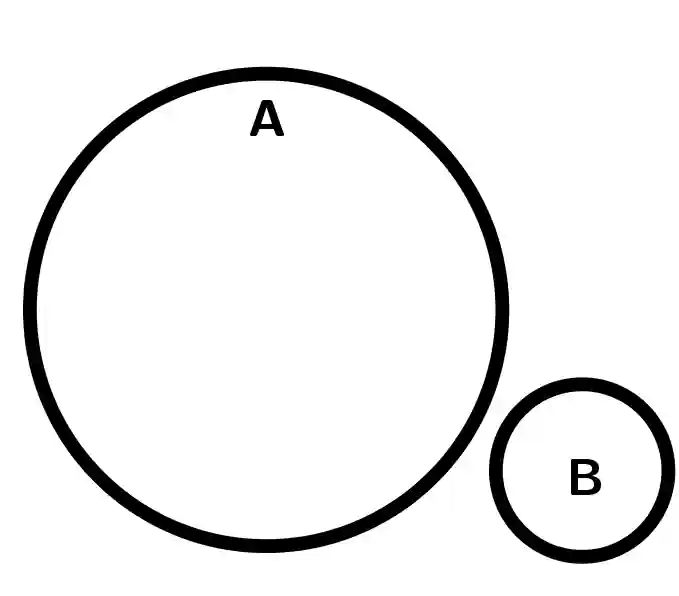 |
| B\subset A | B\not\subset A | B\not\subset A |
| A\not\subset B | A\not\subset B | A\not\subset B Are different sets |
Venn-Euler Diagram
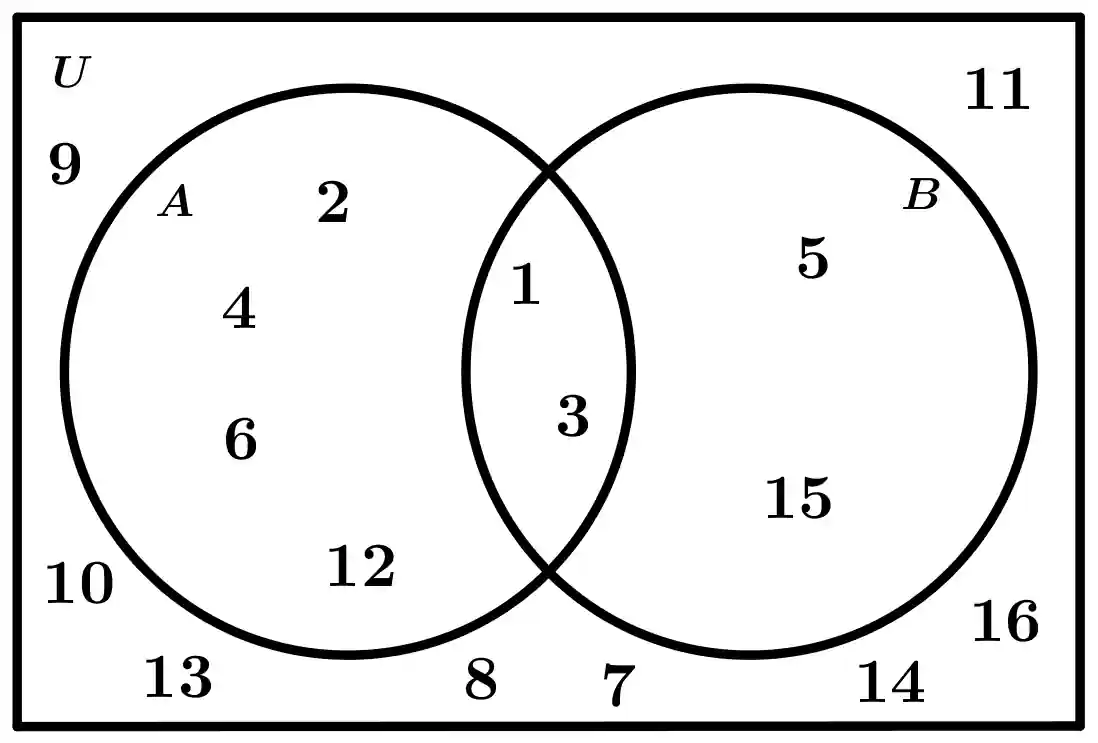
Both the set A and the set B are uniquely defined by the elements that lie inside each circle. It means:
- A = \{ 1, 2, 3, 4, 6, 12\}
- B = \{ 1, 3, 5, 15\}
While the Universe U is made up of all the elements that are in the rectangle, that is, by all those that are inside and outside the circles:
- U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16\}
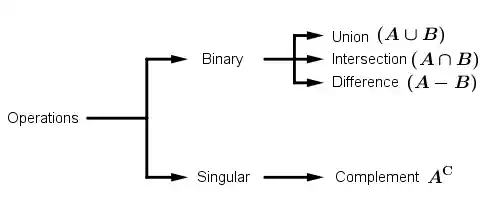
Set operations
Some of the operations that we will see, such as union, intersection, difference, and complement, are classified as binary or singular, as shown in the following example.
Union of sets
The union of the sets A and B, is the set formed by all the elements of A and all the elements of B gathered in one and without repeating them. If they have common elements, they will only be written once to the new set.
The notation used for this operation is A\cup B and is defined as:
A\cup B = \{ x / x \in A \ \text{ó} \ x \in B \}
Union example. Let the sets be formed by:
A = \{ \text{Divisors of } 12 \} = \{ 1, 2, 3, 4, 6, 12\}
B = \{ \text{Divisors of } 15 \} = \{ 1, 3, 5, 15\}
U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16\}
So we have that the union of A with B is:
A \cup B = \{ 1, 2, 3, 4, 5, 6, 12, 15\}
Intersection of sets
The intersection of the sets A and B is the set that is made up of the common elements of the given sets.
The notation that represents it is A \cap B and it is defined as:
A\cap B = \{ x / x \in A \ \text{y} \ x \in B\}
Using the sets A and B from the previous example, we have the intersection:
A\cap B = \{ 1, 3 \}
Set difference
The difference between the sets A and B is the new set that is formed with the elements that belong to the set A by removing the elements that belong to the set B or vice versa. The notation for this operation is A-B or B-A and is defined as:
A-B = \{ x / x \in A \ \text{ and } \ x \notin B \}
Using the sets A and B mentioned above, the resulting difference of A-B is:
A-B = \{ 2, 4, 6, 12 \}
Set complement
The complement of a set A, is the set formed by the elements that belong to the universe U and do not belong to the set A.
The notation for this operation is ^{\text{C}} and is defined as:
A^{\text{C}} = \{ x / x \in U \ \text{ and } \ x \notin A\}
Using the above sets of A and B we have the following:
A = \{ 1, 2, 3, 4, 6, 12 \}
B = \{ 1, 3, 5, 15\}
U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 \}
The complements of both the A set and the B set are as follows:
A^{\text{C}} = \{ 5, 7, 8, 9, 10, 11, 13, 14, 15, 16\}
B^{\text{C}} = \{ 2, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16\}
Set properties
| Identity property | A\cup \varnothing = A A \cup U = U A \cap U = A A \cap \varnothing = \varnothing |
| Idempotency property | A \cup A = A A \cap A = A |
| Complement property | A \cup A^{\text{C}} = U A \cap A^{\text{C}} = \varnothing |
| Associative property | (A \cup B)\cup C = A \cup (B \cup C) (A \cap B) \cap C = A \cap (B \cap C) |
| Commutative property | A \cup B = B \cup A A \cap B = B \cap A |
| Distributive property | A \cup (B \cap C) = (A \cup B) \cap (A \cup C) A \cap (B \cup C) = (A \cap B) \cup (A \cap C) |
Thank you for being in this moment with us : )
