Next we will see one of the most present distributions in probability, which is the hypergeometric distribution, which we will explain below.
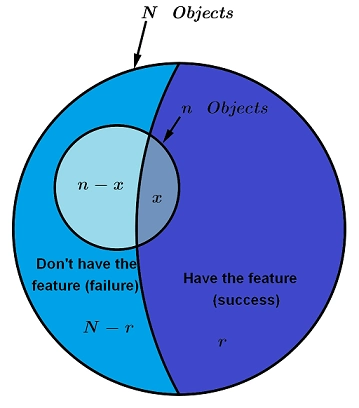
This distribution consists of extracting a random sample of size n without replacement or consideration of its order, from a set of N objects.
That is to say that the events are dependent and of the N objects, r has the feature that interests us, in addition, the random variable X is the number of objects in the sample that have that feature.
So to make this clearer, there are combinations N \choose n equally likely ways to select n objects, thus giving to achieve x successes, x objects must be selected from among the r that have the feature we are interested in, having r \choose x ways and also the n - x objects of the N - r objects that do not have the feature, having combinations {N-r} \choose{n-x}.
Hypergeometric distribution formulas
Using the classic probability formula and the multiplication rule, the probability density is obtained as follows:
P[X = x] = \cfrac{ {r\choose x} {N-r \choose n-x} }{N \choose n }\quad \text{max}[0,n-\left(N-r\right) \le x \le \ \text{min}\left(n,r\right)]
Its most important characteristics are those shown below the expectation and variance
E[X] = n \left( \cfrac{r}{N} \right)
Var[X] = n \left( \cfrac{r}{N} \right) \left( \cfrac{N - r}{N} \right) \left( \cfrac{N-n}{N-1} \right)
The meaning of the unknowns in the above formulas are as follows:
- N is our batch population
- r which are our defective units per batch
- n which is the number of units being tested
- x is expected, to calculate the probability that x quantities have some condition
Hypergeometric distribution example
A foundry ships blocks in batches of 20 units. No manufacturing process is perfect, so bad blocks are inevitable. However, it is necessary to destroy them to identify the defect. Three units are selected and tested before a lot is accepted. Suppose a given lot includes five defective units.
a) Express the density function.
For this exercise we have our following data:
- N = 20 units
- r = 5 defective units
- n = 3 units that are tested
With these data we can proceed to write our density formula:
P[X = x] = f(x) = \cfrac{ {r\choose x} {N-r \choose n-x} }{N \choose n } = \cfrac{ {5\choose x} {20-5 \choose 3-x} }{20 \choose 3 } \quad x = 0,1,2,3
So now we have to calculate each of the probabilities with the values of x, which is the probability that none, one, two or three are defective:
x= 0 \qquad f(x) = \cfrac{ {5\choose 0} {15 \choose 3-0} }{20 \choose 3 } = \cfrac{91}{228}\approx 0.399
There is a 39.9% chance that zero units will be defective.
x= 1 \qquad f(x) = \cfrac{ {5\choose 1} {15 \choose 3-1} }{20 \choose 3 } = \cfrac{35}{76}\approx 0.46
There is a 46% chance that one unit will be defective.
x= 2 \qquad f(x) = \cfrac{ {5\choose 2} {15 \choose 3-2} }{20 \choose 3 } = \cfrac{5}{38}\approx 0.131
There is a 13.1% chance that two units will be defective.
x= 3 \qquad f(x) = \cfrac{ {5\choose 3} {15 \choose 3-3} }{20 \choose 3 } = \cfrac{1}{114}\approx 0.008
There is a 0.8% chance that three units will be defective.
b) Find the expected value of defective units.
To find this value we will apply the expectation formula:
E(X) = n\left( \cfrac{r}{N}\right) = 3\left(\cfrac{5}{20} \right) = \cfrac{3}{4} = 0.75
So our expectation of getting defective units is 0.75 or 75%
c) Find the variance for this case.
And to find the value of the variance we will also apply the pure formula:
Var(X)=n\left(\cfrac{r}{N}\right)\left(\cfrac{N-r}{N}\right)\left(\cfrac{N-n}{N-1}\right)
=3\left(\cfrac{5}{20}\right)\left(\cfrac{20-5}{20}\right)\left(\cfrac{20-3}{20-1}\right)
3\left(\cfrac{5}{20}\right)\left(\cfrac{15}{20}\right)\left(\cfrac{17}{19}\right) = \cfrac{153}{304}
Which gives us an approximate value of the variance of 0.5032
That’s all, we hope that the hypergeometric distribution has been understood as well as possible.
Thank you for being in this moment with us : )
