▷ Correlation Analysis | Explanation and Example

In the regression analysis we connect an independent variable with a dependent variable, but when both variables are random, a correlation analysis must be performed.

In the correlation analysis we do not want to find a linear relationship between two variables, we try to measure the intensity of the linear relationship between $X$ and $Y$ .

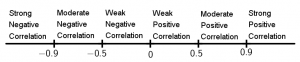
Values of the correlation coefficient

This parameter of the correlation coefficient assumes values between $-1$ and $1$ :

If $r = 1$ , the correlation is perfect positive.
If $r = -1$ , the correlation is perfect negative.
If $r = 0$ , there is no correlation between both variables.

It can be interpreted as follows:

Formula to calculate the correlation coefficient

There are a lot of calculations to arrive at the formula of the correlation coefficient, but we are going to save all those calculations and go straight with the formula:

$r = \cfrac{n\sum xy - \sum x \sum y}{\sqrt{\left[ n\sum x^{2} - (\sum x)^{2}\right] \left[n \sum y^{2} - ( \sum y)^{2} \right]}}$

Great, now that we have the formula, let’s go with the exercise!

Exercise of the correlation coefficient

In a study of ground movement caused by earthquakes, the maximum speed (in m/s) and the maximum acceleration (in m/s $^{2}$ ) were recorded for five of them. The results are presented in the following table:

\begin{array}{| c | c |} \hline \text{Speed} & \text{Acceleration} \\ \hline 1\text{.}54 & 7\text{.}64 \\ 1\text{.}60 & 8\text{.}04 \\ 0\text{.}95 & 8\text{.}04 \\ 1\text{.}30 & 6\text{.}37 \\ 2\text{.}92 & 5\text{.}00 \\ \hline \end{array}

Calculate the correlation coefficient
Someone suggests modifying the units to centimeters and minutes. What effect would it have on the correlation?

Section 1. Calculate the correlation coefficient

Excellent, let’s first calculate the correlation coefficient, for that we need: $\sum x$ , $\sum y$ , $\sum xy$ , $\sum x^{2}$ and $\sum y^{2}$ . First, let’s calculate $\sum x$ and $\sum y$ :

\begin{array}{| c | c |} \hline \text{Speed} & \text{Acceleration} \\ \hline 1\text{.}54 & 7\text{.}64 \\ 1\text{.}60 & 8\text{.}04 \\ 0\text{.}95 & 8\text{.}04 \\ 1\text{.}30 & 6\text{.}37 \\ 2\text{.}92 & 5\text{.}00 \\ \hline \sum x = 8\text{.}31 & \sum y = 35\text{.}09 \\ \hline \end{array}

Let’s calculate $\sum xy$ :

\begin{array}{| c | c | c |} \hline \text{Speed} & \text{Acceleration} & xy \\ \hline 1\text{.}54 & 7\text{.}64 & 11\text{.}7656 \\ 1\text{.}60 & 8\text{.}04 & 12\text{.}864 \\ 0\text{.}95 & 8\text{.}04 & 7\text{.}638 \\ 1\text{.}30 & 6\text{.}37 & 8\text{.}281 \\ 2\text{.}92 & 5\text{.}00 & 14\text{.}6 \\ \hline & & \sum xy = 55\text{.}1486 \\ \hline \end{array}

Now let’s calculate $x^{2}$ :

\begin{array}{| c | c | c |} \hline \text{Speed} & \text{Acceleration} & x^{2} \\ \hline 1\text{.}54 & 7\text{.}64 & 2\text{.}3716 \\ 1\text{.}60 & 8\text{.}04 & 2\text{.}56 \\ 0\text{.}95 & 8\text{.}04 & 0\text{.}9025 \\ 1\text{.}30 & 6\text{.}37 & 1\text{.}69 \\ 2\text{.}92 & 5\text{.}00 & 8\text{.}5264 \\ \hline & & \sum x^{2} = 16\text{.}0505 \\ \hline \end{array}

Now let’s calculate $y^{2}$ :

\begin{array}{| c | c | c |} \hline \text{Speed} & \text{Acceleration} & y^{2} \\ \hline 1\text{.}54 & 7\text{.}64 & 58\text{.}3696 \\ 1\text{.}60 & 8\text{.}04 & 64\text{.}6416 \\ 0\text{.}95 & 8\text{.}04 & 64\text{.}6416 \\ 1\text{.}30 & 6\text{.}37 & 40\text{.}5769 \\ 2\text{.}92 & 5\text{.}00 & 25\text{.}00 \\ \hline & & \sum y^{2} = 253\text{.}2297 \\ \hline \end{array}

Now let’s directly replace the values in the formula:

$r = \cfrac{(5)(55\text{.}1486) - (8\text{.}31)(35\text{.}09)}{\sqrt{\left[(5)(16\text{.}0505) - (8\text{.}31)^{2} \right] \left[(5)(253\text{.}2297) - (35\text{.}09)^{2} \right]}}$

$r = -0\text{.}8027$

The correlation coefficient is $r=-0\text{.}8027$ , so it indicated that it is a moderate negative correlation.

Section 2. Someone suggests modifying the units to centimeters and minutes

The truth is that it would have no effect if we change the values to centimeters and minutes since it would only be a change of units, that is, the correlation would be the same, but we are going to check it anyway. First, let’s calculate $\sum x$ and $\sum y$ :

\begin{array}{| c | c |} \hline \text{Speed (cm/min)} & \text{Acceleration (cm/min}^{2}\text{)} \\ \hline 9240 & 45840 \\ 9600 & 45840 \\ 5700 & 48240 \\ 7800 & 38220 \\ 17520 & 30000 \\ \hline \sum x = 49860 & \sum y = 210540 \\ \hline \end{array}

Now let’s calculate the sum of $x$ by $y$ :

\begin{array}{| c | c | c |} \hline \text{Speed} & \text{Acceleration} & xy \\ \hline 9240 & 45840 & 423561600 \\ 9600 & 45840 & 463104000 \\ 5700 & 48240 & 274968000 \\ 7800 & 38220 & 298116000 \\ 17520 & 30000 & 525600000 \\ \hline & & \sum xy = 1985349600 \\ \hline \end{array}

Now let’s calculate $x^{2}$ :

\begin{array}{| c | c | c |} \hline \text{Speed} & \text{Acceleration} & x^{2} \\ \hline 9240 & 45840 & 85377600 \\ 9600 & 45840 & 92160000 \\ 5700 & 48240 & 32490000 \\ 7800 & 38220 & 60840000 \\ 17520 & 30000 & 306950400 \\ \hline & & \sum x^{2} = 577818000 \\ \hline \end{array}

Now let’s calculate $y^{2}$ :

\begin{array}{| c | c | c |} \hline \text{Speed} & \text{Acceleration} & y^{2} \\ \hline 9240 & 45840 & 2101305600 \\ 9600 & 45840 & 2327097600 \\ 5700 & 48240 & 2327097600 \\ 7800 & 38220 & 1460768400 \\ 17520 & 30000 & 900000000 \\ \hline & & \sum y^{2} = 9116269200 \\ \hline \end{array}

Now what we are going to do is put all those calculated values in the formula to find the correlation coefficient:

$r = \cfrac{(5)(1985349600) - (49860)(21054)}{\sqrt{\left[ (5)(577818000) - (49860)^{2}\right] \left[(5)(9116269200) - (210540)^{2} \right]}}$

Using a calculator, we will obtain the following value:

$r = -0\text{.}8027$

So you can verify that the correlation coefficients do not change even if they have different units, it also means that it is still a moderate negative correlation!

Thank you for being at this momento with us : )