Among so many probability theorems, here we present one that many of us have heard, the well-known Bayes Theorem. That is why we have brought you an explanation and an example to illustrate the Bayes Theorem.
Let’s go with the explanation of the Bayes Theorem
We have several events that are A_{1},A_{2},A_{3},..,A_{k},..,A_{n}, that form a partition with S, and E is any event. Now we apply the previously seen in the conditional probability formula:
P(A_{k}|E) = \cfrac{P(A_{k}\cap E)}{P(E)} = \cfrac{P(A_{k})P(E|A_{k})}{P(E)}
The part P(A_{k}|E) of the previous formula reads:
The probability that it was A_{k} given that E already happened.
Formula of Bayes Theorem
If we consider the previous formula obtained to calculate the total probability of E, we must apply the sum shown below to calculate the total probability of E because there are several cases in the exercises that require the use of this formula, what is shown below is the Formula of Bayes Theorem:
\displaystyle P(A_{k}|E) = \cfrac{P(A_{k})P(E|A_{k})}{\sum_{i=1}^{n}P(A_{i})P(E|A_{i})}
The sum of the denominator reads like this:
The sum of the probability of A_{i} multiplied by the probability that it is E given that A_{i} already occurred.
Example of Bayes Theorem
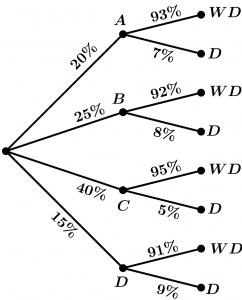
The company X uses four transportation companies: A_{1}, A_{2}, A_{3} and A_{4}. It is known that 20% of the shipments are assigned to the company A_{1}, 25% to the A_{2}, 40% to the A_{3} and 15% to the A_{4}. Shipments are delayed to their customers by 7% if they are delivered by A_{1}, 8% if they are derivered by A_{2}, 5 if A_{3} and 9% if A_{4}. If we know that today’s shipment was delivered late, what is the probability that the company A_{1} was in charge of doing it?
Many of you will already know how to solve this exercise quickly, but let’s explain it step by step. We will represent the information in the following table:
\begin{array}{| c | c |}
\hline
\text{Shipments} & \text{Delivery} \\
\hline
A_{1} = 20 \% & \text{Delay (D)} = 7\% \\
A_{2} = 25\% & \text{Delay (D)} = 8\% \\
A_{3} = 40\% & \text{Delay (D)} = 5\% \\
A_{4} = 15\% & \text{Delay (D)} = 9\% \\
\hline
\end{array}WD= Without delay, D= Delayed
The logistics team is informing us from the booth that an order arrived and was delayed, and what we want to know is if the company was A_{1}, in other words, to know if it was A_{1} to which it was already delayed, then we will use the formula of the Bayes Theorem:
\displaystyle P(A_{1}|R) = \cfrac{P(A_{1})P(R|A_{1})}{\sum_{i=1}^{4}P(A_{i})P(R|A_{i})}
n is equal to 4 because we are going to represent the probability of the delay of the 4 companies. Let’s find it:
\displaystyle \sum_{i=1}^{4}P(A_{i})P(R|A_{i}) = P(A_{1})P(R|A_{1}) + P(A_{2})P(R|A_{2}) + P(A_{3})P(R|A_{3}) + P(A_{4})P(R|A_{4})
With the written table, it is easier to place the values, see the summation with the values in the table:
\displaystyle \sum_{i=1}^{4}P(A_{i})P(R|A_{i}) = (20\%)(7\%) + (25\%)(8\%) + (40\%)(5\%) + (15\%)(9\%)
You can grab a calculator to speed up the process of multiplying and adding:
\displaystyle P = (E) = \sum_{i=1}^{4}P(A_{i})P(R|A_{i}) = \cfrac{7}{500} + \cfrac{1}{50} + \cfrac{1}{50} + \cfrac{27}{2000} = \cfrac{27}{400}
We only need to calculate the probability of the numerator of the Bayes Theorem formula, which has P(A_{1}) which is 20\% and has P\left(\frac{E}{A_{1}}\right) which is the probability that it arrived late if it already happened that it arrived in the shipment A_{1} that has a probability of 7\%. Now, let’s replace all these values in the Bayes Theorem formula:
P(A_{1}|E) = \cfrac{\cfrac{20}{100} \cdot \cfrac{7}{100}}{\cfrac{27}{400}} = \cfrac{28}{135}=0.2074
So the probability of a boat arriving late and also coming from the boat A is 0.2074 which is equal to 20.74\%
Thank you for being at this moment with us : )