How to know if two triangles are similar
“Two triangles are similar if the homologous angles are congruent and the homologous sides are proportional.” (Colonia, 2004, p.289)
Note: the “\Rightarrow” that will be shown below means “then:”.
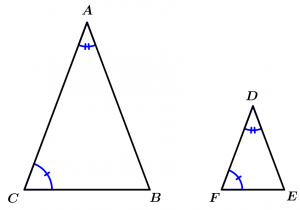
Postulate of the similarity AAA (Angle-Angle-Angle)
If the 3 angles of a triangle are congruent with the 3 angles of another triangle, then the triangles are similar.
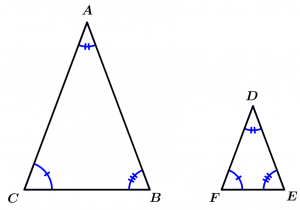\text{If } \ \measuredangle A \cong \measuredangle D, \measuredangle B \cong \measuredangle E \ \land \ \measuredangle C \cong \measuredangle F
\Rightarrow \Delta ABC \sim \Delta DEF
Theorems relating to similarities of triangles
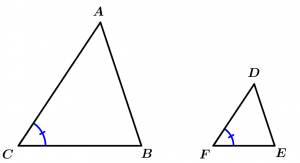
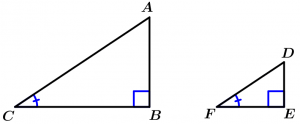
Theorem 1. Similarity AA (Angle-Angle)
If two angles of a triangle are congruent with two angles of another triangle, then the triangles are similar.
\text{If } \measuredangle A \cong \measuredangle D \ \land \ \measuredangle C \cong \measuredangle F
\Rightarrow \Delta ABC \ \sim \ \Delta DEF
Theorem 2. Similarity SSS (Side-Side-Side)
If two triangles have their 3 sides proportional, then the triangles are similar.
\text{If } \ \cfrac{\overline{AB}}{\overline{DE}} = \cfrac{\overline{BC}}{\overline{EF}} = \cfrac{\overline{CA}}{\overline{FD}}
\Rightarrow \Delta ABC \ \sim \ \Delta DEF
Theorem 3. Similarity SAS (Side-Angle-Side)
If two triangles have two proportional sides and the angles between these sides are congruent, the triangles are similar.
\text{If } \ \cfrac{\overline{CA}}{\overline{FD}} = \cfrac{\overline{CB}}{\overline{FE}} \ \land \ \measuredangle C \cong \measuredangle F
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
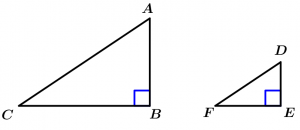
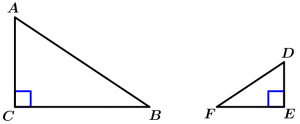
Theorem 4
If two right triangles have their proportional legs, the triangles are similar.
\text{If } \measuredangle B \ \land \measuredangle E \ \text{ are right angles} \ \land
\cfrac{\overline{BA}}{\overline{ED}} = \cfrac{\overline{BC}}{\overline{EF}}
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
Theorem 5
If two right triangles have a congruent acute angle, the triangles are similar
\text{If } \ \measuredangle B \ \land \ \measuredangle E \ \text{are right angles } \land
\measuredangle C \cong \measuredangle F
\Rightarrow \Delta ABC \ \sim \ \Delta DEF
Theorem 6
If two right triangles have the hypotenuse and a proportional leg, then the triangles are similar.
\text{If } \measuredangle C \ \land \measuredangle \ E \text{ are right angles } \ \land
\cfrac{\overline{AB}}{\overline{DF}} = \cfrac{\overline{AC}}{\overline{DE}}
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
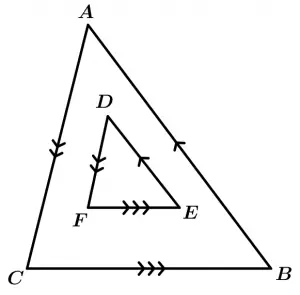
Theorem 7
If two triangles have their corresponding sides parallel to each other, they are similar.
\text{If } \overline{BA} \parallel \overline{ED}, \ \overline{AC} \parallel \overline{DF}, \ \overline{CB} \parallel \overline{FE}
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
It does not necessarily have to be one triangle inside another to identify that they have their parallel sides, they can be outside each other as shown below:
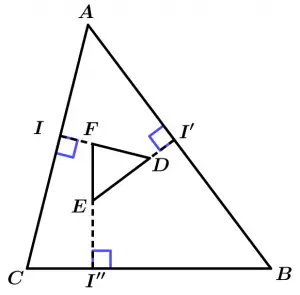
Theorem 8
If each side of a triangle is perpendicular to a corresponding side of the second triangle, then they are similar triangles.
\text{If } \ \overline{DI} \bot \overline{AC}, \overline{EI'} \bot \overline{AB} \ \land \ \overline{FI''} \bot \overline{CB}
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
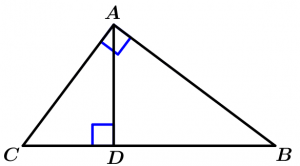
Theorem 9
The corresponding height divides the right triangle given in two similar to it and similar to each other. It means that we have 3 similar triangles. Further, the length of the height corresponding to the hypotenuse is the proportional mean between the lengths of the two segments that divide the hypotenuse.
\text{If } \Delta ABC \ \text{ is rectangle being:}
\overline{CB} \ \text{ the hypotenuse } \ \land \ \overline{DA}
\text{the height}
\Rightarrow \ \Delta ABC \ \sim \ \Delta ADC \ \sim \ \Delta ADB
\land \ \text{ the proportional mean is}
\Rightarrow \ \cfrac{\overline{CD}}{\overline{AD}} = \cfrac{\overline{AD}}{\overline{DB}}
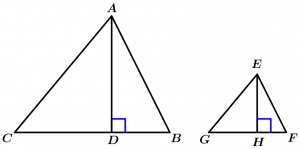
Properties of the heights of similar triangles
Theorem 10
The corresponding heights of two similar triangles are proportional to the homologous sides.
\text{If } \Delta ABC \ \sim \ \Delta EFG \ \land
\overline{AD} \ \land \ \overline{EH} \ \text{ they are corresponding heights}
\text{to the sides homologous } \ \overline{CB} \ \land \ \overline{GF}
\Rightarrow \ \cfrac{AD}{EH} = \cfrac{CB}{GF}
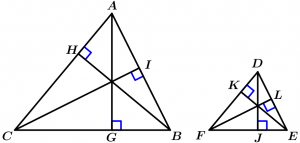
Theorem 11
The corresponding heights of two similar triangles are proportional.
\text{If } \Delta ABC \ \sim \ \Delta DEF \ \land
\overline{AG}, \overline{CI}, \overline{BH}, \overline{DJ}, \overline{FL} \ \land \ \overline{EK} \text{ are heights}
\Rightarrow \cfrac{\overline{AG}}{\overline{DJ}} = \cfrac{\overline{CI}}{\overline{FL}} = \cfrac{\overline{BH}}{\overline{EK}}
Thank you for being at this moment with us :)
