Triangle area
For the calculation of the area of the triangle, we will use the famous base formula for height over two:
A = \cfrac{b\cdot h}{2}
And we are going to see 3 ways in which triangles can be presented to us when applying the aforementioned formula because sometimes the brain deceives us.
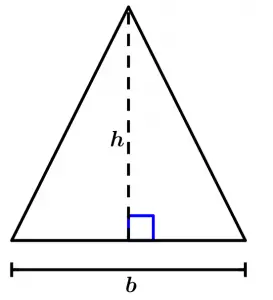
First form
This first form is when the triangle can be drawn a height that is above the base and not at the corners of the base or outside the base.
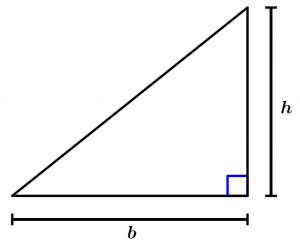
Second form
The second form is when you are presented with a right triangle, whose height is its own vertical leg.
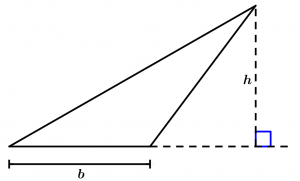
Third form
The third form is when we present a triangle to which we do not know how to draw a height, to do that we will imaginary extend the length of the base (but the base will be the same) until it forms a line perpendicular to the highest point, and once we have the height we only apply the aforementioned formula.
Heron’s formula
We can not miss the formula of Heron, where we have a semiperimeter that will help us write the formula, the semiperimeter Sp is simply the perimeter of the triangle divided by 2:
Sp = \cfrac{a + b + c}{2}
And Heron’s formula for calculating the area of a triangle is the following:
A = \sqrt{Sp\left(Sp - a \right) \left(Sp - b \right) \left(Sp - c\right)}
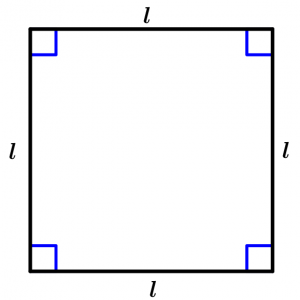
Square area
The area of the square is equal to the square of any of its sides (l):
A = l^{2}
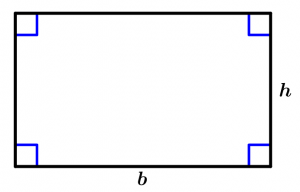
Rectangle area
The area of a rectangle is equal to the product of the base (b) by height (h):
A = b\cdot h
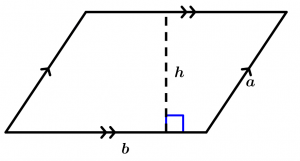
Parallelogram area
A parallelogram with sides a, b and height h have an area equal to the product of one of its sides by the corresponding height on that side.
In the following parallelogram we observe that the area is the side b (which acts as base) multiplied by the height (h) of that side:
A = b\cdot h
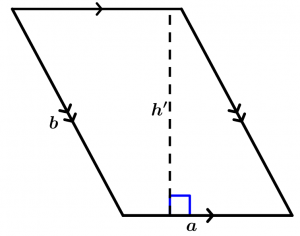
The next figure that we will observe is the same parallelogram only that rotated, we will see how it is that the height changes because now the base is the side a:
A = a\cdot h'
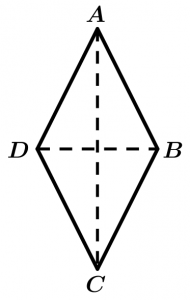
Rhombus area
The area of the diamond is equal to half the product of its diagonals:
A = \cfrac{\left( AC\right) \left(DB \right)}{2}
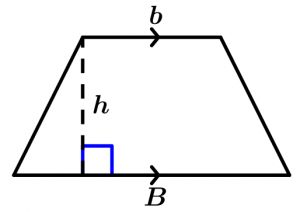
Trapeze area
The area of the trapezium is equal to the semisum of its parallel sides multiplied by its height:
A = \left(\cfrac{B + b }{2}\right)h
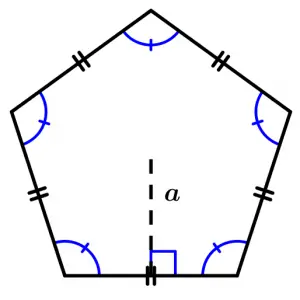
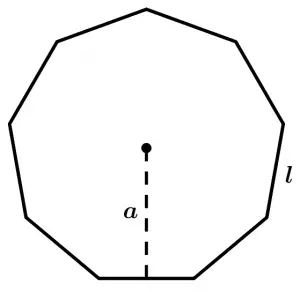
Regular polygons area
The area of a regular polygon is its perimeter (P) multiplied by the apothem (a) divided by two:
A = \cfrac{P\cdot a}{2}
When we talk about regular polygons, we are talking about hexagons, heptagons, octagons, regular n-gons.
Example of calculating the area of a regular nonagon
The following regular nonagon has an apothem a of 2.06 cm and its side l measures 1.5 cm, calculates its area:
The perimeter of the nonagon is calculated by multiplying the length of the side l by its number of sides, which in this case is 9:
P = l\cdot 9 = 1.5 \cdot 9 = 13.5 \ cm
Now we apply the formula of the area:
A = \cfrac{P\cdot a}{2} = \cfrac{13.5 \ cm \ \cdot 2.06 \ cm}{2} = 13.905\ cm^{2}
So the area of our nonagon is 13.905 \ cm^{2}
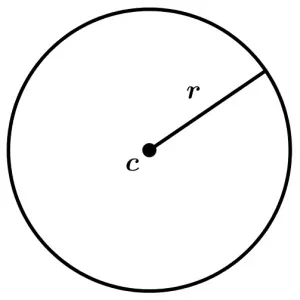
Circle area
The area of a circle is equal to \pi per radius (r) squared:
A = \pi\cdot r^{2}
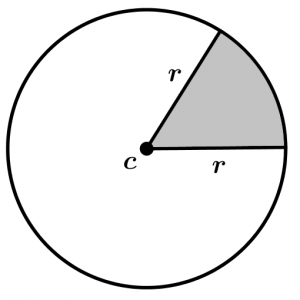
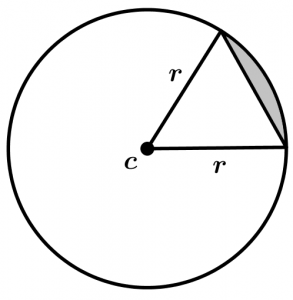
With what you learned and a little common sense you can now calculate the area of a circular sector and the area of a circular segment. The shaded areas represent the circular sector and the circular segment respectively:
You will see that calculating those areas is easier than it seems, luck ; )
Thank you for being at this moment with us :)