Have we ever heard the word “parabola”, and yes, it is a beautiful curve which is used a lot in everyday life as in some lenses, in parabolic antennas, in some tunnels and sometimes to complicate a bit the existence in school . So let’s first look at the elements of the parabolas and then look at the types of parabolas in math.
Elements of a parabola
The parts of a parabola that we will mention are the following:
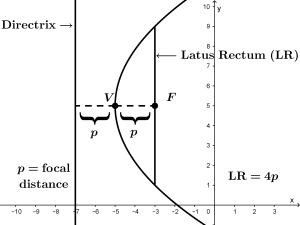
Vertex of the parabola
The vertex of the parabola is the point from which it opens the parabola, and it also indicates where the parabola is located. It is usually represented with the point V of vertex.
Focus of the parabola
Take the case of a satellite dish, in the practical case the focus is very important because all the signals that reach the parabola will be received in the focus, no matter the point that the signal touches the satellite dish, it will always reach the focus. It is usually represented as the F focus point.
Focal length of the parabola
The focal length is the length between the vertex and the focus.
Straight side of the parabola
The straight side is a line perpendicular to the line that joins the vertex and the focus and that has four times the length of the focal distance.
Let’s summarize all the parts of the parabola mentioned in the following graph
Types of parabolas
We will classify the parabolas with respect to whether they are horizontal, vertical and if they open to the right or to the left, we will place their graphic representation of the parabolas and their respective equations.
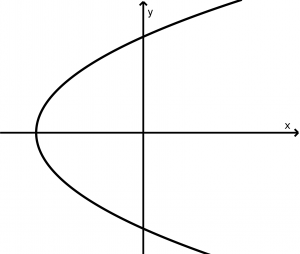
Horizontal parabola that opens to the right
(y-y_{0})^{2} = 4p(x - x_{0})
x-(x_{0} - p) = 0
F(x_{0} + p, y_{0})
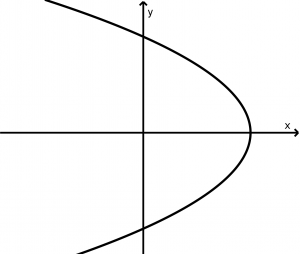
Horizontal parabola that opens to the left
(y-y_{0})^{2} = -4p(x-x_{0})
x - (x_{0}+p) = 0
F(x_{0} \ -p, y_{0})
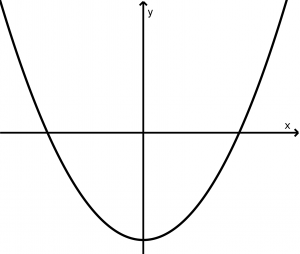
Vertical parabola that opens upwards
(x-x_{0})^{2} = 4p(y - y_{0})
y - (y_{0} - p ) = 0
F(x_{0}, y_{0} + p)
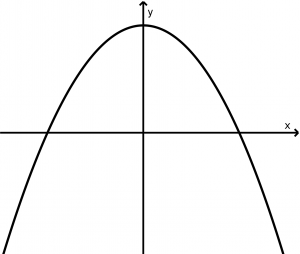
Vertical parabola that opens down
(x - x_{0})^{2} = -4p(y - y_{0})
y-(y_{0} + p )= 0
F(x_{0}, y_{0} - p)
Thank you for being at this moment with us : )