Mediatrix

The definition of a mediatrix

It is called a mediatrix to the perpendicular line drawn on one side at the midpoint. If all the mediatrices of a polygon cut at the same point, it is known as a circumcenter. All triangles have a circumcenter and not all polygons such as quadrilaterals, pentagons, etc. have circumcenter.

Let’s go with the examples of the mediatrixes

For these examples of mediatrices we will work with triangles because they are simple, they only have 3 sides and interesting things can be done with them. Our triangles are the following:

\overline{DE} = \overline{EF} = \overline{FD}

\measuredangle GHI = 90^{\text{o}}

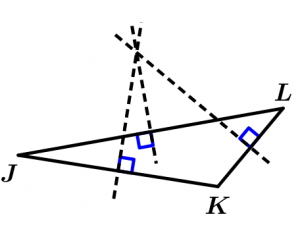
\overline{JK} \neq \overline{KL} \neq \overline{LJ}

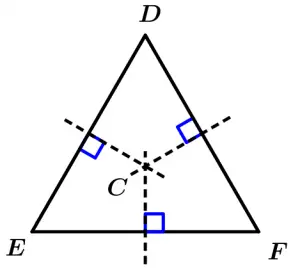
Now at the midpoint of each side of each triangle we will draw a segment perpendicular to each side, let’s first see the mediatrices of the equilateral triangle:

Now the mediatrix of each side of the right triangle:

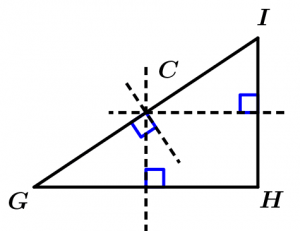
Now we go with the scalene triangle:

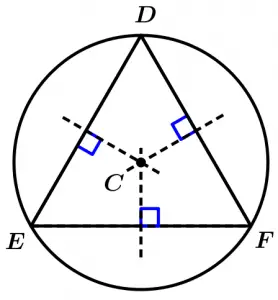
Now we are going to observe something very interesting: the point where the mediatrices intersect is known as circumcenter, which is the center of a circle that passes through the vertices of the triangle, which means that the distance from each vertex of the triangle to the circumcenter is equal to the radius of the circumference, so from any vertex of the triangle to the circumcenter we will have the same distance, in addition it can be observed that we will have an inscribed triangle. Let’s see some examples with the previous triangle, let’s draw the circumference of our equilateral triangle:

Let’s draw the circumference of the right triangle:

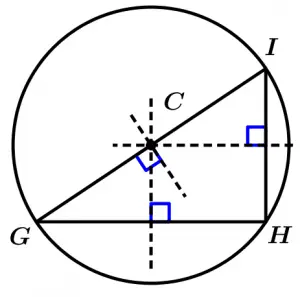
Finally, draw the circumference of the scalene triangle:

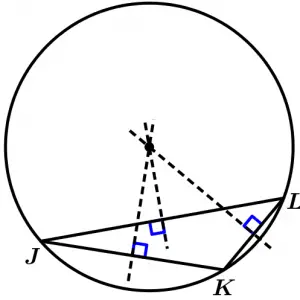
Do not you find it surprising? With this we saw some applications that have the mediatrices that help to determine the circumcenters of regular polygons such as cubes, pentagons, hexagons, etc., but there are still many irregular polygons that do have circumcenter and therefore are inscribed. If we try to find the mediatrix of some irregular polygon we will realize that an intersection of all the mediatrices does not occur, so there is no circumcenter. For example, let’s look at the following irregular polygon:

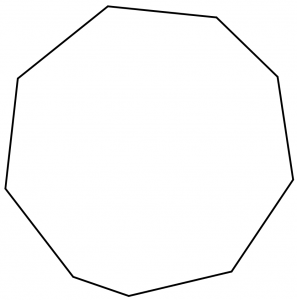
Let’s draw the mediatrices of the nonagon:

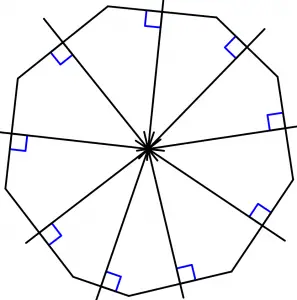
Now what we will see is a circumference that passes through each of the vertices of the nonagon:

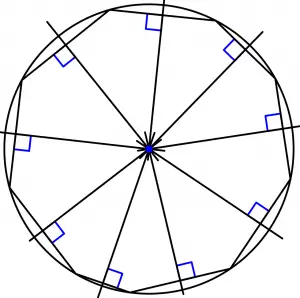
So we saw that you do not need a regular polygon to have circumcenter, our nonagon has circumcenter and is an irregular polygon, finally remember that not all irregular polygons have circumcenter.

Thank you for being at this moment with us :)