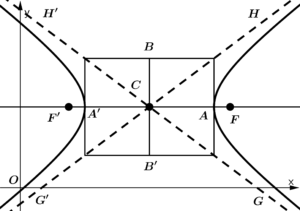
In a hyperbola, A and A' will always be used to represent the vertices, and B and B' are used to represent the ends of the segment perpendicular to the segment \overline{AA'}. First of all, I want to clarify that with a little practice it will already be possible to discern when a is less than or greater than b and know if the hyperbola opens up and down or to the right and left.
Parts of the hyperbola with center at C(x_{0}, y_{0}) and segment \overline{AA'} parallel to the x axis
Let’s see our base figure of the hyperbola with which we will define the formulas and the elements of the hyperbola:
Equations of the hyperbola in rectangular coordinates:
The equation of the hyperbola that opens to the right and left has the peculiarity that the sign of the fraction that contains the y‘s will be negative:
\cfrac{(x - x_{0})^{2}}{a^{2}} - \cfrac{(y - y_{0})^{2}}{b^{2}} = 1
The coordinates x_{0} and y_{0} always represent the center C for any hyperbola, no matter if it is a hyperbola that opens to the right and left or a hyperbola that opens up and down.
- c represents the length of the segment \overline{CF} where \overline{CF} =\overline{CF'}.
- a represents the length of the segment \overline{CA} where \overline{CA}=\overline{CA'}.
- b represents the length of the segment \overline{CB} where \overline{CB}=\overline{CB'}.
Segment length \overline{AA'}
The length of the segment \overline{AA'} is 2a.
Segment length \overline{BB'}
The length of the segment \overline{BB'} is 2b.
Length from center to foci (c)
The distance from the center C to the foci F or F' is:
c = \sqrt{a^{2} \ + b^{2}}
Eccentricity of the hyperbola
The formula to calculate the eccentricity of the hyperbola is the next:
\epsilon = \cfrac{c}{a}
The eccentricity can only take values greater than 1: \epsilon>1, but now:
What does the eccentricity in the hyperbola mean or what does it represent?
It means that if the value of the eccentricity is closer to 1, the hyperbola tends to be a line with a segment removed (this happens because the hyperbola looks so closed that it looks like a line), and the larger the value of the eccentricity, the hyperbola tends to resemble a pair of parallel lines.
Slopes of the asymptotes of the hyperbola
The slopes of the asymptotes of the hyperbola \overline{G'H} and \overline{GH'} are calculated by dividing the value of the vertical segment by the horizontal segment:
= \pm \cfrac{\text{vertical segment}}{\text{horizontal segment}}
The symbol \pm means that the two signs will be used since the hyperbola has two asymptotes, which means that the slope that we obtain will be positive and negative due to its two asymptotes, in a moment we will see it with an example.
Point of the hyperbola towards the foci
If P is any point on the hyperbola, PF \ - PF' = \pm 2a. The \pm symbol depends on the branch.
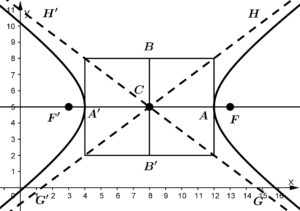
Example of hyperbola with center at the origin C(x_{0}, y_{0}) and with segment \overline{AA'} parallel to the axis x
The equation of the hyperbola is:
\cfrac{(x - 8)^{2}}{4^{2}} - \cfrac{(y - 5)^{2}}{3^{3}} = 1
The center of hyperbola
As can be seen, the center C of the hyperbola is at:
C(8,5)
That means that the center of our hyperbola will be found in the values that x_{0} and y_{0} have, only that we will place the opposite signs in our coordinate, that means that as our value of x_{0} is -8 and our value of y_{0} is -5, then our coordinate of the center of the hyperbola will be C(8,5).
Length of segment \overline{AA'}
The length of the segment \overline{AA'} is equal to 8, which means that the length of a is equal to 4.
Length of segment \overline{BB'}
The length of the segment \overline{BB'} is equal to 6, which means that the length of b is equal to 3.
Distance from center to foci
The distance from the center C to either of the foci, either F or F' is:
c = \sqrt{4^{2} + 3^{2}} = \sqrt{16 + 9} = \sqrt{25} = 5
So the focus F is at the point F(13,5) and the focus F' is at the point F' (3,5).
Eccentricity of the hyperbola
\epsilon = \cfrac{c}{a} = \cfrac{5}{4}=1.25
Slopes of the asymptotes of the hyperbola
The calculation of the slopes of the asymptotes is very simple, we will divide the length of the vertical segment by the length of the horizontal segment:
\pm \cfrac{\text{vertical segment}}{\text{horizontal segment}} = \pm \cfrac{3}{4} = \pm 0.75
So the slope of one asymptote is 0.75 and the slope of the other asymptote is -0.75.
Point of the hyperbola towards the foci
You can make this proof quickly by grabbing as P any vertex of the hyperbola and you will easily see that the formula PF \ - PF'= \pm 2a is demonstrated. Try taking the vertex (4,5).
Why is it not practical to call the axes of the hyperbola “major axis” and “minor axis”?
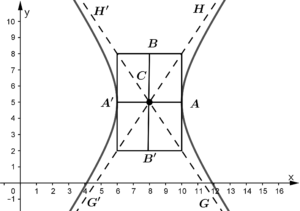
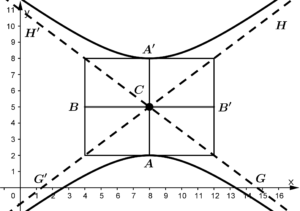
Simply and simply because there would be confusion when using the formulas, look at the following graphs
Graph of hyperbola 1
Graph of hyperbola 2
In the Graph of hyperbola 1 (which is the one in our example) if we mention the major axis we will take the segment \overline{A'A}, and if we mention the minor axis we will take the segment \overline{B'B}, so far we’re doing fine. But what if I told you to take the major axis of the Graph of hyperbola 2? The major axis is now no longer \overline{A'A}, right?
If by studying the formulas you want to determine the slopes of the asymptotic lines of the Graph of hyperbola 2 and you learned the formula as follows:
\pm \cfrac{\text{minor axis}}{\text{major axis}}
You will notice that now the minor axis is horizontal and the major axis is vertical, which means that the slope you obtain will not result in the slope of your asymptotes from your Graph of Hyperbola 2. So to find the slope of the asymptotes of the hyperbola let’s get used to calling the axes “vertical segment” and “horizontal segment”.
\pm \cfrac{\text{vertical segment} }{\text{horizontal segment}}
Hyperbola with center at C(x_{0}, y_{0}) and segment \overline{AA'} parallel to the y axis
Look at the next example:
Which the hyperbola equation is:
\cfrac{(y - 5)^{2}}{3^{2}} - \cfrac{(x - 8)^{2}}{4^{2}} = 1
When the hyperbola opens up and down, the denominator of the fraction that has the y‘s will now be a and the denominator of the fraction that has the x‘s will now be b. Which means that the equation for the hyperbolas that open up and down is:
\cfrac{(y - y_{0})^{2}}{a^{2}} - \cfrac{(x - x_{0})^{2}}{b^{2}} = 1
It is said that the a follows the positive sign and the b follows the negative sign, but all the above formulas are used exactly the same.
Thank you for being in this moment with us : )