The circumference is a locus in which all points are equidistant from a fixed point called the center.
In a mathematical way the circumference is represented by an equation of second degree:
x^{2} + y^{2} = r^{2}
Where the previous equation represents a circle whose center is the origin of the coordinate axis system.
And to represent a circumference with the center outside the origin, we use the following equation:
\left(x - (h) \right)^{2} + \left(y - (k) \right)^{2} = r^{2}
Where h and k represent the center of the circumference at \left( h, k \right).
Let’s analyze two examples of the circumference:
Circumference example 1. Draw the locus represented by the equation x^{2} + y^{2} = 9.
As we can see in the equation of the exercise, it is a circle whose center is the origin and the radius we have to calculate, in this case:
r^{2} = 9
We just have to apply square root to the above equality to get our radius:
r = 3
Finally we can locate our circumference in the Cartesian plane:
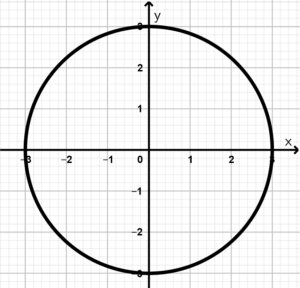
Figure 2. Circumference x^{2} + y^{2} = 9
Let’s see an example where the center isn’t at the origin.
Example of a circumference 2. Draw the locus represented by the equation (x + 1)^{2} + (y - 1)^{2} = 5.
What we can observe in this exercise is that it is not a circumference that is at the origin, if we don’t have much practice, we have to place the appropriate parentheses to the equation of the circumference as shown below:
(x + 1)^{2} + (y - 1)^{2} = (x - (-1))^{2} + (y - (1))^{2} = 5
Perfect, now that we have added the proper parentheses, we can say that the center is at the point:
(-1 , 1)
It would only be necessary to calculate the radius of the circumference, for that we simply have to apply the square root to the 5:
r^{2} = 5 \rightarrow r = \sqrt{5}
And with the center of the circumference and the radius already calculated, we can well proceed to draw our circumference:
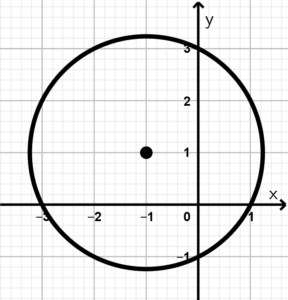
Figure 3. Circumference (x + 1)^{2} + (y - 1)^{2} = 5
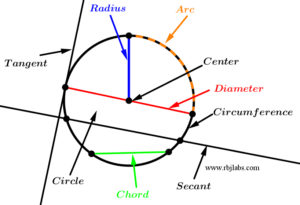
Elements and lines of the circumference
In this section we will mention the parts that make up a circumference and we will also mention the name given to the lines or segments that cut the circumference.
Circumference radius
The radius is a segment that joins the center with any point on the circumference.
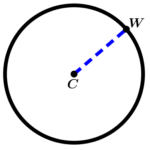
We can see that the radius of the circumference is the segment:
\overline{CW}
Circumference diameter
The diameter is the segment that joins two points on the circumference passing through the center.
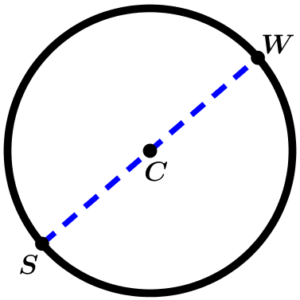
Diameter \overline{WS} passing through the center C.
Arc of circumference
The arc of the circumference is a part of the same circumference delimited by any two points.
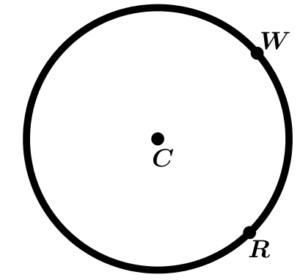
The arc is named as:
\text{Arc } \ \widehat{WR}
String of the circumference
The chord is a segment that joins two points on the circumference.
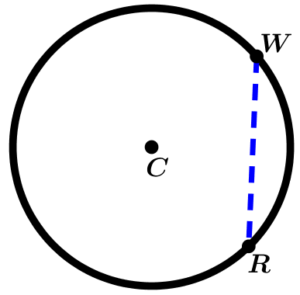
As can be seen in the previous figure, the circumference has a:
\text{String } \ \overline{WR}
Line tangent to the circumference
It is called a tangent line to the circumference when the line touches the circumference at a point, receiving the name of a point of tangency.
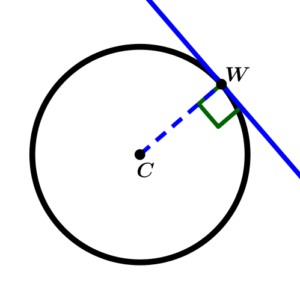
W is the point of tangency.
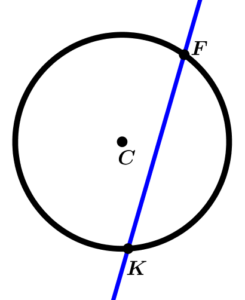
Secant line to circumference
The secant line is the line that crosses the circumference at two points, resulting that a part of the same line is chord of the circumference.
Thank you for being in this moment with us : )
