Triangle classification according to their sides
Equilateral triangle
Equilateral triangles are those that have the same three sides, and because they have the same three sides, they also have the same three angles.
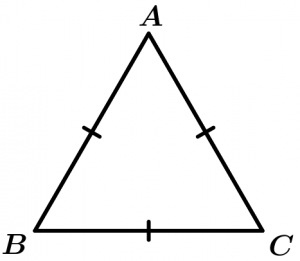
The \Delta ABC is equilateral.
\overline{AB} = \overline{BC} = \overline{AC}
Isosceles triangle
Isosceles triangles are those that have two of their sides equal.
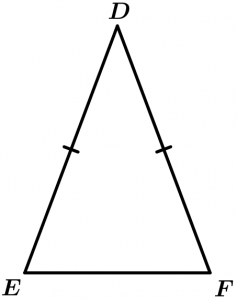
The \Delta DEF is isosceles.
\overline{ED} = \overline{DF}
Because it has two of its sides equal, it has two of its angles equally. The opposite angle of the side DF is equal to the opposite angle of the side DE:
\measuredangle E = \measuredangle F
Scalene triangle
Scale triangles are those that have their three sides unequal.
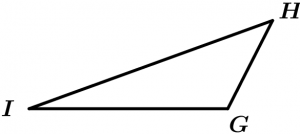
The \Delta GHI is scalene.
\overline{GH} \neq \overline{HI} \neq \overline{IG}
Classification of triangles according to their angles
Right triangle
Right triangles are those that have a right angle. The hypotenuse is the opposite side to the right angle and they are legs on the sides that form the right angle.
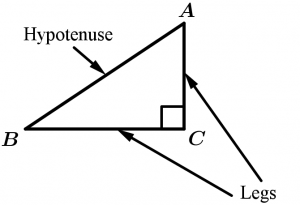
The \Delta ABC is rectangle.
\measuredangle C = 90^{\text{o}}
Acute angle triangle
The acute-angled triangles are those that have acute their three angles.
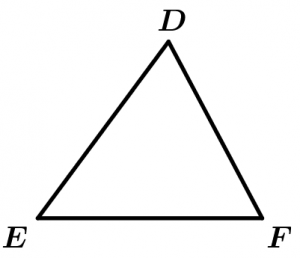
The \Delta DEF is acute-angle.
The \measuredangle D, the \measuredangle E and the \measuredangle F are acute.
Equiangular triangle
It is called equiangular triangle to those that have equal their angles, and yes, it is the equilateral triangle.
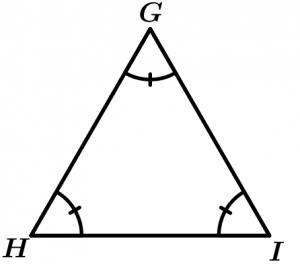
The \Delta GHI is equiangular.
\measuredangle G = \measuredangle H = \measuredangle I
Obtuse triangle
The obtuse triangles are those that have an obtuse angle. The obtuse angle is that angle that measures more than 90 ° and less than 180 °.
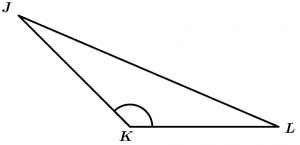
The \Delta JKL is an obtuse triangle.
90^{\text{o}} < \measuredangle K < 180^{\text{o}}
Oblique angle triangle
They are all triangle that are not rectangles. Oblique angle means all that angle that is not right.
Thank you for being at this moment with us:)
