Polygons are classified according to their number of sides, according to their angles and are also classified according to their equality or inequality of their angles and sides, that is, whether they are regular or irregular.
Classification according to the number of sides
Next we will observe a list that contains the first 18 polygons:
\begin{array}{| c | c |}
\hline
\text{Polygons} & \text{Number of sides} \\ \hline \hline \text{Triangle} & 3 \\ \hline \text{Quadrilateral} & 4 \\ \hline \text{Pentagon} & 5 \\ \hline \text{Hexagon} & 6 \\ \hline \text{Heptagon} & 7 \\ \hline \text{Octagon} & 8 \\ \hline \text{Nonagon} & 9 \\ \hline \text{Decagon} & 10 \\ \hline \text{Hendecagon} & 11 \\ \hline \text{Dodecagon} & 12 \\ \hline
\text{Tridecagon} & 13 \\ \hline \text{Tetradecagon} & 14 \\ \hline \text{Pentadecagon} & 15 \\ \hline \text{Hexadecagon} & 16 \\ \hline \text{Heptadecagon} & 17 \\ \hline \text{Octadecagon} & 18 \\ \hline \text{Nonadecagon} & 19 \\ \hline \text{Icosagon} & 20 \\ \hline \end{array}The polygons that have more than 20 sides are known as n-gons, this is done for better comprehension since the polygons of more than 20 sides have not very common names that surely not many have heard, anyway I will mention some of these polygons below so you can see the name that has been assigned to them: you have assigned:
\begin{array}{| c | c |} \hline \text{Polygons} & \text{Number of sides} \\ \hline \hline \text{Icosakaihenagon} & 21 \\ \hline \text{Icosakaidigon} & 22 \\ \hline \text{Icosakaitrigon} & 23 \\ \hline \text{Icosakaitetragon} & 24 \\ \hline \text{Icosakaipentagon} & 25 \\ \hline \text{Icosakaihexagon} & 26 \\ \hline \text{Icosakaiheptagon} & 27 \\ \hline \text{Icosakaioctagon} & 28 \\ \hline \text{Icosakaieneagon} & 29 \\ \hline \end{array}Yes, I understand, the best thing is to say: “polygon of n sides” when the polygon has more than 20 sides.
Classification according to their angles
Depending on the angle formed by the pairs of consecutive sides of the polygon, it is classified as concave or convex.
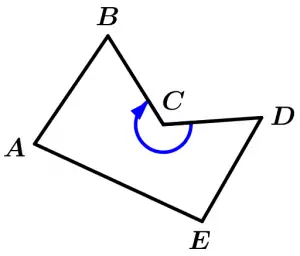
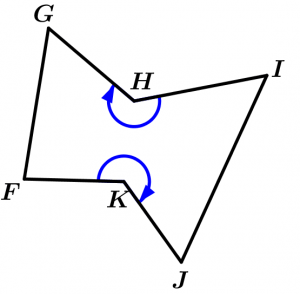
Concave polygons
When they contain one or more internal angles with measurements greater than 180°, they are called concave. It means that the concavity is observed from the outside of the polygon.
Concave polygon
Concave polygon
Convex polygons
They are convex when the measure of all the internal angles are less than 180°, implying that the convexity is observed from the outside of the polygon.
As you may have noticed, the concavity and convexity are observed from the outside of the polygons, so easy to know if a polygon is classified as concave or convex.
Classification according to the equality or inequality of angles and sides
What the title refers to is whether we have a regular polygon or if we have an irregular polygon.
Regular polygons
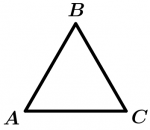
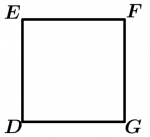
Regular polygons are those that have equal sides and equal angles, that is, they are equilateral and equiangular. There are times when we say that a polygon is equilateral is already regular, but be careful, as we mentioned: not all the equilateral polygons are regular, but all the regular polygons are equilateral. The same thing happens when we mention equiangular polygons: not all equiangular polygons are regular, but all regular polygons are equiangular. Let’s see some examples of regular polygons:
\text{Triangle } ABC \text{ is regular}
\text{Quadrilateral } DEFG \text{ is regular}
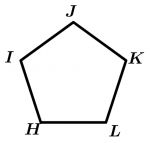
\text{Pentagon } HIJKL \text{ is regular}
Irregular polygons
Irregular polygons are those that have unequal sides, unequal angles, or both.
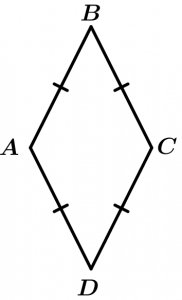
Let’s go with an example of a rhombus, this is an equilateral polygon because it has its equal sides, but it has unequal angles, therefore it is an irregular polygon:
The following example shows a quadrilateral that is equiangular, but is irregular, let’s see the rectangle:

Now let’s look at another example, a polygon that is not equiangular or equilateral, a simple quadrilateral:
The three figures mentioned above are irregular, we just wanted to emphasize that not because they are equilateral or equiangular are considered regular. The only figure that by force if it is equilateral, is equiangular and vice versa, that figure is the triangle.
Thank you for being at this moment with us :)