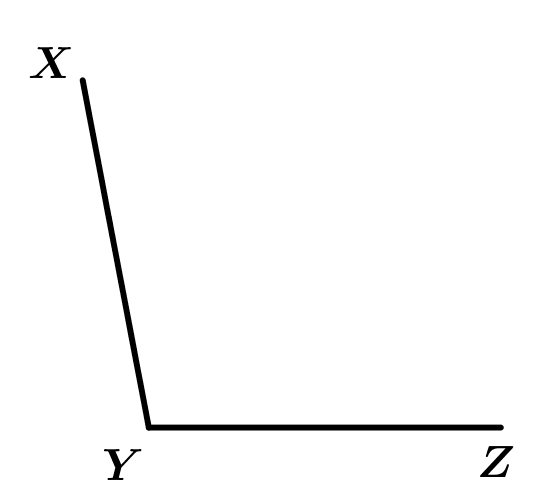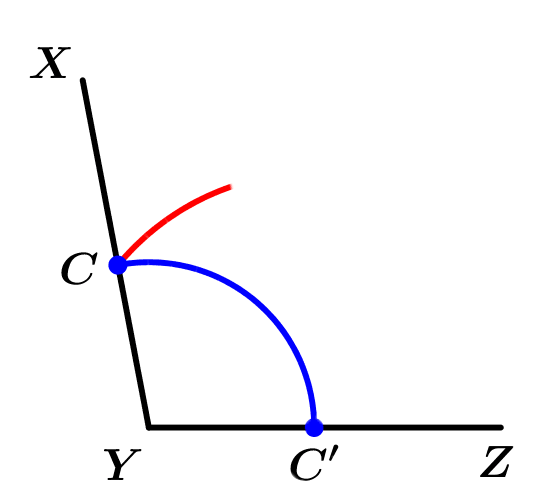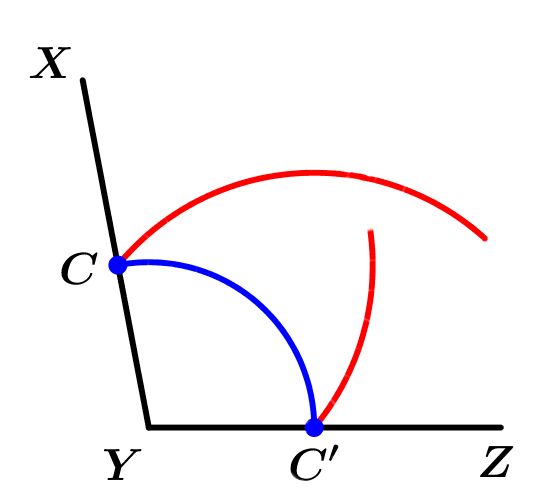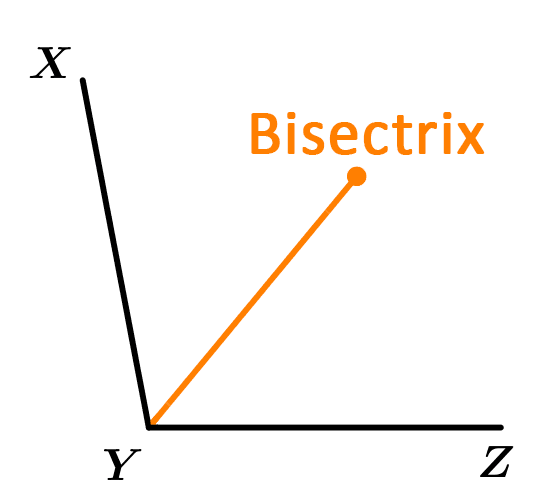The definition of bisectrix
It is called bisectrix from an angle to the line, ray or segment that divides this angle into two equal angles. The bisectrixes of the angles of a polygon that are cut at the same point is called incenter. All triangles have an incenter and not all polygons such as quadrilaterals, pentagons, hexagons, etc. have an incenter.
How to draw a bisectrix
Before continuing with the examples, I want to teach how to draw a bisectrix, you just need a compass. We will draw the bisectrix of \measuredangle XYZ.
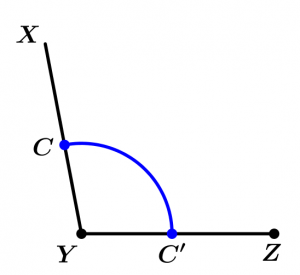
Next we will draw an arc of circumference where the point Y will be the center and the radius can be of the length that you like, thus we will obtain two intersections to which we will name C and C':
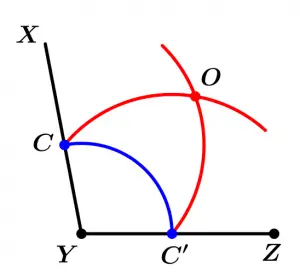
Then we will draw two more circumference arcs, which will have as centers C and C' and radius will be the segment \overline{C C'} and its intersection will be named O:
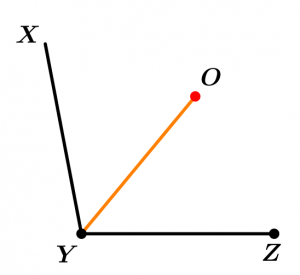
Finally, the segment, ray or line that is plotted with the points Y and O is the bisectrix.
Bisectrix of the \measuredangle XYZ
Graphically it is like this:
Let’s go with the examples of bisectrix
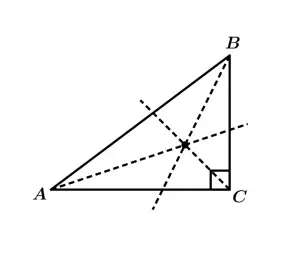
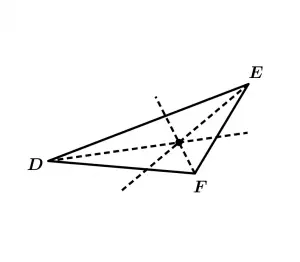
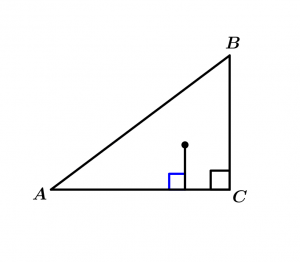
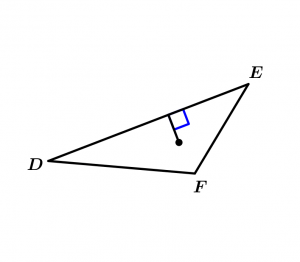
We will calculate the incenter of a triangle, to do this we must calculate the bisectrix of each angle of the triangle. We will work with a right triangle and with a scalene triangle.
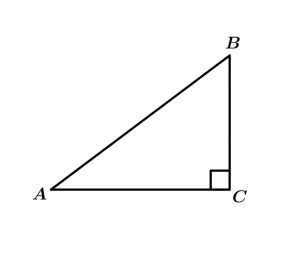
Right Triangle
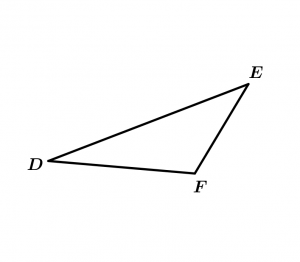
Scalene Triangle
\measuredangle ACB = 90^{\text{o}}
\overline{DE} \neq \overline{EF} \neq \overline{FD}
Now let’s draw the bisectors of each of the triangles:
Bisectrixes of the right triangle
Bisectrixes of the scalene triangle
Then we draw a segment that is perpendicular on any of the sides of the triangle, this segment will be the radius of our circumference:
Radius of the circumference inscribed in the right triangle
Radius of the circumference inscribed in the scalene triangle
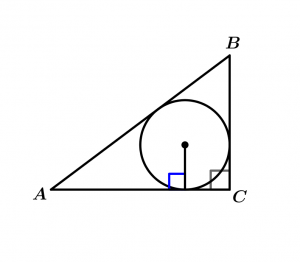
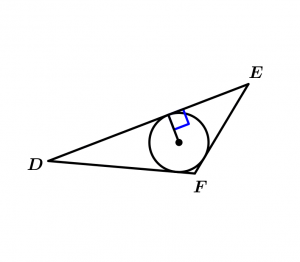
Now we simply draw our inscribed circle:
Circumference inscribed in a right triangle
Circumference inscribed in scalene triangle
That’s it, you know how to plot the incenter of any triangle.
Remember: if a polygon has an incenter, it has an inscribed circumference; if a polygon has an inscribed circle, it has an incenter.
Some more examples
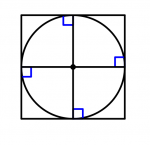
First I want to emphasize that ALL regular polygons have an incenter.
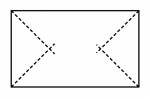
Next we will see some quadrilaterals. You will see that there are irregular quadrilaterals that have an incenter and others that do not. The dotted lines of the quadrilateral without incenter are the bisectors.
Regular quadrilateral with incenter
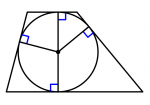
Irregular quadrilateral with incenter
Irregular quadrilateral without incenter
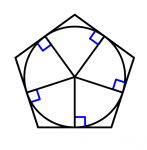
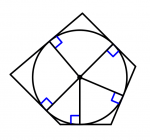
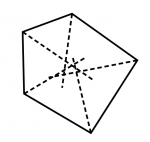
Next we will see some pentagons. You will see that there are irregular pentagons that have an incenter and others that do not. The dotted lines of the pentagon without incenter are the bisectors.
Regular pentagon with incenter
Irregular pentagon with incenter
Irregular pentagon without incenter
And as you may have noticed, all regular polygons have an incenter and there are irregular polygons that have and do not have an incenter.
You are ready to go out into the world and calculate bisectrixes and incenters!
Thank you for being at this moment with us : )