Calculate the arc length of 24xy = x^{4} + 48 from x = 2 to x = 4.
To solve this exercise, we will leave the y alone to be able to proceed with the derivative, so we have to spend dividing the 24x to obtain:
y = \cfrac{x^{4} + 48}{24x}
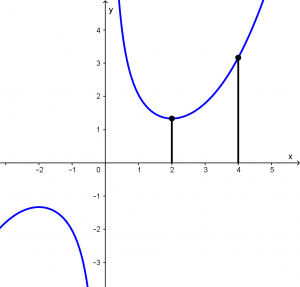
Now, it is advisable to graph the function to have a clearer length to calculate, so the graph will look like this:
Let’s divide the fraction of a sum into a sum of fractions and simplify:
y = \cfrac{x^{4}}{24x} + \cfrac{48}{24x}
y = \cfrac{x^{3}}{24} + \cfrac{2}{x}
Now we proceed with the derivative. The derivative of \frac{x^{3}}{24} equals \frac{x^{2}}{8} and the derivative of \frac{2}{x} is equal to -\frac{2}{x^{2}}:
y' = \cfrac{x^{2}}{8} - \cfrac{2}{x^{2}} = \cfrac{x^{4} - 16}{8x^{2}}
Now we can use the arc length formula to find that length, remember that the limits are from 2 to 4:
\displaystyle L = \int_{2}^{4}\sqrt{1 + \left[ \cfrac{x^{4} - 16}{8x^{2}} \right]^{2}} \ dx
We raise the square, we will obtain:
\displaystyle =\int_{2}^{4}\sqrt{1 + \cfrac{x^{8} - 32x^{4} + 256}{64x^{4}}}
Let’s make the sum of fractions (because the 1 has denominator 1) and simplify:
\displaystyle =\int_{2}^{4}\sqrt{\cfrac{64x^{4} + x^{8} - 32x^{4} + 256}{64x^{4}}}
\displaystyle =\int_{2}^{4}\sqrt{\cfrac{x^{8} + 32x^{4} + 256}{64x^{4}}}
We factor:
\displaystyle =\int_{2}^{4}\sqrt{\cfrac{\left( x^{4} + 16\right)^{2}}{64x^{4}}}
And we will take square root:
\displaystyle =\int_{2}^{4}\cfrac{x^{4} + 16}{8x^{2}}
Now, by properties of the integrals, we will extract the denominator 8 and then we will separate the integral of a sum in a sum of integrals:
\displaystyle =\cfrac{1}{8}\int_{2}^{4} \cfrac{x^{4} + 16}{x^{2}}
\displaystyle =\cfrac{1}{8} \int_{2}^{4} x^{2} \ dx + 2 \int_{2}^{4} \cfrac{dx}{x^{2}}
Let’s integrate, the integral of x^{2} is equal to \frac{x^{3}}{3} and the integral of \frac{1}{x^{2}} is equal to -\frac{1}{x}:
=\left. \cfrac{x^{3}}{24} - \cfrac{2}{x} \right]_{2}^{4}
Evaluating:
=\left( \cfrac{8}{3} - \cfrac{1}{2} \right) - \left(\cfrac{1}{3} - 1 \right)
Resolving the operations, we will obtain:
= \cfrac{17}{6} \ \text{u}
The \text{u} means units.
That’s how we get our final arc length result!
L = \cfrac{17}{6} \ \text{u} \approx 2.83 \ \text{u}
Thank you for being at this moment with us : )