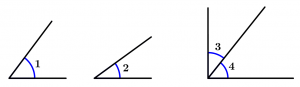
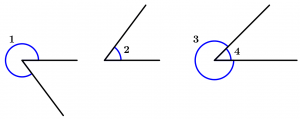An angle is the gap formed by two lines, rays or segments that share a point in common called vertex and according to their size and their grouping, we can classify them in two different ways.
Next we will see the types of angles according to their measure and according to their grouping.
Classification of the angles according to their measure
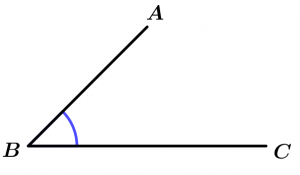
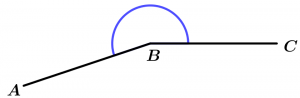
Acute angle
The acute angle is one that measures more than 0° and less than 90°.
0° < \ \measuredangle ABC < 90°
\measuredangle ABC \ \text{ is acute}
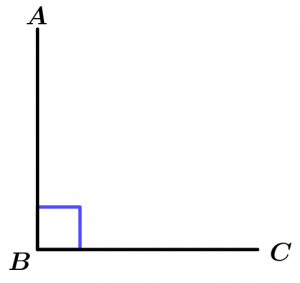
Right angle
The right angle is one that measures 90° and is usually symbolized by a small square at the corner of the angle.
\measuredangle ABC = 90°
\measuredangle ABC \ \text{ is right angle}
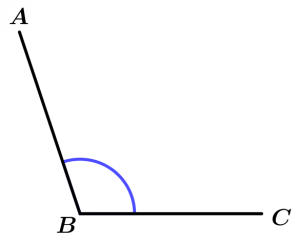
Obtuse angle
The obtuse angle is the one that measures more than 90° and less than 180°.
90° < \measuredangle ABC < 180°
\measuredangle ABC \ \text{ is obtuse}
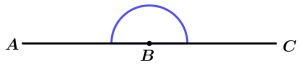
Straight angle
The straight angle is one that measures exactly 180°.
\measuredangle ABC = 180°
\measuredangle ABC \ \text{ is a straight angle}
Reflex angle
The reflex angle is one that measures more than 180° and less than 360°.
180° < \measuredangle ABC < 360°
\measuredangle ABC \ \text{ is reflex}
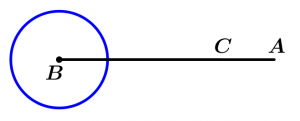
Full angle
The full angle is one that measures exactly 360°.
\measuredangle ABC= 360°
\measuredangle ABC \ \text{ is full angle}
Classification of the angles according to their grouping
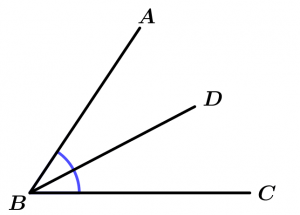
Adjacent angles
The adjacent angles are two angles that have one side and one vertex in common.
\measuredangle ABD \ \text{ is adjacent to } \ \measuredangle DBC
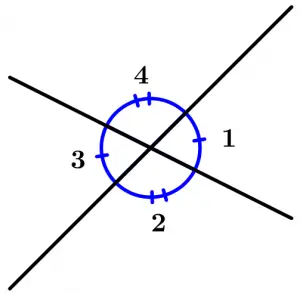
Opposite angles by the vertex
The angles opposite the vertex are those in which the sides of an angle are the extension of the sides of another angle and are also congruent.
\measuredangle 1 \ \text{ is opposite to } \ \measuredangle 3 \ \text{ and } \ \measuredangle 1 \cong \measuredangle 3
\measuredangle 4 \ \text{ is opposite to } \ \measuredangle 2 \ \text{ and } \ \measuredangle 4 \cong \measuredangle 2
Complementary angles
Complementary angles are two angles whose summed measures result in 90° and may be adjacent or not.
\measuredangle 1 + \measuredangle 2 = 90°
\measuredangle 3 + \measuredangle 4 = 90°
\measuredangle 1 \ \text{ and } \ \measuredangle 2 \ \text{ are not adjacent and }
\measuredangle 3 \ \text{ and } \ \measuredangle 4 \ \text{ are adjacent}
Supplementary angles
Supplementary angles are two angles whose summed measures result in 180° and may be adjacent or not.
\measuredangle 1 + \measuredangle 2 = 180°
\measuredangle 3 + \measuredangle 4 = 180°
\measuredangle 1 \ \text{ and } \ \measuredangle 2 \ \text{ are not adjacent and }
\measuredangle 3 \ \text{ and } \ \measuredangle 4 C\ \text{ are adjacent}
Conjugated angles
The conjugated angles are two angles whose summed measurements result in 360° and may be adjacent or not.
\measuredangle 1 + \measuredangle 2 = 360°
\measuredangle 3 + \measuredangle 4 = 360°
\measuredangle 1 \ \text{ and } \ \measuredangle 2 \ \text{ are not adjacent and }
\measuredangle 3 \ \text{ and } \ \measuredangle 4 \ \text{ are adjacent}
Thank you for being at this moment with us : )