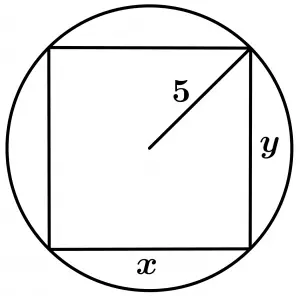
The statement of the calculation optimization exercise is the next:
Determine the area of the largest rectangle that can be inscribed in a circumference of 5 cm radius.
Let’s graph the rectangle and the circumference that the statement mentions:
Great, to continue with this exercise, let’s write the equation of the area of the rectangle:
A = xy
Now we will use the equation of the Pythagorean Theorem, with which our value of c will be the diameter of the circumference, resulting in the following:
x^{2} + y^{2} = 10^{2} = 100
As you want to determine the largest area of the rectangle, you have to derive the area of the rectangle, but it is not convenient to do so because the equation of the area of the rectangle has the unknown y. So what you have to do is take the equation we made with the Pythagorean theorem and isolate the term y, let’s see:
x^{2} + y^{2} = 100
We will subtract the x^{2}:
y^{2} = 100 - x^{2}
Now we apply square root to the whole equation to eliminate the square of the y:
y = \sqrt{100 - x^{2}}
Once we have the y single, we will replace it in the equation of the area of the rectangle:
A = xy
A = x\sqrt{100 - x^{2}}
And now we can start to derive, what is observed is that we have a multiplication, so what we have to do is apply the formula of the derivative of a multiplication, in any way here we remember the simple formula:
(ab)' = ab' + ba'
Now, let’s start to derive:
A' = \left(x\sqrt{100 - x^{2}}\right)'
A' = x\left( \sqrt{100 - x^{2}}\right)' + \sqrt{100 - x^{2}}(x)'
Using the algebra we can represent that \sqrt{100 - x^{2}} as \left( 100 - x^{2}\right)^{1/2} to make the derivative more simple and once we can derive x which is equal to 1:
A' = x\left( \left( 100 - x^{2}\right)^{1/2} \right)'+ \sqrt{100 - x^{2}}(1)
We will apply the chain rule:
A' = x\cfrac{1}{2}\left(100 - x^{2} \right)^{-1/2}(100 - x^{2})' + \sqrt{100 - x^{2}}
And now we just need to derive a single parenthesis, remember that we can divide that parenthesis as a sum of derivatives, then the derivative of 100 is equal to zero and the derivative of -x^{2} equals -2x:
A' = x \cfrac{1}{2} \left(100 - x^{2} \right)^{-1/2}(-2x) + \sqrt{100 - x^{2}}
Now that everything is already derived, you just need to apply a bit of algebra to simplify as much as possible:
A' = x \cfrac{1}{\cancel{2}} \ \cfrac{1}{(100 - x^{2})^{1/2}}(-\cancel{2}x) + \sqrt{100 - x^{2}}
A' = \cfrac{-x^{2}}{\sqrt{100 - x^{2}}}+ \sqrt{100 - x^{2}}
Let’s equalize to zero to find if there is a maximum in the derivative, because what you want is to obtain a greater amount of area:
\cfrac{-x^{2}}{\sqrt{100 - x^{2}}}+ \sqrt{100 - x^{2}} = 0
\cfrac{x^{2}}{\sqrt{100 - x^{2}}} = \sqrt{100 - x^{2}}
We pass multiplying to eliminate the square roots:
x^{2} = 100 - x^{2}
Now we will pass to the other side the -x^{2}
2x^{2} = 100
We will isolate dividing the 2
x^{2} = \cfrac{100}{2}
And using a calculator, we will calculate the square root of the equation:
x = \pm 5\sqrt{2}
Excellent, now let’s see where there is a maximum, remember that the test values have to be evaluated in the equation of the first derivative:
\begin{array}{| c | c | c | c |} \hline \text{Interval} & \text{Test value} & \text{Result sign} & \text{Conclusion} \\ \hline \left(-\infty,-5\sqrt{2}\right) & -8 & - & \text{decrease} \\ \left(-5\sqrt{2},5\sqrt{2}\right) & 0 & + & \text{increase} \\ \left(5\sqrt{2} ,\infty\right) & 8 & - & \text{decrease} \\ \hline \end{array}Note that in the second interval it grows and then in the third interval it decreases, meaning that this point is a maximum, so the value of x to be the highest is:
x = 5\sqrt{2}
Now we just need to calculate the value of y, which can be calculated using the equation when we have the y isolated and the value of x already calculated will replace it:
y = \sqrt{100 - x^{2}}
y = \sqrt{100 -\left( 5\sqrt{2} \right)^{2} }
y = \sqrt{100 - \left( 25(2) \right)}
y = \sqrt{100 - 50}
y = \sqrt{50}
Using a calculator, we have the following result:
y = 5\sqrt{2}
So the values of x and y so that the sides of the rectangle have the largest area inscribed in a circumference of a radius of 5 cm are:
x=5\sqrt{2} \qquad y = 5\sqrt{2}
Thank you for being at this moment with us : )