The integrals by trigonometric substitution seem to be difficult but with the following explanation we believe that they could be clear enough to master this style of integrals.
Three cases of the method of integration by trigonometric substitution are presented, we will see the explanation of each case and after each explanation we will show an example. Let’s get started!
First case of integrals by tri substitution
Explanation
When in an integral we have the form \sqrt{a^{2} - x^{2}}, the substitution of x = a \ \sin \theta will be used. Remembering that a will always have a value greater than zero. So:
\sqrt{a^{2} - x^{2}} \quad \Rightarrow \quad x = a \ \sin \theta
Example
Solve the following integral:
\displaystyle \int \cfrac{\sqrt{9 - x^{2}}}{x^{2}} \ dx
In the presented integral the value of a is not 9, the value of a is 3. You have to be careful with this because the first few times someone got confused with it. Great, once we have defined that a is 3, we are going to substitute the value of x:
x = 3 \sin \theta
Once we have the substitution, we have to find all the other elements of the integral with our substitution, we are going to square x and we are going to derive x. The derivative is:
dx = 3 \cos \theta \ d\theta
And x^{2} is:
x^{2} = 9 \sin^{2}\theta
Well, in order not to have to write all the elements of the integral so many times, we will take \sqrt{9-x^{2}}, substitute x^{2} and we will simplify it as much as we can, let’s see:
\sqrt{9 - x^{2}} = \sqrt{9 - 9 \sin^{2} \theta}
We will proceed to factor the 9:
=\sqrt{9\left( 1 - \sin^{2} \theta\right)}
Look! We know that trigonometric identity very well, we know that \cos^{2}\theta = 1 - \sin^{2} \theta, so we proceed to substitute in the root:
=\sqrt{9\cos^{2} \theta}
Applying square root to 9 results 3 and applying square root to \cos^{2}\theta results \cos \theta:
= 3 \cos \theta
Now we go back to our integral and substitute, remembering that \sqrt{9-x^{2}} = 3\cos \theta, x^{2} = 9 \sin^{2} \theta and dx = 3 \cos \theta \ d \theta:
\displaystyle \int \cfrac{\sqrt{9 - x^{2}}}{x^{2}} \ dx =\int \cfrac{3 \cos \theta}{9 \sin^{2} \theta}3 \cos \theta d \theta
We will cancel the 9 in the denominator with the 3 in the numerator and multiply the \cos \theta in the numerator:
\displaystyle = \int \cfrac{\cos^{2} \theta}{\sin ^{2} \theta} \ d \theta
Something very important to remember is that \cfrac{\cos \theta}{\sin \theta} = \cot \theta, so we will have:
\displaystyle = \int \cot^{2} \theta \ d \theta
At this point we will apply a trigonometric identity that says that \cot^{2} \theta = \csc^{2} \theta - 1:
\displaystyle = \int \left( \csc^{2} \theta - 1 \right) \ d \theta
The integral is almost solved, we will apply properties of integrals so that this subtraction of the integral becomes a subtraction of integrals:
\displaystyle = \int \csc^{2} \theta \ d \theta - \int d \theta
The integral of \csc^{2} \theta is equal to - \cot \theta and the integral of d \theta is equal to \theta, remember the + \text{ C}:
= -\cot \theta - \theta + \text{C}
We are almost done, using the trigonometric substitution of x = 3 \sin \theta, isolating the 3 we will get \cfrac{x}{3} = \sin \theta and remember that \sin \theta = \cfrac{\text{opposite leg}}{\text{hypotenuse}}, so our opposite leg is x and our hypotenuse is 3, the adjacent leg is the square root of the hypotenuse minus the square of the opposite leg. Let’s draw the following triangle to better locate everything mentioned in the paragraph:
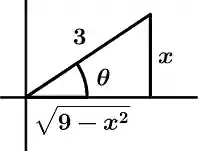
We know that x =3 \sin \theta, we have to isolate to leave \theta alone, resulting in:
\theta = \sin^{-1} \cfrac{x}{3}
And \cot \theta = \cfrac{\text{adjacent leg}}{\text{opposite leg}}, then:
\cot \theta = \cfrac{\sqrt{9 - x^{2}}}{x}
We substitute these (forgive the redundancy) substitutions in our result to finally obtain:
- \cfrac{\sqrt{9 - x^{2}}}{x^{2}} - \sin^{-1} \cfrac{x}{3} + \text{C}
Second case of integrals by trigonometric substitution
Explanation
When in an integral we have the form \sqrt{a^{2} + x^{2}}, the substitution of x = a \ \tan \theta will be used. Remembering that a will always have a value greater than zero. So:
\sqrt{a^{2} + x^{2}} \quad \Rightarrow \quad x = a \ \tan \theta
Example
Solve the following integral:
\displaystyle \int \sqrt{x^{2} + 5} \ dx
The value of a^{2} is equal to 5, so the value of a is \sqrt{5}, with this data we can now consider the trigonometric substitution:
x = \sqrt{5} \tan \theta
Now all you have to do is derive x and square x. Let’s derive first, derivative of \tan \theta is equal to \sec^{2} \theta \ d \theta:
dx = \sqrt{5} \sec^{2} \theta \ d\theta
And let’s square x:
x^{2} = 5 \tan^{2} \theta
Well, we’ll take the square root of the integral so we don’t have to write all the elements of the integral all the time, but you can do it however you like. Let’s continue, let’s make the substitution:
\sqrt{x^{2} + 5} = \sqrt{5\tan^{2} \theta + 5}
We will factor the 5:
=\sqrt{5\left(\tan^{2} \theta + 1 \right)}
Applying trigonometric identities, we can substitute \tan^{2}\theta + 1 for \sec^{2} \theta:
=\sqrt{5\sec^{2} \theta}
And we can apply square root so that \sec^{2} \theta be \sec \theta:
= \sqrt{5} \sec \theta
Since we have the substitution done, now let’s go to the integral and write what we just got and substitute dx = \sqrt{5}\sec^{2} \theta \ d \theta and \sqrt{x^{2} + 5} = \sqrt{5} \sec \theta:
\displaystyle \int \sqrt{x^{2} + 5} \ dx= \int\sqrt{5} \sec \theta \cdot \sqrt{5} \sec^{2} \theta \ d\theta
We will do the multiplication of the roots of 5 to obtain the value of 5 and we will multiply the secants to obtain the cubed secant, also by properties of the integrals we will extract at once from the integral the 5:
\displaystyle = 5 \int \sec^{3} \theta \ d\theta
Using a form, it can be seen that the integral of secant cubed is as follows:
\cfrac{1}{2} \sec \theta \tan \theta + \cfrac{1}{2} \ln \left|\sec \theta + \tan \theta \right| + \text{C}
So remembering that the integral was multiplied by 5, it will look like this:
\cfrac{5}{2} \sec \theta \tan \theta + \cfrac{5}{2} \ln \left|\sec \theta + \tan \theta \right| + \text{C}
Now we have to return the substitution to leave the result with terms of x, we need the triangle that has the values of the trigonometric substitution, remembering that x = \sqrt{5} \tan \theta we have the following triangle:
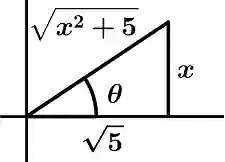
The triangle is constructed since as \tan \theta = \cfrac{\text{opposite leg}}{\text{adjacent leg}}, then \tan \theta = \cfrac{ x}{\sqrt{5}}, that means that x is the value of the opposite leg and \sqrt{5} is the value of the adjacent leg and the value of the hypotenuse is calculated as the root of the sum of the squares of the legs or more briefly, with the Pythagorean Theorem: c^{2} = a^{2} + b^{2}.
Since we have the triangle, we can proceed to substitute:
\sec\theta = \cfrac{\text{hypotenuse}}{\text{adjacent leg}}
\sec \theta = \cfrac{\sqrt{x^{2} + 5}}{\sqrt{5}}
Now we go with tangent of theta:
\tan \theta = \cfrac{\text{opposite leg}}{\text{adjacent leg}}
\tan \theta = \cfrac{x}{\sqrt{5}}
Great, we already have all the calculations done, now we can move on to substituting in the result:
=\cfrac{5}{2} \left( \cfrac{\sqrt{x^{2} + 5}}{\sqrt{5}} \right) \left( \cfrac{x}{\sqrt{5}} \right) + \cfrac{5}{2}\ln \left|\cfrac{\sqrt{x^{2} + 5}}{\sqrt{5}} + \cfrac{x}{\sqrt{5}} \right| + \text{C}
Let’s reduce terms:
\cfrac{x\sqrt{x^{2} + 5}}{2} + \cfrac{5}{2} \ln \left|\cfrac{x + \sqrt{x^{2} + 5}}{\sqrt{5}} \right| + \text{C}
The logarithm of the division can be separated as a subtraction of logarithms:
\cfrac{x\sqrt{x^{2} + 5}}{2} + \cfrac{5}{2} \ln \left| x + \sqrt{x^{2} + 5} \right| - \cfrac{5}{2} \ln \sqrt{5} + \text{C}
Here you can do a “trick” to reduce terms, the term of \frac{5}{2} \ln \sqrt{5} is a constant, it can be added to \text{C} since \frac{5}{2} \ln \sqrt{5} is a constant just like \text{C}, observe how our final result of the integral will look like:
= \cfrac{x\sqrt{x^{2} + 5}}{2} + \cfrac{5}{2} \ln \left|x + \sqrt{x^{2} + 5} \right| + \text{C}
Third case of trigonometric integration substitution
Explanation
When in an integral we have the form \sqrt{x^{2} - a^{2}}, the substitution of x = a \ \sec \theta will be used. Remembering that a will always have a value greater than zero. So:
\sqrt{x^{2} - a^{2}} \quad \Rightarrow \quad x = a \ \sec \theta
Example
Solve the following integral:
\displaystyle \int \cfrac{dx}{x^{3}\sqrt{x^{2} - 9 }}
Before continuing I want to make a clarification, note that this time the root is in the denominator and multiplied by a cubic X, I want to clarify that it does not matter if the root is in the numerator or in the denominator, as long as it has the shape of the root to perform the substitution you can do the substitution, there is no rule that the root needs to be in the denominator or the numerator to do that. As long as it has the form of the root of any case of trigonometric substitution, the case that is required can be applied. Let’s continue.
The value of a^{2} is equal to 9, so the value of a is 3, With this data we can now consider the trigonometric substitution:
x = 3\sec \theta
We have to derive x, square and cube x, let’s derive first:
dx = 3 \sec \theta \tan \theta \ d \theta
The square of x is:
x^{2} = 9\sec^{2} \theta
And the cube of x is:
x^{3} = 27 \sec^{3} \theta
We will take the square root to reduce it as much as possible, this is only done so as not to have to write the other elements of the integral every so often, let’s continue:
\sqrt{x^{2} - 9} = \sqrt{9\sec^{2} \theta - 9}
Let’s factor the 9:
=\sqrt{9\left( \sec^{2} \theta - 1\right)}
Now what can be seen is that we have a trigonometric identity, which tells us that \tan^{2}\theta = \sec^{2} \theta - 1, let’s substitute:
=\sqrt{9 \tan^{2} \theta}
We take square root and done, square root of 9 is 3 and square root of \tan^{2}\theta is \tan \theta:
= 3 \tan \theta
Great, with this substitution we’re going to replace all x and simplify, dx = 3\sec\theta \tan \theta \ d \theta, x^{ 3} = 27\sec^{3} \theta and \sqrt{x^{2} - 9} = 3\tan \theta:
\displaystyle \int\cfrac{dx}{x^{3}\sqrt{x^{2} - 9}} = \int \cfrac{3 \sec \theta \tan \theta \ d \theta}{27\sec^{3}\theta \left( 3\tan \theta\right)}
Let’s simplify, the 3 of the numerator cancels with the 3 of the denominator, the secant cubed becomes secant squared and the secant of the numerator cancels, the tangent of the numerator is canceled with the tangent of the denominator and by properties of integrals we will remove \frac{1}{27} from the integral, let’s see:
\displaystyle = \cfrac{1}{27} \int \cfrac{d\theta}{\sec^{2} \theta}
Knowing the trigonometric functions, \frac{1}{\sec^{2}\theta} = \cos^{2} \theta, so our integral will look like this:
\displaystyle = \cfrac{1}{27} \int \cos^{2} \theta \ d \theta
At this moment we have to apply trigonometric identities to be able to solve the integral, see what \cos^{2}\theta is equal to thanks to the trigonometric identities:
\cos^{2} \theta = \cfrac{1}{2} + \cfrac{1}{2} \cos 2\theta
We substitute it in the integral:
\displaystyle = \cfrac{1}{27} \int \left( \cfrac{1}{2} + \cfrac{1}{2} \cos 2\theta\right) \ d \theta
By properties of the integrals we will separate that sum of the integral in a sum of integrals and at once we will multiply the 2 with the 27:
\displaystyle =\cfrac{1}{54}\int d \theta + \cfrac{1}{54} \int \cos 2 \theta \ d \theta
The integral of d\theta is \theta:
\displaystyle =\cfrac{1}{54}\theta + \cfrac{1}{54} \int \cos 2\theta \ d \theta
To solve the missing integral we have to make a change of variable, we will use u instead of 2\theta, we only need to derive u:
u = 2\theta
du = 2 d \theta
We pass dividing the 2:
\cfrac{du}{2} = d \theta
And now we substitute the variables into the integral. (For the moment we will not write the result obtained from \frac{1}{54}\theta, we will rewrite it later):
\displaystyle = \cfrac{1}{54} \int \cos u \ \cfrac{du}{2}
Due to the properties of integrals, we will extract the 2 so that it multiplies 54 and at once we apply the cosine integral that is equal to sine:
=\cfrac{1}{108} \sin u
We substitute back the 2\theta:
=\cfrac{1}{108} \sin 2\theta
We rewrite the other result that we left out and remember to put the +\text{C}:
=\cfrac{1}{54} \theta + \cfrac{1}{108}\sin 2\theta + \text{C}
Let’s apply another trigonometric identity which says that \sin 2\theta = 2\sin \theta \cos \theta, let’s substitute:
\cfrac{1}{54} \theta + \cfrac{1}{108}\left( 2\sin \theta \cos \theta\right)
Let’s simplify:
\cfrac{1}{54} \theta + \cfrac{1}{54}\sin \theta \cos \theta + \text{C}
And now, to leave the result in terms of x, we need the triangle that will tell us everything, remembering that x = 3 \sec \theta, \sec \theta = \cfrac{\text{hypotenuse}}{\text{adjacent leg}} so the hypotenuse will be x and the adjacent leg will be 3 , the opposite leg of \theta will be the square root of the hypotenuse minus the square of the adjacent leg, let’s look at the triangle:
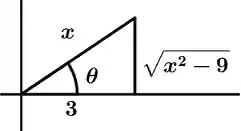
Since we already have x = 3\sec \theta, we have to isolate \theta, so we pass by dividing 3 into x and \frac{x}{3} = \sec \theta will be obtained, applying inverse secant to equality we will obtain the value of \theta:
\theta = \sec^{-1}\cfrac{x}{3}
Remember that \sin \theta = \cfrac{\text{opposite leg}}{\text{hypotenuse}}, looking at the triangle:
\sin \theta = \cfrac{\sqrt{x^{2} - 9}}{x}
Remembering that \cos \theta = \cfrac{\text{adjacent leg}}{\text{hypotenuse}}, observing the triangle we will obtain that:
\cos \theta = \cfrac{3}{x}
So, substituting all the values, we have our final result:
=\cfrac{1}{54} \sec^{-1}\cfrac{x}{3} + \cfrac{1}{18} \left( \cfrac{\sqrt{x^{2} - 9}}{x^{2}} \right) + \text{C}
Thank you for being in this moment with us : )
