In this article we will explain the calculation of the area between a cardioid and a circumference using double integrals, let’s start!
We will begin by writing the function and the graph of our cardioid and our circumference.
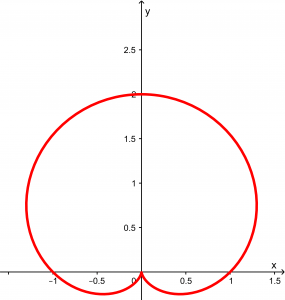
Our cardioid has the following graph and function:
r= 1+ \sin \theta
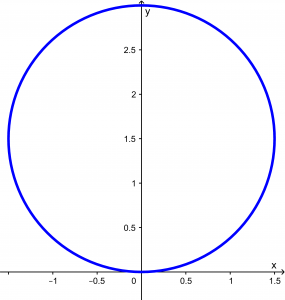
And our circumference has the following function and graph:
r=3 \sin \theta
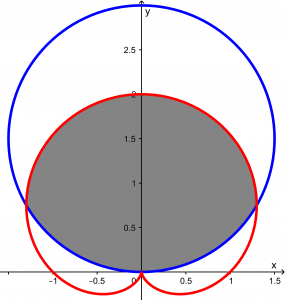
Now joining the two graphs, we will have:
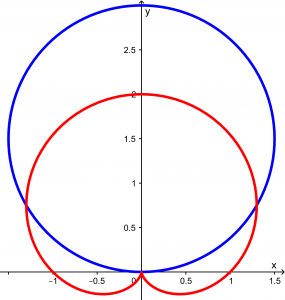
And the area we want to calculate is the shaded area shown in the following figure:
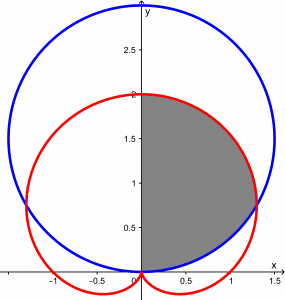
Observing the graph, you can see that it is symmetric, so to make life easier, we will calculate only the area of the half and the result will be multiplied by 2. We will calculate this area:
Observing the graphs, what we will have to do is a resolution of a sum of double integrals, why? Because first we are going to calculate the area above and below the intersection angle. Let’s start by calculating the angle at which they intersect.
But how is the angle at which they are intercepted calculated? Easy, let’s match the function of the circumference with the function of the cardioid:
3\sin\theta = 1 + \sin \theta
Now what we proceed to do is the resolution of the equality to find the angle \theta, so we will subtract the \sin \theta to 3\sin \theta:
3\sin \theta - \sin \theta = 1
2\sin \theta = 1
Now we proceed to pass dividing the 2:
\sin \theta = \cfrac{1}{2}
And finally to find \theta we apply the inverse sine on both sides of the equality and what will happen is that the sine we already have will be canceled with the inverse sine and the \frac{1}{2} will be \sin^{- 1}\left (\frac{1}{2}\right):
\sin^{-1}\left(\sin \theta\right) = \sin^{-1}\left( \cfrac{1}{2}\right)
\theta = \sin^{-1} \left( \cfrac{1}{2}\right)
We can directly use the calculator in the inverse sine in radian mode to determine the value of \theta, which results in the following:
\theta = \cfrac{\pi}{6}
Excellent, we already have the angle in radians in which the two functions are intercepted. Now we can raise our sum of double integrals.
We will raise our first double integral that is below \frac{\pi}{6}, that means that the radius will be from zero to the function 3\sin \theta:
\displaystyle \int_{0}^{\frac{\pi}{6}} \int_{0}^{3\sin \theta}r \ dr \ d\theta
Now, our second double integral is above \frac{\pi}{6}, that means that the radius will be from zero to the function 1+\sin \theta, and also the integration angle goes from \frac{\pi}{6} to \frac{\pi}{2}.
But why up to \frac{\pi}{2}? Because \frac{\pi}{2} means that the angle will be 90°, which is half the area we want to calculate. Well, let’s pose the second integral:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\int_{0}^{1 + \sin \theta}r \ dr \ d\theta
Well, we already have our two integrals raised, we will proceed to solve the first integral of the first double integral.
First double integral
\displaystyle \int_{0}^{\frac{\pi}{6}}\int_{0}^{3\sin \theta}r \ dr \ d\theta
Integrating we will have as a result the following:
\displaystyle \int_{0}^{\frac{\pi}{6}}\left.\cfrac{r^{2}}{2} \right|_{0}^{3\sin \theta} \ d \theta
We evaluate:
\displaystyle \int_{0}^{\frac{\pi}{6}}\left(\cfrac{(3\sin \theta)^{2}}{2} - \cfrac{(0)^{2}}{2}\right) \ d \theta
\displaystyle \int_{0}^{\frac{\pi}{6}}\cfrac{9\sin^{2}\theta}{2} \ d \theta
Applying properties of the integrals we will extract the \frac{9}{2} from the integral:
\displaystyle \cfrac{9}{2}\int_{0}^{\frac{\pi}{6}}\sin^{2}\theta \ d\theta
In order to solve the previous integral, we have to apply the following trigonometric identity:
\sin^{2}\theta = \cfrac{1}{2} - \cfrac{1}{2}\cos 2 \theta
With which our integral will be as follows:
\displaystyle \cfrac{9}{2}\int_{0}^{\frac{\pi}{6}} \left( \cfrac{1}{2} - \cfrac{1}{2} \cos 2\theta\right) d\theta
Now applying property of integrals, we will separate the integral of a sum in a sum of integrals:
\displaystyle \cfrac{9}{2} \int_{0}^{\frac{\pi}{6}}\cfrac{1}{2} \ d\theta - \cfrac{9}{2} \int_{0}^{\frac{\pi}{6}} \cfrac{1}{2} \cos 2 \theta \ d \theta
Applying properties of integrals, we will extract the fractions of \frac{1}{2} from the integrals and multiply the fractions of \frac{9}{2}:
\displaystyle \cfrac{9}{4}\int_{0}^{\frac{\pi}{6}} \ d \theta - \cfrac{9}{4} \int_{0}^{\frac{\pi}{6}}\cos 2 \theta \ d \theta
How to solve the integral of \cos 2 \theta \ d \theta? We have to make a variable change, let’s see how it is done. We will substitute u with 2\theta, we will derive and clear:
u = 2 \theta
du = 2 d\theta
\cfrac{du}{2} = d\theta
Now we substitute all the variables that have \theta of the integral of \cos 2 \theta \ d \theta, it would be as follows:
\displaystyle \cfrac{9}{4}\int_{0}^{\frac{\pi}{6}} \ d\theta - \cfrac{9}{4} \int_{0}^{\frac{\pi}{6}} \cos u \cfrac{du}{2}
We will integrate the integral of the left and we will apply property of integrals in the integral of \cos u \ \cfrac{du}{2} to take out the \frac{1}{2} from the integral and multiply it with \frac{9}{4}:
\displaystyle \left.\cfrac{9}{4} \ \theta \right |_{0}^{\frac{\pi}{6}} - \cfrac{9}{8}\int_{0}^{\frac{\pi}{6}}\cos (u) \ du
We will substitute terms in \frac{9}{4}\theta and we will solve the integral of \cos u \ du. Remember that the integral of \cos u equals to \sin u:
\cfrac{9}{4}\left( \cfrac{\pi}{6} \right) - \cfrac{9}{4}(0) - \cfrac{9}{8} \left[ \left.\sin(u)\right|_{0}^{\frac{\pi}{6}} \right]
We multiply and add what can be solved and we will substitute the u for the 2\theta back:
\cfrac{9\pi}{24} - \cfrac{9}{8}\left[ \left. \sin(2\theta) \right|_{0}^{\frac{\pi}{6}} \right]
Now we will evaluate the \sin 2 \theta, you can use a calculator:
\cfrac{9\pi}{24} - \cfrac{9}{8}\left[ \sin\left(2\cfrac{\pi}{6}\right) - \sin(2(0))\right]=
\cfrac{9\pi}{24} - \cfrac{9}{8}\left[ \cfrac{\sqrt{3}}{2} - 0 \right]
Finally, the result of our first double integral will be:
\cfrac{9\pi}{24} - \cfrac{9\sqrt{3}}{16}
Now let’s proceed with our second double integral
Relax, doing it by hand and with practice you can skip many steps, cheer up!
Let’s rewrite our second double integral:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\int_{0}^{1 + \sin \theta}r \ dr \ d\theta
Solving the integral of r\ dr, we would have the following:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left.\cfrac{r^{2}}{2}\right|_{0}^{1 + \sin \theta}\ d\theta
We evaluate:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left[\cfrac{(1 + \sin \theta)^{2}}{2} - \cfrac{(0)^{2}}{2}\right] \ d\theta
We will solve and we will have as a result the following:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left[ \cfrac{(1 + \sin \theta)^{2}}{2}\right] \ d \theta
We will apply integral properties to extract the \frac{1}{2} from the integral:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}(1 + \sin \theta)^{2} \ d \theta
Now we will make the binomial squared:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left( 1 + 2 \sin \theta + \sin^{2} \theta \right) \ d \theta
Applying properties of the integrals, we will make the integral of a sum, be a sum of integrals:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \ d \theta + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} 2 \sin \theta \ d \theta + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \sin^{2} \theta \ d \theta
Applying more properties of integrals, we will take out the 2 from the integral of 2\sin \theta \ d \theta to obtain the following:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \ d \theta + \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \sin \theta \ d \theta + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \sin^{2} \theta \ d \theta
The integral of d\theta and the integral of \sin \theta \ d \theta are solved very easy, we will solve them at once. First let’s remember that the integral of \sin \theta is equal to -\cos \theta , now yes:
\displaystyle \cfrac{1}{2}\left[\left. \theta\right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\right] + \left[- \left. \cos \theta \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\right] + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\sin^{2}\theta d \theta
Now we evaluate:
\displaystyle \cfrac{1}{2} \left[ \cfrac{\pi}{2} - \cfrac{\pi}{6}\right] + \left[ -\cos\left( \frac{\pi}{2} \right)- \left(-\cos\left( \frac{\pi}{6} \right) \right)\right] + \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\sin^{2}\theta \ d \theta
You can use a calculator to solve the cosine evaluations and then simplify everything that can be simplified:
\displaystyle \cfrac{1}{2} \left[ \cfrac{\pi}{3} \right] + \left[ 0 - \left(-\cfrac{\sqrt{3}}{2}\right)\right]+\cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\sin^{2}\theta \ d\theta =
\displaystyle \cfrac{\pi}{6} + \cfrac{\sqrt{3}}{2} + \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\sin^{2}\theta \ d\theta
Let’s leave a checkpoint here.
Now, for the moment we proceed to solve the integral of \sin^{2} \theta \ d \theta. It is easy to solve it, you just have to know the following trigonometric identity:
\sin^{2} \theta = \cfrac{1}{2} - \cfrac{1}{2}\cos(2\theta)
Substituting in the integral, it will be as follows:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left( \cfrac{1}{2} - \cfrac{1}{2} \cos 2 \theta\right) \ d \theta
Applying properties of integrals, we will make the integral of a sum in a sum of integrals:
\displaystyle \cfrac{1}{2} \int _{\frac{\pi}{6}}^{\frac{\pi}{2}}\cfrac{1}{2} \ d \theta + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}-\cfrac{1}{2}\cos 2 \theta \ d \theta
Applying properties of integrals, we will extract the negative sign of the integral and also the fractions of \frac{1}{2} and proceed to multiply them with the fractions of \frac{1}{2} that we already had:
\displaystyle \cfrac{1}{4} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\ d \theta - \cfrac{1}{4} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos 2 \theta \ d\theta
To solve the integral of \cos 2\theta \ d \theta, you have to make a variable change of u for 2\theta, derive and clear:
u = 2 \theta
du = 2 \ d \theta
\cfrac{du}{2} = d \theta
Now, let’s substitute all the \theta‘s in the integral of cosine:
\displaystyle \cfrac{1}{4}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \ d \theta - \cfrac{1}{4} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos(u) \cfrac{du}{2}
Applying properties of integrals, we will extract the \frac{1}{2} from the integral of cosine and multiply it with the \frac{1}{4}:
\displaystyle \cfrac{1}{4}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \ d \theta - \cfrac{1}{8} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos (u) \ du
Now we can easily solve the two integrals, remember that the integral of \cos u equals \sin u:
\cfrac{1}{4} \left[ \left. \theta \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}} \right] - \cfrac{1}{8}\left[ \left. \sin u \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\right]
We return the variable change from u to 2\theta:
\cfrac{1}{4} \left[ \left. \theta \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}} \right] - \cfrac{1}{8}\left[ \left. \sin 2\theta \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\right]
You can use a calculator to support you in the breast evaluation:
\cfrac{1}{4}\left[ \cfrac{\pi}{2} - \cfrac{\pi}{6}\right] - \cfrac{1}{8} \left[ \sin\left( \cfrac{2\pi}{2}\right) - \sin \left( \cfrac{2\pi}{6} \right)\right]=
\cfrac{1}{4}\left[ \cfrac{\pi}{3} \right]-\cfrac{1}{8} \left[ 0 - \cfrac{\sqrt{3}}{2}\right]
We multiply what can be multiplied and add what can be added:
\cfrac{\pi}{12} + \cfrac{\sqrt{3}}{16}
With the result obtained, we return to our checkpoint to add the result obtained from the other integrals:
\cfrac{\pi}{6} + \cfrac{\sqrt{3}}{2} + \cfrac{\pi}{12} + \cfrac{\sqrt{3}}{16}
Simplifying, we will obtain the following result:
\cfrac{\pi}{4} + \cfrac{9\sqrt{3}}{16}
Almost!
We have the result of our first double integral and the result of our second double integral, we proceed simply to add the two results:
\cfrac{9\pi}{24} - \cfrac{9\sqrt{3}}{16}+\cfrac{\pi}{4} + \cfrac{9\sqrt{3}}{16}
We solve and our result will be:
\cfrac{5}{8} \pi
FINALLY
Now the result obtained we have to multiply by 2 because we only find the area of the half of the graph because it is symmetric, so the final result is:
\cfrac{5}{4}\pi \ \text{u}^{2}
Thank you for being at this moment with us : )