Hi all!
The example that we will do is a very beautiful subject of Calculus that is the determination of the area of a cardioid inside a circumference. Remember that if you are going to use the calculator, you have to place it in radian mode.
Graphic of a cardioid
The equation of a cardioid r=1+\cos \theta is displayed as shown below:
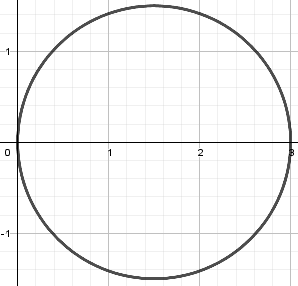
Graph of the circumference
The equation of the circumference r=3\cos \theta is displayed as shown below:
So what is the area we are looking for?
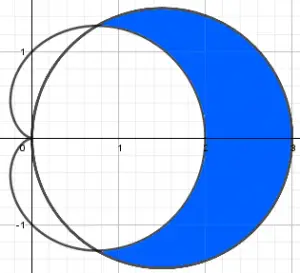
The area is the one that is limited by the cardioid and the circumference, which is painted blue in the following figure:
We solve with double integrals
For the resolution of the exercise we will use double integrals, which would be represented as follows:
\displaystyle \int_{0}^{\frac{\pi}{3}} \int_{1 + \cos \theta}^{3 \cos \theta}r dr d\theta
Explaining each part of the integral:
First integral limited by the radius of the circumference and the cardioid
The integral of r \ dr means the radius, therefore we are integrating the radius, which radius has a lower limit of 1+\cos \theta corresponding to the radius of the cardioid and a higher radius of 3\cos \theta corresponding to the radius of the circumference.
Second integral limited by the points of intersection of the circumference and the cardioid
The second integral of d\theta is of the angle limits we are going to integrate, in this case, we are going to integrate from angle 0° to the angle of 60° or \cfrac{\pi}{3}. Where did that \cfrac{\pi}{3} come from? It will be explained below:
We match the two curves that we have that are the cardioid and the circumference to determine the angle \theta:
1 + \cos \theta = 3 \cos \theta
Isolate the \cos\theta to subtract it:
1 = 2 \cos \theta
We divide the 1 with the 2:
\cfrac{1}{2} = \cos \theta
We apply \cos^{-1} to all equality:
\cos ^{-1}\left(\cfrac{1}{2}\right) = \theta
And finally we found the angle of \theta, we can use the calculator:
\theta = \cfrac{\pi}{3}
And that’s the explanation why the integration limits go from 0 to\frac{\pi}{3}.
Note:
The result obtained at the end will have to be multiplied by 2 because only the top part of the horizontal axis has been found.
We perform the whole integration process
\displaystyle \int_{0}^{\frac{\pi}{3}} \int_{1 + \cos \theta}^{3 \cos \theta}r dr d\theta
Integral of r
Integrate the r\ dr with its respective limits and it would be as follows:
\left . \cfrac{r^{2}}{2} \right |_{1+ \cos \theta}^{3 \cos \theta}
Do the substitution:
\cfrac{(3 \cos \theta)^{2} - (1 + \cos \theta)^{2}}{2}
Break down the binomial to the square:
\cfrac{9 \cos^{2} \theta \ - (1 + 2 \cos \theta + \cos^{2} \theta)}{2}
Simplify terms:
\cfrac{8 \cos^{2} \theta \ - 2 \cos \theta \ - 1}{2} = 4 \cos^{2}\theta \ - \cos \theta -\cfrac{1}{2}
Integral of \theta
Now the integral with respect to \theta will be as follows:
\displaystyle \int_{0}^{\frac{\pi}{3}}\left(4 \cos^{2}\theta \ - \cos \theta \ -\frac{1}{2}\right) \ d\theta
Applying properties of the integrals, separate the integrals to have 3 integrals:
\displaystyle 4 \int_{0}^{\frac{\pi}{3}}cos^{2}\theta \ d\theta \ - \int_{0}^{\frac{\pi}{3}} \cos \theta \ d\theta \ - \frac{1}{2}\int_{0}^{\frac{\pi}{3}} \ d\theta
To solve the integral we need the following trigonometric identity:
\cos^{2}\theta = \cfrac{1}{2}\cos 2 \theta + \cfrac{1}{2}
And with this, it turns out that now we will have 4 integrals:
\displaystyle 4 \int_{0}^{\frac{\pi}{3}} \frac{1}{2} \cos 2\theta \ d\theta + 4\int_{0}^{\frac{\pi}{3}}\frac{1}{2} \ d\theta \ - \int_{0}^{\frac{\pi}{3}} \cos \theta \ d\theta- \frac{1}{2}\int_{0}^{\frac{\pi}{3}} \ d\theta
Look at \displaystyle 4 \int_{0}^{\frac{\pi}{3}} \cfrac{1}{2} \cos 2\theta \ d\theta
We are going to reduce terms of that integral:
\displaystyle 2 \int_{0}^{\frac{\pi}{3}} \cos 2\theta \ d\theta
Now let’s make variable changes:
u = 2\theta
Derived:
du = 2 \ d\theta
Leave the d \theta alone:
\cfrac{du}{2} = d \theta
And now the integral would be as follows:
\displaystyle 2\int_{0}^{\frac{\pi}{3}} \cos u \frac{du}{2}
Cancel the 2 that appear:
\displaystyle \int_{0}^{\frac{\pi}{3}} \cos u \ du
Apply the formula that says:
\displaystyle \int \cos u \ du= \sin u \ du
Thus:
\displaystyle \int_{0}^{\frac{\pi}{3}} \cos u \ du = \left . \sin u \right |_{0}^{\frac{\pi}{3}}
Remember that u=2 \ \theta, it would look like:
\left . \sin 2 \ \theta \right |_{0}^{\frac{\pi}{3}}
Reordering all the terms of the equation!
Reordering all the terms we have seen, it would be as follows:
\displaystyle \left . \sin 2 \theta \right |_{0}^{\frac{\pi}{3}} + 2 \int_{0}^{\frac{\pi}{3}} \ d\theta \ - \int_{0}^{\frac{\pi}{3}}\cos \theta \ d\theta \ - \frac{1}{2} \int_{0}^{\frac{\pi}{3}} \ d\theta
Remembering that \displaystyle \int\ d \theta = \theta , we will do all the missing integrals:
\left [ \sin 2 \theta + 2 \theta \ - \sin \theta \ - \cfrac{1}{2} \theta \right ]_{0}^{\frac{\pi}{3}}
How everything will be evaluated from 0 to \frac{\pi}{3}, the expression would be as follows:
\sin (\cfrac{2\pi}{3}) + \cfrac{2\pi}{3} - \sin (\cfrac{\pi}{3}) - \cfrac{1}{2}(\cfrac{\pi}{3})
We can use a calculator and enter all the values and we will obtain the following:
\cfrac{\sqrt{3}}{2} + \cfrac{2\pi}{3} - \cfrac{\sqrt{3}}{2} - \cfrac{\pi}{6} = \cfrac{\pi}{2}
But remember that we only find the upper part of the abscissa axis, so the result has to be multiplied by 2.
Therefore the final result of the cardioid area within the circumference is equal to:
A = \pi u ^{2}
Thank you for being at this moment with us : )