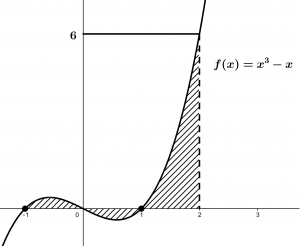
The following example of the definite integral is:
Find the integral of f(x)=(x^{3}-x) within the limits of -1 to 2:
\displaystyle \int_{-1}^{2}(x^{3} - x) dx
In this example of definite integral we are going to sketch the function only to have it visually, to be able to do that we are going to factor and equalize the function to zero and we will find the points of intersection:
0 = (x^{3}-x)
0 = x(x^{2}-1)
As you can see, we have a point of intersection at zero and the other two points of intersection we have in 1 and a -1:
x = 0 \qquad x = 1 \qquad x = -1
Now that we have the points of intersection of the function of the definite integral, we will sketch it and shading the area to be found within the limits that the integral tells us:
Great, now that we have sketched the function, we will proceed with the integral, we can consult here to resort to the formulas of the integrals:
\displaystyle \int_{-1}^{2}(x^{3} - x) \ dx = \cfrac{x^{4}}{4} - \cfrac{x^{2}}{2} = \cfrac{x^{2} - 2x^{2}}{4}
Now we will continue with the evaluation of the limits:
= \left. \cfrac{x^{4} - 2x^{2}}{4} \right]_{-1}^{2}
\begin{array}{c c c}
\text{We evaluate in }2 & \qquad & \text{We evaluate in} -1 \\
\cfrac{(2)^{4} - 2(2)^{2}}{4} = 2& & \cfrac{(-1)^{4} - 2(-1)^{2}}{4} = -\cfrac{1}{4}
\end{array}We solve some simple operations:
2 -\left(- \cfrac{1}{4} \right)= 2 + \cfrac{1}{4}
And so we get that the shaded area is equal to:
\cfrac{9}{4}u^{2}
Let’s check the definite integral with the Riemann summation limit
To be able to check a definite integral with a Riemann summation, what must be remembered are the following formulas:
\displaystyle A = \underset{n \to \infty} \lim \; \sum_{i = 1}^{n} f(c_{i})\Delta x
\Delta x = \cfrac{b - a}{n}
c_{i} = x_{i} = a + i\Delta x
The value of a is the lower limit of the integral and b is the value of the upper limit of the same integral. First let’s find the value of \Delta x:
\Delta x = \cfrac{2 - (-1)}{n} = \cfrac{3}{n}
Once we have \Delta x, we are going to find c_{i}:
c_{i} = -1 + i\Delta x
That value of c_{i} will be substituted in our function f(x), so we will obtain the following:
f(c_{i}) = (-1 + i \Delta x)^{3} - ( -1 + i \Delta x)
Raising the cube we will obtain the following expression:
f(c_{i}) = \cancel{-1} + 3i\Delta x - 3i^{2}\Delta x^{2} + i^{3} \Delta x^{3} \cancel{+1} - i\Delta x
Thus, the value of f (c_ {i}) is:
=i^{3} \Delta x^{3} - 3i^{2} \Delta x^{2} + 2i \Delta x
Let’s go with the substitution
Let’s replace the f(c_{i}) and the \Delta x that come out in the area function of the limit of the Riemann summation:
\displaystyle A = \underset{n \to \infty} \lim \; \sum_{i = 1}^{n} f(c_{i})\Delta x
\displaystyle =\underset{n\to\infty}\lim\; \sum_{i=1}^{n}(i^{3} \Delta x^{3} - 3i^{2} \Delta x^{2} + 2i\Delta x)\cfrac{3}{n}
Applying properties of the summation, we can write the following:
\displaystyle \underset{n \to \infty} \lim \; \cfrac{3}{n}\left[ \Delta x^{3} \sum_{i=1}^{n} i^{3} - 3\Delta x^{2} \sum_{i=1}^{n} i^{2} + 2\Delta x\sum_{i = 1}^{n}i \right]
We only need to make those summations, to make so many operations faster, in properties of the summation you will find the additions already made, just replace:
\underset{n\to \infty}\lim\; \cfrac{3}{n} \left[ \Delta x^{3} \cfrac{(n^{2}(n+1)^{2})}{4} - 3\Delta x^{2}\cfrac{(n(n+1)(2n+1))}{6} + 2\Delta x \cfrac{n(n+1)}{2}\right]
Now those \Delta x can be substituted with the \frac{3}{n} to get the following:
=\underset{n\to\infty}\lim\; \cfrac{3}{n} \left[ \left( \cfrac{27}{n^{3}}\right) \cfrac{(n^{4} + 2n^{3} + n^{2})}{4} - 3\left( \cfrac{9}{n^{2}}\right) \cfrac{(2n^{3} + 3n^{2} + n)}{6} +\cancel{2} \left( \cfrac{3}{\cancel{n}} \cfrac{(n^{\cancel{2}} + \cancel{n})}{\cancel{2}}\right) \right]
By performing the operations inside the brackets, we will obtain the following:
=\underset{n\to\infty}\lim\; \cfrac{3}{n} \left[ \cfrac{27n}{4} + \cancel{\cfrac{27}{2}} + \cfrac{27}{4n} - 9n - \cancel{\cfrac{27}{2}} - \cfrac{9}{2n} + 3n + 3 \right]
Now we will apply limits:
=\underset{n\to\infty}\lim\; \cfrac{81}{4} + \cancel{\cfrac{81}{4n^{2}}} - 27 - {\cfrac{3}{2n^{2}}} + 9 + \cancel{\cfrac{9}{n}}
= \cfrac{81}{4} - 27 + 9
Simplifying we will obtain as a result:
A = \cfrac{9}{4}u^{2}
Checking with the integral and with the limit of the sum of Riemann, we affirm that our result of \frac{9}{4} is correct!
Thank you for being at this moment with us : )