Let’s start first with the formula of the arc length and then we will see a simple exercise.
Arc length formula
\displaystyle L = \int_{a}^{b}\sqrt{1 + \left[ f'(x)\right]^{2}} \ dx
Now that we have the powerful formula to calculate the arc length, let’s go with an example.
Example of arc length
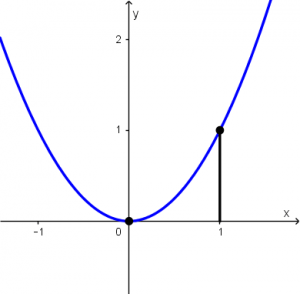
Calculate the arc length of y=x^{2} from x=0 to x=1.
The derivative of f(x)=x^{2} is f'(x) = 2x, so let’s substitute the derivative and the limits in the arc length formula.
\displaystyle L = \int_{0}^{1}\sqrt{1 + \left[ 2x \right]^{2}} \ dx
\displaystyle L = \int_{0}^{1}\sqrt{1 + 4x^{2}} \ dx
In order to solve this exercise we will use trigonometry, we will help us with the following triangle:
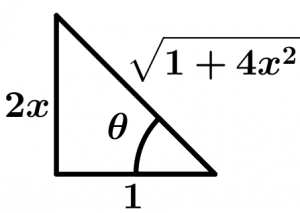 With which we propose the following equations to be able to leave the integral in trigonometric terms:
With which we propose the following equations to be able to leave the integral in trigonometric terms:
\tan \theta = 2x
\sec \theta = \sqrt{1 + 4x^{2}}
We derive \tan \theta to obtain:
\sec^{2}\theta \ d \theta = 2 \ dx
Now we clear the 2 to leave the dx alone:
\cfrac{\sec^{2} \theta}{2} \ d \theta = dx
Once we have the previous equations, substitute in the integral of the arc length of our exercise:
\displaystyle L = \int_{0}^{1} \sqrt{1 + 4x^{2}} \ dx \Rightarrow
\displaystyle L = \int_{0}^{1} \sec \theta \ \cfrac{\sec^{2} \theta}{2} \ d\theta
We will multiply the secants to obtain a secant cube and by properties of the integrals we can extract the 2 from the denominator:
\displaystyle L = \cfrac{1}{2} \int_{0}^{1}\sec^{3} \theta \ d \theta
Consulting the integral of secant cubed, we will obtain the following:
= \left. \cfrac{1}{4}\sec \theta \tan \theta + \cfrac{1}{4} \ln \left| \sec \theta + \tan \theta \right| \right]_{0}^{1}
Now, substituting back the values of x, remember that \tan \theta = 2x and \sec \theta = \sqrt{1+ 4x^{2}}, we get:
= \cfrac{1}{4} \left[ 2x \sqrt{1 + 4x^{2}} + \ln \left| \sqrt{1 + 4x^{2}} + 2x\right|\right]_{0}^{1}
Evaluating the limits we will obtain:
= \cfrac{1}{4} \left[\left( 2\sqrt{5} + \ln\left| 2 + \sqrt{5}\right|\right) - \left(0 \right) \right]
Finally we obtain a result of:
L = \cfrac{2\sqrt{5} + \ln\left| 2 + \sqrt{5}\right|}{4}
So our arc length is:
L = \cfrac{2\sqrt{5} + \ln\left| 2 + \sqrt{5}\right|}{4}\approx 1.48 \ \text{u}
The \text{u} means units.
Thank you for being at this moment with us : )