Formula to find the arc length
\displaystyle S = \int_{\alpha}^{\beta}\sqrt{\left( \cfrac{d\rho}{d\theta}\right)^{2} + \rho^{2}} \ d \theta
Example. Let’s calculate the arc length of a cardioid
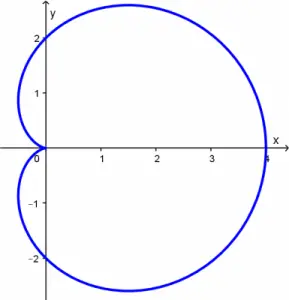
The cardioid to which we are going to find its arc length is \rho = 2 (1 + \cos \theta), graphically it looks like this:
\rho = 2(1 + \cos \theta)
As it says in the formula, we need to calculate the derivative of \rho. To do so, let’s multiply the 2 with the parenthesis:
\rho = 2 + 2 \cos \theta
And now we proceed to derive, derivative of a constant is equal to zero and derivative of cosine is equal to -\sin:
\rho ' = 0 - 2\sin \theta
\rho ' = -2 \sin \theta
What you have to do is substitute in the integral the values of the derivative and the square of \rho:
\displaystyle S = \int_{\alpha}^{\beta}\sqrt{(-2\sin \theta)^{2} + (2(1 + \cos \theta))^{2}} \ d\theta
And what are our limits of angles in radians of \alpha and \beta?
There are two options to place the limits in the integral. The first option is to place the limits from zero to \pi, that the result will only give us half the value of the full length, which means that you have to multiply the result by 2.
The second option is to place the limits from zero to 2\pi, which represents that you will give once and for all the return to the cardioid. With the two options you reach the same result, let’s continue:
We will put a 2 to the integral because we are going to integrate from zero to \pi and we squared to obtain:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{4\sin^{2}\theta + 4(1 + 2 \cos \theta + \cos^{2} \theta)} \ d\theta
Multiply the parenthesis where the 4 is:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{4\sin^{2} \theta + 4 + 8 \cos \theta + 4 \cos^{2} \theta} \ d \theta
We are going to order the term 4\sin^{2}\theta and the term 4\cos^{2}\theta and we will factor the 4:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{4(\sin^{2}\theta + \cos^{2} \theta) + 4 + 8 \cos \theta} \ d \theta
Remember a very powerful trigonometric identity:
\sin^{2}\theta + \cos^{2}\theta = 1
With the trigonometric identity, let’s reduce terms:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{4 + 4 + 8\cos \theta} \ d \theta
Let’s sum the 4‘s:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{8 + 8\cos \theta} \ d \theta
Let’s factorize 8:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{8(1 + \cos \theta)} \ d \theta
And that 8 we can represent it as 2^{2}\cdot 2:
\displaystyle S = 2 \int_{0}^{\pi}\sqrt{2^{2}\cdot 2(1 + \cos \theta)} \ d \theta
That 2^{2}\cdot 2 can be taken from the square root and then, by integral properties, remove it from the integral:
\displaystyle S = 2 \int_{0}^{\pi} \left(2\sqrt{2} \right) \sqrt{1 + \cos \theta} \ d \theta
\displaystyle S = 2\left( 2\sqrt{2}\right)\int_{0}^{\pi}\sqrt{1 + \cos \theta} \ d\theta
Multiply terms:
\displaystyle S = 4\sqrt{2}\int_{0}^{\pi}\sqrt{1 + \cos \theta} \ d \theta
Well, and how is it integrated?
Relax, that is easily integrated using the following trigonometric identity:
\cos^{2}\left(\cfrac{\theta}{2}\right) = \cfrac{1+\cos \theta}{2}
That trigonometric identity we will apply to it a square root to obtain:
\cos \left( \cfrac{\theta}{2}\right) = \cfrac{\sqrt{1 + \cos \theta}}{\sqrt{2}}
Now to the integral to which we arrived, we are going to multiply and divide a \sqrt{2} to be equal to the trigonometric identity:
\displaystyle S = 4\sqrt{2} \int_{0}^{\pi} \sqrt{2}\cfrac{\sqrt{1 + \cos \theta}}{\sqrt{2}} \ d \theta
By properties of integrals, we will extract the \sqrt{2} from the integral that is found as a numerator:
\displaystyle S = 4 \sqrt{2}\cdot\sqrt{2}\int_{0}^{\pi}\cfrac{\sqrt{1 + \cos \theta}}{\sqrt{2}} \ d \theta
Now our integral is similar to what we did in the trigonometric identity! Just replace what is in the integral by \cos\left(\frac{\theta}{2}\right) and multiply the two square roots of 2 and the 4:
\displaystyle S = 8\int_{0}^{\pi}\cos \left( \cfrac{\theta}{2} \right) \ d \theta
To solve that integral, we will replace u to \frac{\theta}{2}, we will derive and clear:
u = \cfrac{\theta}{2}
du = \cfrac{d\theta}{2}
2 \ du = d \theta
Let’s substitute those terms in the integral:
\displaystyle S = 8 \int_{0}^{\pi} \cos (u ) (2 \ du)
Let’s apply properties of integrals to take the 2 and multiply it with the 8:
\displaystyle S = 16 \int_{0}^{\pi}\cos(u) \ du
Remember that the integral of cosine is equal to sine, so let’s integrate:
S = 16 \left. \sin(u)\right|_{0}^{\pi}
Let’s return the \frac{\theta}{2}:
S = 16 \left. \sin\left( \cfrac{\theta}{2} \right) \right|_{0}^{\pi}
Using a calculator in radians, let’s evaluate the sine:
S = 16 \left( 1 -0\right)
And finally our result of the cardioid arch length is:
S = 16 \ \text{u}
The \text{u} of the final result means “units”, that is, the length is 16 units.
Thank you for being at this moment with us : )