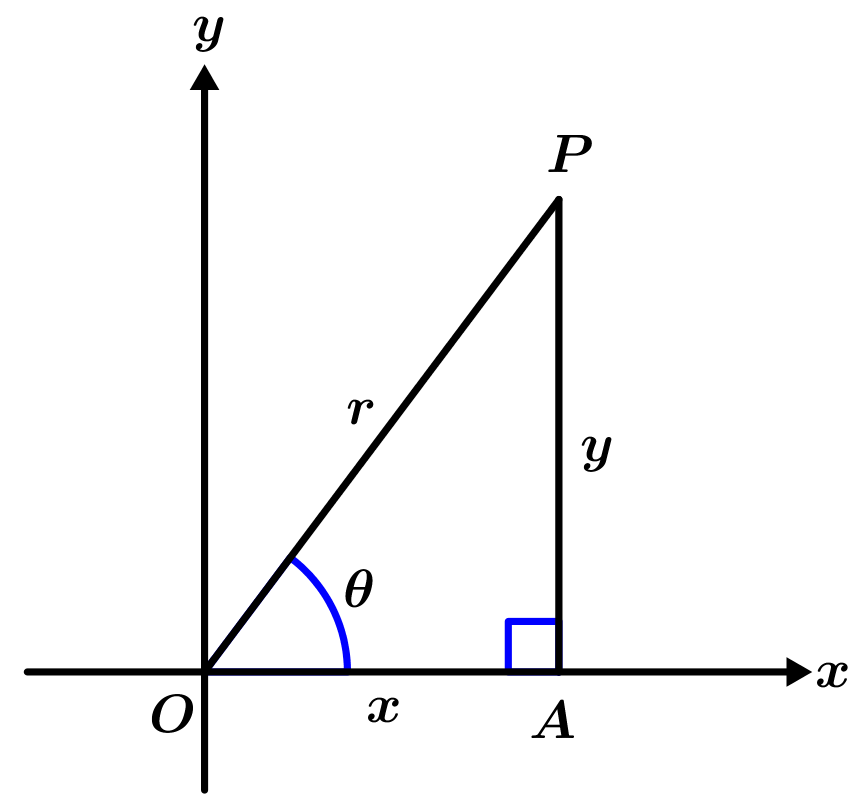
The polar representation of a complex number is also known as the trigonometric form of a complex number, next we will see the polar representation of P which is the complex number x + yi:
In the triangle observed in Figure 1, you can write the following:
x = r \cos \theta, \qquad y = r \sin \theta
r = \sqrt{x^{2} + y^{2}}, \qquad r \ge 0
\tan \theta = \cfrac{y}{x}, \qquad x \neq 0
With the data mentioned, we can write that:
x + yi = r \cos \theta + i \sin \theta = r\left( \cos \theta + i \sin \theta \right)
The member r\left(\cos \theta+i\sin \theta \right) is what is known as the polar form of the complex number x+yi.
Note: Remember that the term of the reals is part of the x axis and the imaginary term is part of the y axis.
Module of a complex number
The letter r that we have in the polar equation of the complex number is what is known as the complex number module. This r module is also called the absolute value of the complex number and can be written as r=\left|x + yi \right|
Argument of a complex number
The angle \theta is known as the amplitude or argument of the complex number and \theta will be restricted to the domain of 0\le \theta \le 360^{\text{o}} unless otherwise specified in some exercise.
Example of complex number to polar form
We are going to transform a complex number of rectangular form into polar form, to do that we have to find the module and the argument, also, it is better to represent the examples graphically so that it is clearer, let’s see the example, let’s start.
Let’s go with the example
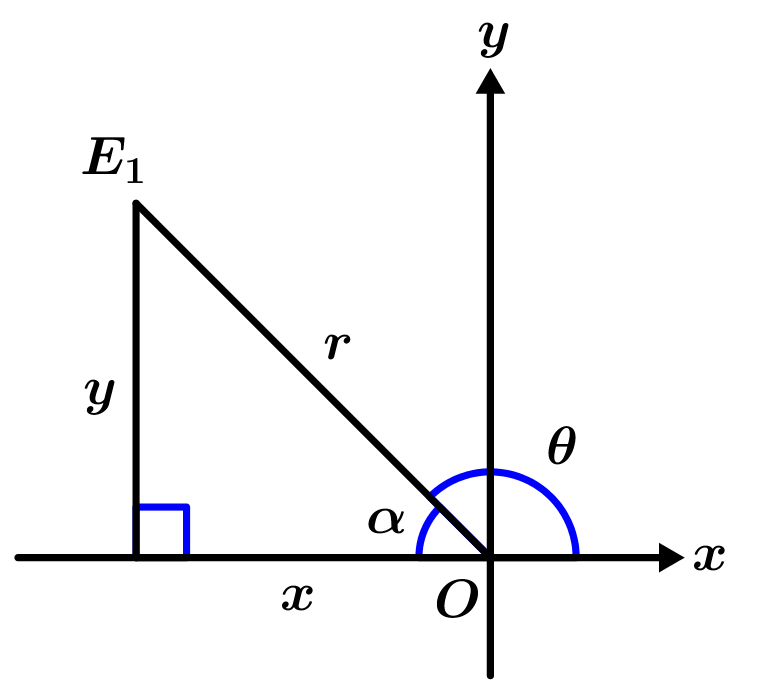
Find the polar form of E_{1} =-2 + 2i
We always try to graph our complex number so that it is easier to interpret the data we want to find.
Let’s find the module in the following way:
x = -2 \qquad y = 2
r = \sqrt{x^{2} + y^{2}} = \sqrt{(-2)^{2} + (2)^{2}} = \sqrt{4 + 4} = \sqrt{8}
r = 2\sqrt{2}
Once we have the module, we must calculate the argument, here we will do a little trick where \alpha represents the angle of elevation of the module, for that we proceed to do the following:
\tan \alpha = \cfrac{y}{x} = \cfrac{2}{-2} = -1
Now you have to apply an inverse tangent to -1, you can use a calculator if you want:
\alpha = \tan^{-1}(-1) = -45^{\text{o}}
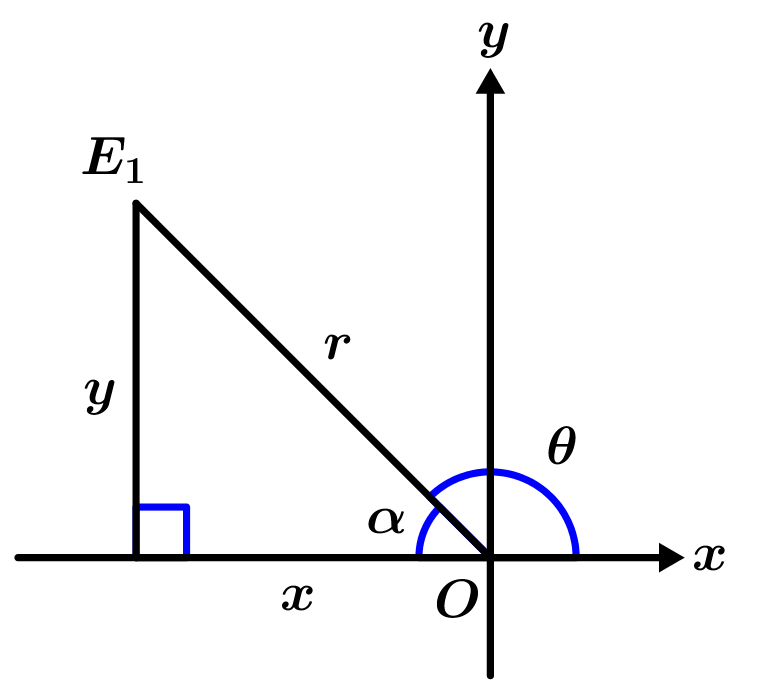
But just calculating the angle is not enough, what we do is ignore the sign that has the calculated angle and we will only take the angle of elevation \alpha in the quadrant where our imaginary number is, in this example, the point E_{1} tells us that we are in the second quadrant, so the elevation angle of the module line r measures 45°, the angle \theta is measured from the positive line of the abscissa to the line of the module, observing Figure 3 you can see where \theta is located.
So \theta=180°-\alpha=135°
Once the module and the argument of the complex number have been calculated, finally we have that the polar form of -2+2i is:
2\sqrt{2} \left( \cos 135°+ i \sin 135° \right)
How do we verify that the polar form of a complex number found is correct?
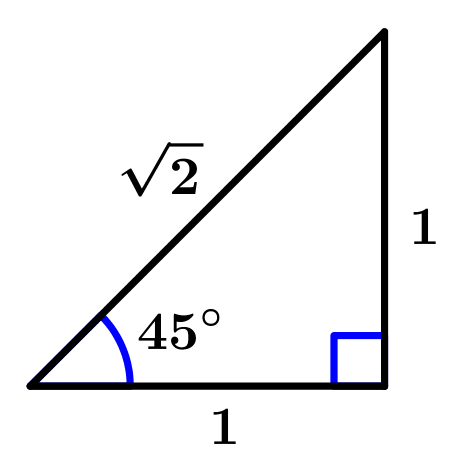
I’ll be honest, the truth is that it’s quite simple to check if our polar form of the imaginary number is correct, for this case you only need a right triangle like the one in figure 4.
That triangle is for illustrative purposes only, adjustments will be made in the march.
If you do not have a calculator (imagine that at the moment you saved it and do not want to go for it) to calculate the value of \cos 135°, you can perform the calculation of -\cos 45° since they give exactly the same result, the negative sign is added because the angle is in the second quadrant and as cosine makes representation to x (the real numbers ), if it is in the second or third quadrant, it will take negative values. With practice you will realize that you can work in the first quadrant for the ease of positive signs, but you must remember that you always have to place the signs depending on the quadrant where the original angle belongs. Well, let’s continue, cosine is adjacent leg divided by the hypotenuse:
-\cos 45° = -\cfrac{1}{\sqrt{2}} = - \cfrac{\sqrt{2}}{2}
Great, once we have the value of \cos 135°, we will find the value of \sin 135°. Working with our triangle of Figure 4, \sin 135° is equal to \sin 45°, and as the sine is opposite led divided by the hypotenuse, we will have the following:
\sin 45° = \cfrac{1}{\sqrt{2}} = \cfrac{\sqrt{2}}{2}
Once we have the two values of \cos 135° and \sin 135°, we will replace them in our polar form:
2\sqrt{2} \left( \cos 135° + i \sin 135°\right) = 2\sqrt{2} \left( -\cfrac{\sqrt{2}}{2} + i\cfrac{\sqrt{2}}{2} \right)
We multiply the parentheses to obtain the following:
2\sqrt{2} \left( -\cfrac{\sqrt{2}}{2} \right) + 2\sqrt{2}\left(\cfrac{\sqrt{2}}{2} \right)i
By carrying out the corresponding operations, we will have:
-\sqrt{2}\sqrt{2} + i\sqrt{2}\sqrt{2} = -2 + 2i
As the result gave us our complex number that gives us the exercise, then the complex number -2+2i in the polar form 2\sqrt{2}\left (\cos 135° + i\sin 135° \right) is correct!
Thank you for being at this moment with us:)
I highly recommend the following algebra book:
