A continuación veremos una de las distribuciones más presentes en la probabilidad, que es la distribución hipergeométrica, la cual explicaremos a continuación.
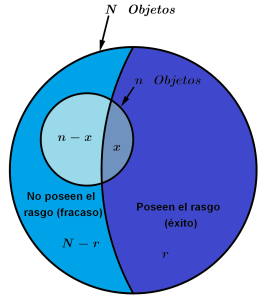
Esta distribución consiste en extraer una muestra aleatoria de tamaño n sin reemplazo ni consideración de su orden, de un conjunto de N objetos.
Es decir que los eventos son dependientes y de los N objetos, r poseen el rasgo que nos interesa, además, la variable aleatoria X es el número de objetos de la muestra que poseen dicho rasgo.
Así que para tener esto más claro, existen combinaciones N \choose n formas igualmente probables de seleccionar n objetos, dando así que para lograr x éxitos, se deben seleccionar x objetos de entre los r que tienen el rasgo que nos interesa, habiendo r \choose x maneras y además deben seleccionarse los n - x objetos de los N - r objetos que no tienen el rasgo, habiendo combinaciones {N-r} \choose{n-x}.
Fórmulas de la distribución hipergeométrica
Usando la fórmula clásica de probabilidad y la regla de multiplicación, la densidad de probabilidad se obtiene de la siguiente manera:
P[X = x] = \cfrac{ {r\choose x} {N-r \choose n-x} }{N \choose n }\quad \text{max}[0,n-\left(N-r\right) \le x \le \ \text{min}\left(n,r\right)]
Sus características más importantes son las que se muestran a continuación de la esperanza y la varianza
E[X] = n \left( \cfrac{r}{N} \right)
Var[X] = n \left( \cfrac{r}{N} \right) \left( \cfrac{N - r}{N} \right) \left( \cfrac{N-n}{N-1} \right)
El significado de las incógnitas de las fórmulas anteriores son los siguientes:
- N es nuestra población por lote
- r que son nuestras unidades defectuosas por lote
- n que es el número de unidades que se prueban
- x es lo esperado, para calcular la probabilidad de que x cantidades tengan alguna condición
Ejemplo de distribución hipergeométrica
Una fundidora embarca bloques en lotes de 20 unidades. Ningún proceso de manufactura es perfecto, de modo que los bloques defectuosos son inevitables. Sin embargo, es necesario destruirlos para identificar el defecto. Se seleccionan y prueban tres unidades antes de aceptar un lote. Suponga que un lote dado incluye cinco unidades defectuosas.
a) Exprese la función de densidad.
Para este ejercicio tenemos nuestros siguientes datos:
- N son 20 unidades
- r son 5 unidades defectuosas
- n son 3 unidades que se prueban
Con estos datos podemos proceder a escribir nuestra fórmula de la densidad:
P[X = x] = f(x) = \cfrac{ {r\choose x} {N-r \choose n-x} }{N \choose n } = \cfrac{ {5\choose x} {20-5 \choose 3-x} }{20 \choose 3 } \quad x = 0,1,2,3
Así que ahora tenemos que calcular cada una de las probabilidades con los valores de x, que es la probabilidad de que ninguna, una, dos o tres sean defectuosas:
x= 0 \qquad f(x) = \cfrac{ {5\choose 0} {15 \choose 3-0} }{20 \choose 3 } = \cfrac{91}{228}\approx 0.399
Así que existe un 39.9% de que cero unidades salgan defectuosas.
x= 1 \qquad f(x) = \cfrac{ {5\choose 1} {15 \choose 3-1} }{20 \choose 3 } = \cfrac{35}{76}\approx 0.46
Existe un 46% de probabilidad de que una unidad salga defectuosa.
x= 2 \qquad f(x) = \cfrac{ {5\choose 2} {15 \choose 3-2} }{20 \choose 3 } = \cfrac{5}{38}\approx 0.131
Existe un 13.1% de probabilidad de que dos unidades salgan defectuosas.
x= 3 \qquad f(x) = \cfrac{ {5\choose 3} {15 \choose 3-3} }{20 \choose 3 } = \cfrac{1}{114}\approx 0.008
Existe un 0.8% de probabilidad de que tres unidades salgan defectuosas.
b) Halla el valor esperado de unidades defectuosas
Para hallar este valor aplicaremos la fórmula de la esperanza:
E(X) = n\left( \cfrac{r}{N}\right) = 3\left(\cfrac{5}{20} \right) = \cfrac{3}{4} = 0.75
Así que nuestra esperanza de obtener unidades defectuosas es de 0.75 o un 75%
c) Encuentra la varianza para este caso
Y para hallar el valor de la varianza también aplicaremos la pura fórmula:
Var(X)=n\left(\cfrac{r}{N}\right)\left(\cfrac{N-r}{N}\right)\left(\cfrac{N-n}{N-1}\right)
=3\left(\cfrac{5}{20}\right)\left(\cfrac{20-5}{20}\right)\left(\cfrac{20-3}{20-1}\right)
3\left(\cfrac{5}{20}\right)\left(\cfrac{15}{20}\right)\left(\cfrac{17}{19}\right) = \cfrac{153}{304}
Lo que nos da un valor aproximado de la varianza de 0.5032
Eso es todo, esperamos se haya entendido lo mejor posible la distribución hipergeométrica.
Gracias por estar en este momento con nosotros : )
