Funciones – ¡Explicación completa y ejemplos! 📈

Ha llegado el momento de encontrarnos con un nombre con el cual se toparán muchas veces aquellos que estudian alguna ingeniería (aun que igual se utiliza en otros campos de estudio), y es el nombre de función o funciones.

Qué es una función

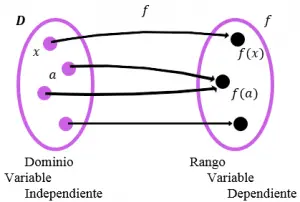
Una función f es una regla de correspondencia que asocia a cada objeto x en un conjunto – denominado dominio – un sólo valor f(x) de un segundo conjunto. El conjunto de todos los valores así obtenidos se llama rango.

\{ x,f(x) | x \in D\}

Para denotar una función se utiliza una letra fuera del paréntesis y algo que esté dentro del paréntesis f(x), donde lo que está adentro del paréntesis significa el valor que tomará cada variable. Mira cómo se afecta la función f(x) cuando asignamos los siguientes valores de f(1), f(a) y f(a + h):

\Rightarrow f(x) = x^{2} + 2 \qquad
\begin{array}{l}
f(1) = 1^{1} + 2 = 3 \\
f(a) = a^{2} + 2 \\
f(a + h) = (a + h)^{2}+2 = a^{2} + 2ah + h^{2} + 2
\end{array}

El dominio de una función

• El dominio de la función es un conjunto de valores permitidos para una función
• Si no se especifica, se supone que son todos los reales (\mathbb{R}), de todas maneras se tiene que analizar el dominio de la función porque no siempre son todos los reales
• Se deben excluir del dominio aquellos números que causen una división entre cero o raíz cuadrada de un número negativo

Ejemplos de dominios de las funciones

(a) f(x) = x + 2

El dominio de la función son todos los reales, \mathbb{R}

D: \ \mathbb{R}

(b) f(x) = \sqrt{x - 8}

El dominio de esta función son todos los valores que hagan que el resultado dentro de la raíz cuadrada sea mayor o igual a cero. Como lo que se quiere es que el dominio sea mayor o igual a cero, se toma la expresión dentro de la raíz cuadrada y se resuelve una desigualdad:

x - 8 \ge 0 \ \rightarrow \ x \ge 8

D: \ x \ge 8

Así que el dominio de la función es todo valor mayor o igual a 8.

(c) f(x) = \cfrac{2}{x + 4}

El dominio de la función son todos los valores que hagan que el resultado del denominador de la fracción sea diferente de cero. Por lo tanto, el dominio de la fracción son todos los reales, excepto el -4:

x + 4 \neq 0 \longrightarrow x \neq -4

D: \ \mathbb{R} - \{-4\}

(d) f(x) = \cfrac{x}{x^{2} - 9}

Como en el ejercicio anterior, el resultado del denominador de la fracción tiene que ser diferente de cero, vamos a calcularlo:

x^{2} - 9 \neq 0 \rightarrow x \neq \pm 3

D: \ \mathbb{R} - \{3,-3\}

(e) f(x) = \cfrac{1}{\sqrt{4 - x^{2}}}

Como lo que se quiere es evitar que el resultado del denominador de la fracción sea cero y que el resultado de la raíz cuadrada sea un número negativo, se tiene que hacer lo siguiente:

4 - x^{2} > 0

Factorizamos

(2 - x)(2 + x) > 0

Y obtendremos el resultado del dominio de nuestra función:

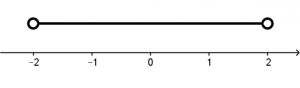
D: (-2,2)

D: -2 < x < 2

(f) f(x) = \sqrt{49 - x^{2}}

Se necesita que el resultado dentro de la raíz dé números mayores o iguales a cero, por lo que se tiene lo siguiente:

49 - x^{2} \ge 0

Ahora factorizamos

(7 - x)(7 + x) \ge 0

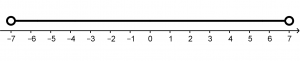
Y gráficamente el dominio de nuestra función se vería de la siguiente manera

D: [-7,7]

D:\ -7\le x \le 7

Maneras de representar a una función

Hay 4 maneras de representar a una función

1. Verbalmente

Función equis cuadrada; función seno; función raíz cuadrada de x; etc. etc.

2. Numéricamente

Tabulando la función valor por valor

\begin{array}{c | c}  x & y \\ \hline \\ \\ \\ \end{array}

3. Visualmente

4. Algebráicamente

f(x) = x + 1

Rango de las funciones

El rango será definido por la regla de correspondencia (consiste en asignar un elemento único de un cierto conjunto a cada elemento único de otro conjunto) y el dominio.

Quiere decir que el rango son los valores que puede tomar en el eje y. Por ejemplo:

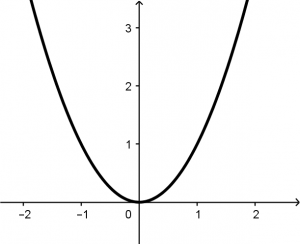
La parábola y= x^{2} tiene de dominio a todos los números reales: D:\ \mathbb{R} y de rango sólo tiene valores de cero hasta infinito porque son los valores que tomará y con la función de nuestra parábola y = x^{2}

y = x^{2}

Cuáles curvas en el plano xy son gráficas de funciones

Prueba de la línea vertical

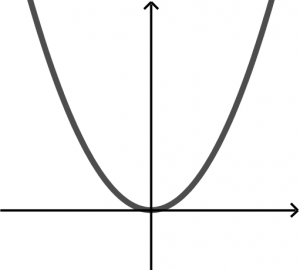
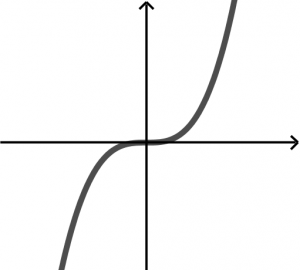
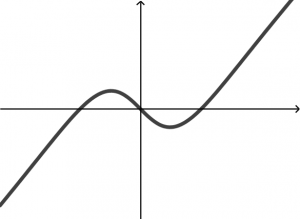
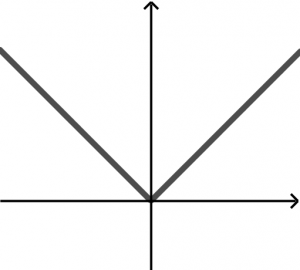
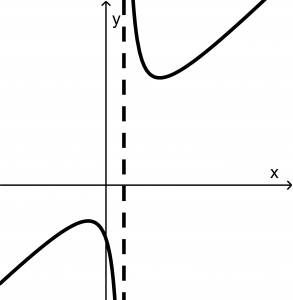
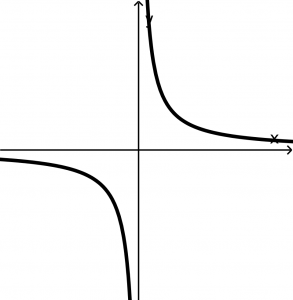
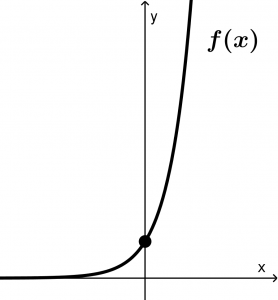
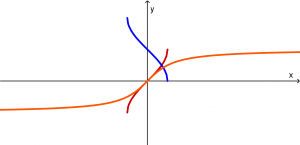
Una curva en el plano xy es gráfica de una función de x si ninguna línea vertical interseca con la curva más de una vez. Imagina que a las siguientes gráficas las atravesamos con una línea vertical:

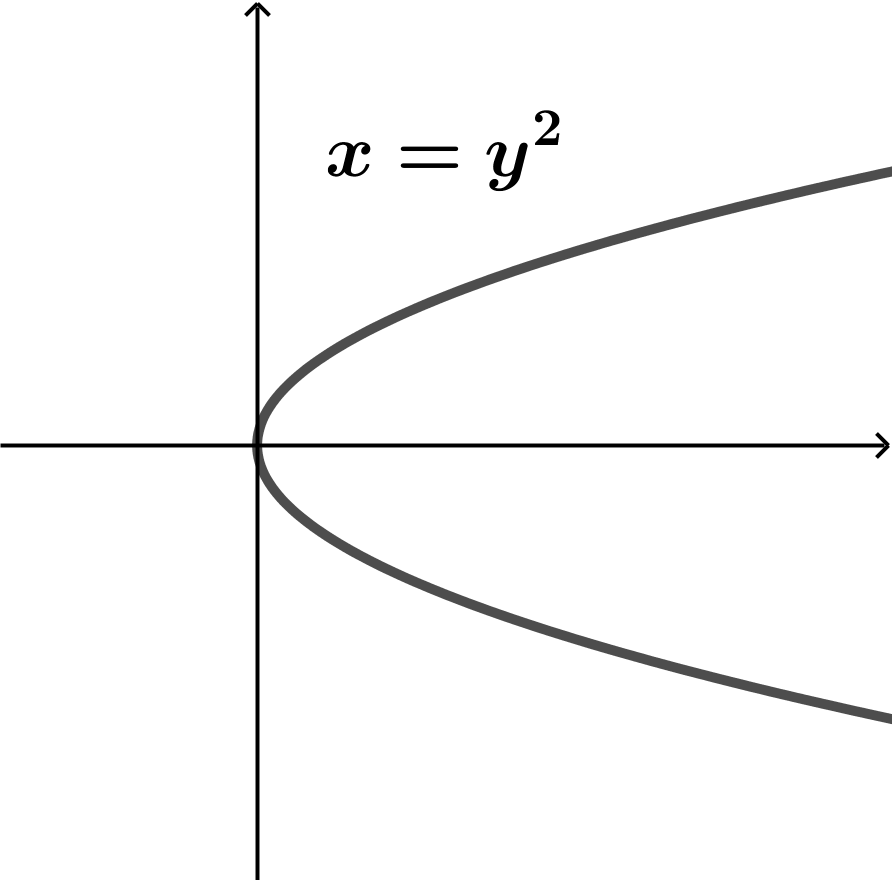
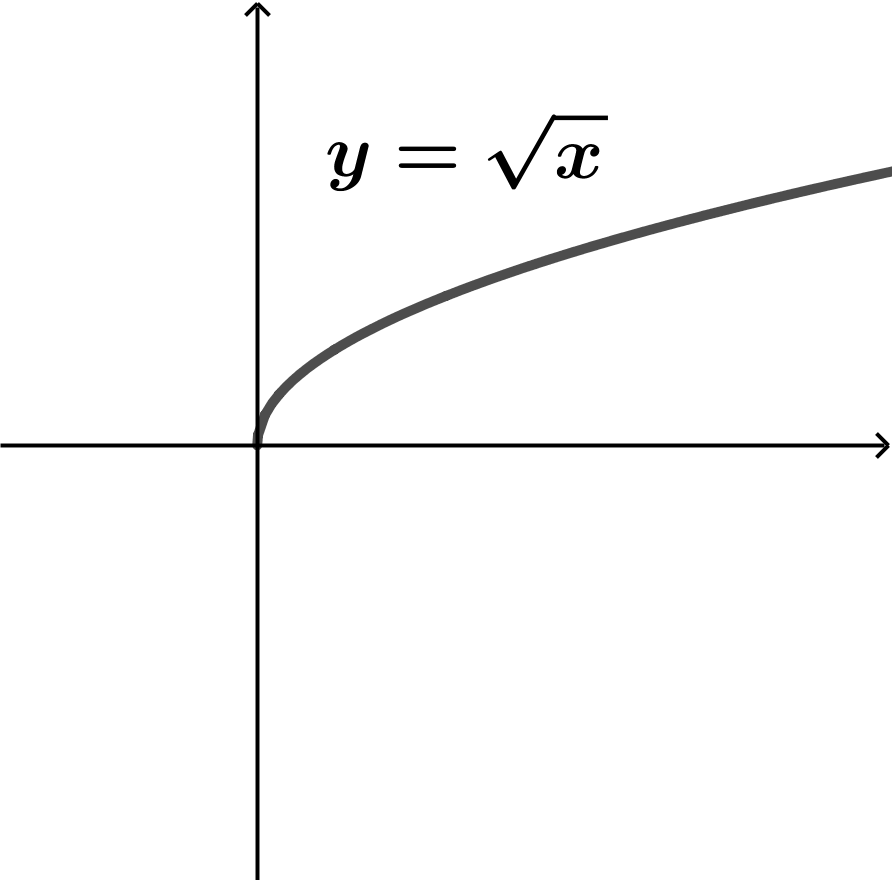
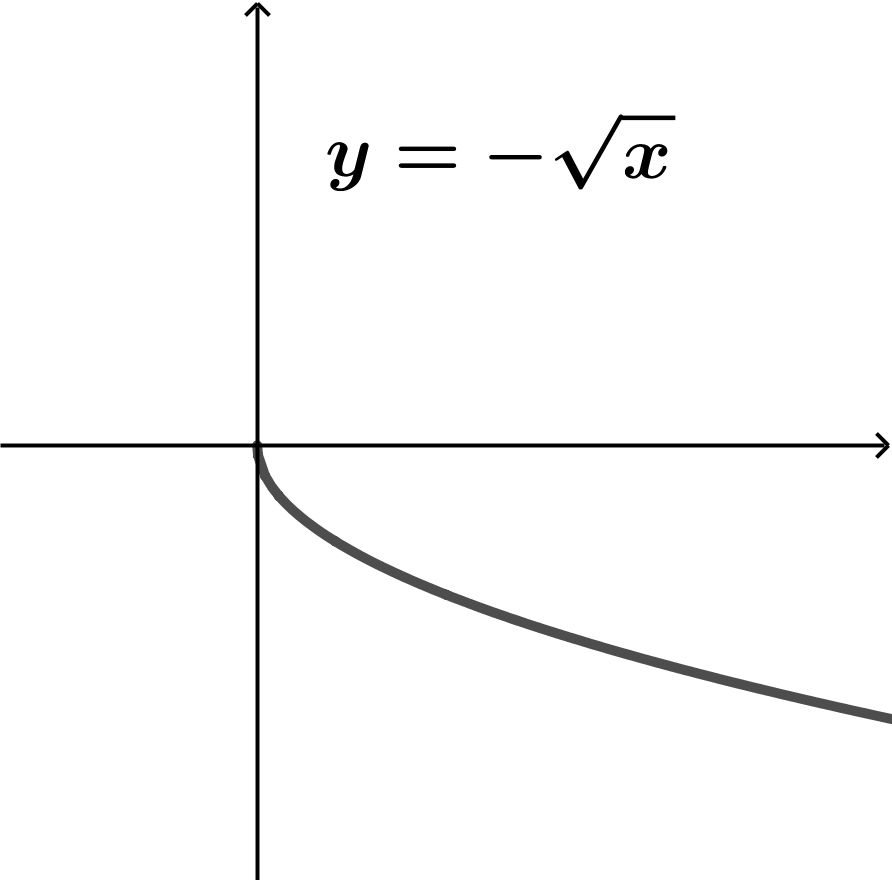
La primera no es gráfica de una función porque si imaginamos que es atravesada por una línea vertical, cortará a la gráfica en dos puntos.

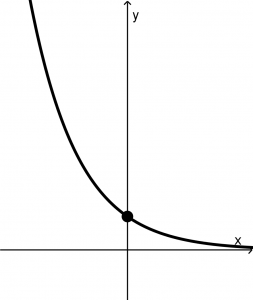
La segundo gráfica y la tercera gráfica sí son resultados de funciones porque la línea vertical imaginaria no atraviesa más de una vez a las gráficas.

Simetría de las funciones

• Una función f(x) es una función par si para cada xdel dominio de f se cumple: f(-x) = f(x). Este quiere decir que es par si la función es simétrica con respecto al eje y.
• Una función f(x) es una función impar si para cada x del dominio de f se cumple: f(-x) = -f(x). Quiere decir que es impar si la función es simétrica con respecto al origen.

Ejemplos:

(a) f(x) = x^{2}

f(-x) = (-x)^{2} = x^{2} \quad \text{PAR}

f(x) = x^{2}

(b) f(x) = x^{3}

f(-x) = (-x)^{3} = -x^{3}\quad \text{IMPAR}

f(x) = x^{3}

(c) h(x) = 2x^{4} + 7x^{3} - x^{2} + 9

h(-x) = 2x^{4} - 7x^{3} - x^{2} + 9 \quad \text{NO es PAR ni IMPAR}

(d) f(x) = \cfrac{x^{3} -x}{x^{2} + 1}

f(-x) = \cfrac{-x^{3} + x}{x^{2} + 1} = - \left ( \cfrac{x^{3} - x}{x^{2} + 1} \right ) \quad \text{IMPAR}

f(x) = \cfrac{x^{3} -x}{x^{2} + 1}

(e) f(x) = |x|

f(x) =
\begin{cases}
x & x \ge 0 \\
-x & x < 0
\end{cases}

\text{PAR}

f(x) = |x|

Clasificación de las funciones

Función inyectiva

A cada valor del dominio le corresponde un valor del rango (igual llamado contradominio). Significa que no hay dos o más elementos que tengan la misma imagen.

Igualmente se le conocen como funciones uno a uno.

y=x^{3} es una función uno a uno

y  =x^{2} no es función uno a uno

Función suprayectiva (función sobreyectiva)

A cada elemento del rango le corresponde al menos uno del dominio

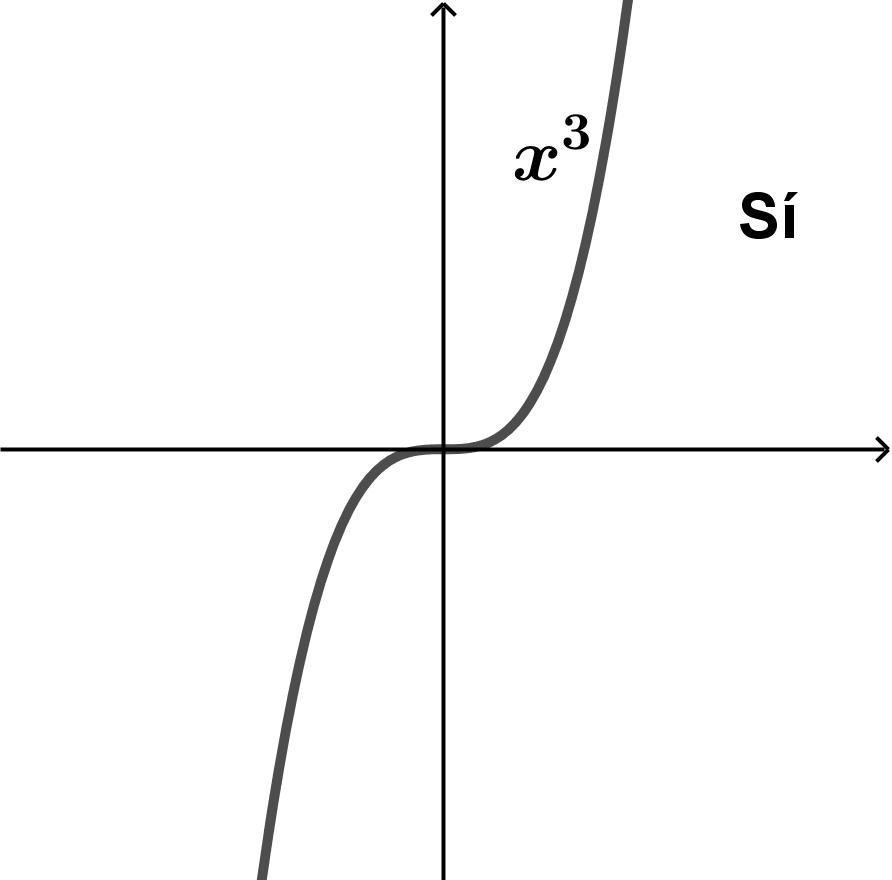
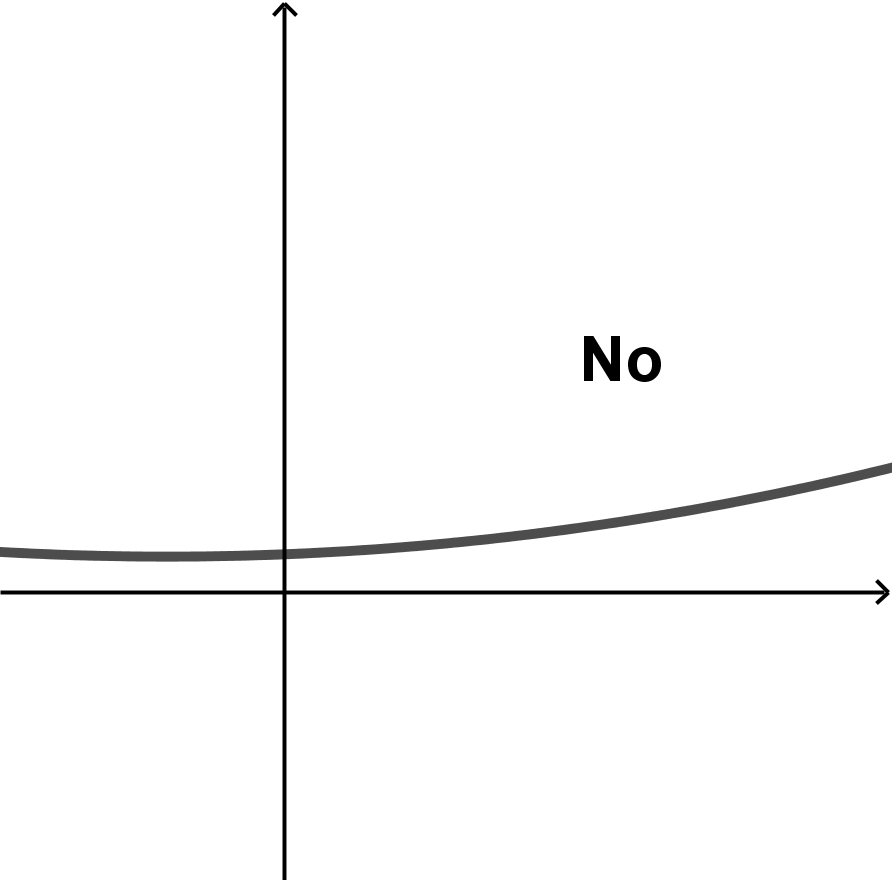
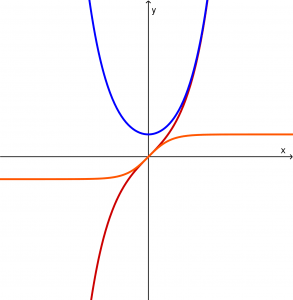
La primera gráfica es suprayectiva porque a cada valor de y le corresponde un valor de x. Ya que a todo el rango le corresponde un valor del dominio.

La segunda gráfica no es sobreyectiva porque hay elementos del rango (valores negativos de y) en los cuales no está incluida la gráfica.

Función biyectiva

Es una función que es inyectiva y sobreyectiva, ejemplos:

• f(x) = 5x - 3
• f(x) = x^{3}

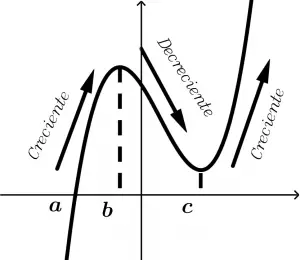
Monotonía de una función: Crecientes y decrecientes

Se dice que una función es creciente sobre un intervalo I si:

f(x_{1}) < f(x_2) \ \text{siempre que} \ x_{1} < x_{2} \ \text{en} \ I

Se dice que f(x) es una función decreciente sobre I si:

f(x_{1}) > f(x_{2}) \ \text{siempre que} \ x_{1} < x_{2} \ \text{en} \ I

Tipos de funciones

Funciones algebráicas

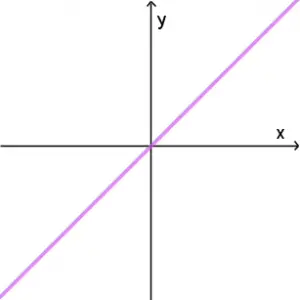
Función identidad

f(x) = x

Función polinomial

f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + \dots + a_{1} x + a_{0}

f(x) = 5x^{7} + 7x^{4} - 3x^{2} + 2 \quad \text{}

f(x) = x^{2} + 3 \quad \text{cuadrática}

f(x) = 5x^{3} - x \quad \text{cúbica}

Una función algebráica está formada por un número finito de operadores algebráicos sobre la función identidad y una función constante.

Los operadores algebráicos son: adición, sustracción, multiplicación, división, potenciación, radicación.

Ejemplos de funciones polinomiales

Función racional

f(x) = \cfrac{x^{2} + 3}{x - 1} \quad \Rightarrow \quad f(x) = \cfrac{P(x)}{Q(x)}

f(x) = \cfrac{x^{2} + 3}{x - 1}

Función recíproca

f(x) = \frac{1}{x}

Función radical

f(x) = \sqrt{x + 3}

Funciones trascendentales

Funciones trigonométricas

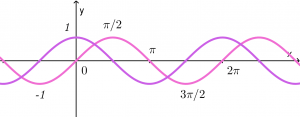
Función seno y función coseno

f(x) = \sin x

g(x) = \cos x

-1 \le \sin x \le 1

-1 \le \cos x \le 1

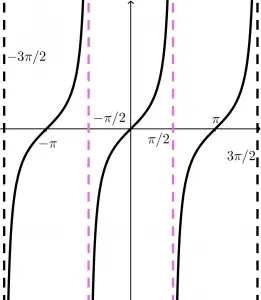
Funciones tangente

f(x) = \tan \ (x) = \cfrac{\sin \ x}{\cos \ x}

Tienen una propiedad interesante que es la de periodicidad

\begin{array}{c}
\sin \ (x + 2 \pi) = \sin \ x \\
\cos \ (x + 2 \pi) = \cos \ x \\
\tan \ (x + \pi) = \tan \ x
\end{array}

Funciones exponenciales

f(x) = a^{x}

x es una variable que está en el exponente

f(x)= 5^{x}

\begin{array}{c c c}
f(x) = 5^{x} & x = 0 & f(0) = 5^{0} = 1 \\
& & f(1) = 5^{1} = 5 \\
& & f(2) = 25 \\
& & f(-10)=5^{-10}=\cfrac{1}{5^{-10}} \sim 0
\end{array}

Recordar:

• Si x = n es entero positivo, entonces a^{x} = a \cdot a \cdot a
• Si x = 0, entonces a^{0} = 1
• Si x = -n, entonces \frac{1}{a^{n}}
• Si x = p / q y q > 0, entonces a^{x} = \sqrt[q]{a^{p}} ó (\sqrt[q]{a})^{p}

Ejemplo:

f(x) = (0\text{.}5)^{x} = \left ( \cfrac{1}{2}\right)^{x} = \cfrac{1}{2^{x}}

f(x) = (0 \text{.}5)^{x}

Funciones logarítmicas

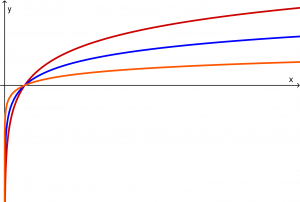
f(x) = \log_{a}x

\log_{2}(x)   \log_{3}(x)   \log_{10}(x)

Donde a es la base de una constante positiva, o sea a > 0

Una propiedad muy importante a considerar de los logaritmos es la siguiente:

f(1) = \log_{a}(1) = 0

Ahora, ¿a qué número se eleva la base para llegar al argumento? Simple, observa:

\log_{a}x = n \ \Rightarrow \ a^{n} = x

Funciones hiperbólicas

\sinh \ (x) = \cfrac{e^{+x} - e^{-x}}{2}

\cosh \ (x) = \cfrac{e^{+x} + e^{-x}}{2}

\tanh \ (x) = \cfrac{\sinh \ (x)}{\cosh \ (x)}

Funciones trigonométricas inversas

\arcsin \ (x)

\arccos \ (x)

\arctan \ (x)

Funciones especiales, también llamadas funciones seccionadas

f(x) = \ \begin{cases} g(x) & x < a \\ h(x) & a \le x \le b \\ k(x) & x > b\end{cases}

Ejemplos de funciones seccionadas

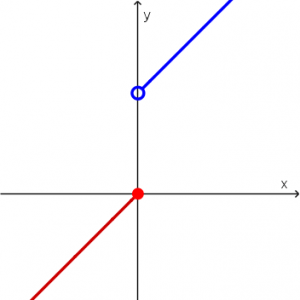
f(x) = \ \begin{cases} x & x \le 0 \\ x + 1 & x > 0\end{cases}

Dominio: \mathbb{R}

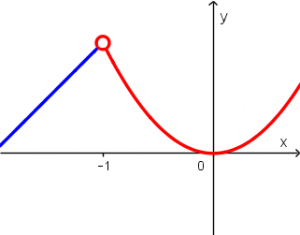
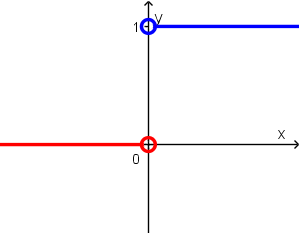
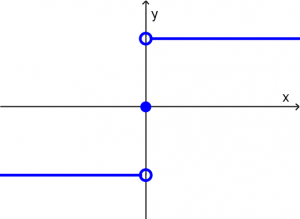
f(x) = \ \begin{cases} x + 2 & x \le -1 \\ x^{2} & x > -1 \end{cases}

Escalón unitario o escalón de Heaviside

H(x) = \ \begin{cases} 0 & x < 0 \\ 1 & x > 0\end{cases}

Función signo

\text{sgn}(x) = \ \begin{cases} 1 & \text{si } x > 0 \\ 0 & \text{si } x = 0 \\ -1 & \text{si } x < 0  \end{cases}

Operaciones con funciones

Se pueden combinar dos funciones para formar nuevas.

Sea f \ \land \ g \quad \Rightarrow \quad puede obtenerse f + g, f - g, f \cdot g, \cfrac{f}{g}

Cada uno con dominios A \ \land \ B

\begin{array}{c c c c c}
& & & & \text{dominio} \\
\Rightarrow & (f + g)(x) & = & f(x) + g(x) & A \cap B \\
& (f - g)(x) & = & f(x) - g(x) & A \cap B \\
& (f \cdot g)(x) & = & f(x) \ \cdot \ g(x) & A \cap B \\
& \bigg ( \cfrac{f}{g} \bigg ) (x) & = & \cfrac{f(x)}{g(x)} & \{ x \in \ A \cap B \ | \ g(x) \neq 0 \}
\end{array}

Ejemplo f(x) = \sqrt{x} \quad g(x) \sqrt{4 - x^{2}}

\sqrt{x} \ D: \ x \ge 0 \ [0, +\infty)

\sqrt{4 - x^{2}} \ D: \ [-2, 2]

D: [0,+\infty) \cap [-2,2] = [0,2]

\begin{array}{l c}
(f + g)(x) = \sqrt{x} + \sqrt{4 - x^{2}} & [0,2] \\
(f - g)(x) = \sqrt{x}- \sqrt{4 - x^{2}} & [0,2] \\
(f \cdot g)(x) = \sqrt{x}\sqrt{4-x^{2}} = \sqrt{4x - x^{3}} & [0,2] \\
\bigg ( \cfrac{f}{g} \bigg )(x) = \cfrac{\sqrt{x}}{\sqrt{4-x^{2}}}& [0,2)
\end{array}

Composición de funciones

Sea y = f(u) \ \land \ u = g(x) \quad \Rightarrow \quad y = f(g(x))

Ejemplo f(u) = \sqrt{u + 1} \qquad u = g(x) = x^{2} - 1

\Rightarrow Dadas dos funciones f y g la función compuesta está definida por:

(f \circ g)(x) = f(g(x))

Ejemplo de funciones compuestas

Si f(x) \sqrt{x} \qquad g(x) = \sqrt{2 - x}

f \circ g \ \Rightarrow \ f(g(x)) = \sqrt{\sqrt{2 - x}} = \sqrt[4]{2 - x}

(-\infty,2]

g \circ f \ \Rightarrow \ g(f(x)) = g(\sqrt{x}) = \sqrt{2 - \sqrt{x}}

\begin{cases}
2 - \sqrt{x} \ge 0 \qquad x \ge 0 \qquad [0,4] \\
2 \ge \sqrt{x} \\
4 \ge x
\end{cases}

f \circ f \ \Rightarrow \ f(f(x)) = f(\sqrt{x}) = \sqrt{\sqrt{x}} = \sqrt[4]{x}

x \ge 0

g \circ g \ \Rightarrow \ g(g(x)) = g(\sqrt{2 - x}) = \sqrt{2 - \sqrt{2 - x}}

\begin{array}{c}
2 - x \ge 0 \\
x \le 2
\end{array}
\quad \text{y} \quad
\begin{array}{c}
2 - \sqrt{2 - x} \ge 0\\
2 \ge \sqrt{2 - x}
\end{array}
\quad \Rightarrow \quad
\begin{array}{c}
4 \ge 2 - x \\
x \ge -2
\end{array}
\quad [-2,2]

Si h(x) = x + 9 \quad g(x) = \cos x \quad f(x) = x^{2}

f \circ g \circ g = f(g(h(x))) = f(g(x + 9)) = f(\cos (x + 9)) = \cos^{2}(x + 9)

Funciones inversas

Las funciones inyectivas uno a uno con dominio A e imagen B poseen una función inversa con dominio B e imagen A.

f(x)=y \ \leftrightarrow \ f^{-1}(y)=x \quad *No confundir con [f(x)]^{-1} = \cfrac{1}{f(x)}

Sea f(x) = x^{5} + 2

\begin{array}{c c l l}
&(1) & y = f(x) = x^{5} + 2 & \text{Dominio } \mathbb{R} \ \text{Imagen } \mathbb{R} \\
\text{Despejar } x & (2) & x = \sqrt[5]{y - 2}& \mathbb{R} \land \mathbb{R} \\
& (3) & f^{-1}(x) = \sqrt[5]{x - 2} &
\end{array}

Sea f(x) = \cfrac{1 + 3x}{5 - 2x}

y = \cfrac{1 + 3x}{5 - 2x}

\downarrow

(5 - 2x)y = 1 + 3x

5y - 2xy = 1 + 3x

5y - 1 = 3x + 2xy = x(3 + 2y)

x = \cfrac{5y - 1}{2y + 3} \ \longrightarrow \ f^{-1}(x) = \cfrac{5x - 1}{2x + 3}

Es importante mencionar que las gráficas de las inversas son simétricas.

Transformación de funciones

Muchas veces al momento de añadir alguna constante sumando, restando, multiplicando o dividiendo a una función, nos preguntamos cómo se vería gráficamente cuando le agreguemos esa constante. Bien, es más fácil de lo que parece, y es lo que vamos a ver a continuación.

Desplazamiento horizontal y vertical

Empezaremos por desplazar las funciones horizontal y verticalmente, veamos la siguiente imagen:

Tenemos una función f(x), vamos a moverla de las siguientes maneras:

• Izquierda: para mover una función hacia la izquierda, se le tiene que sumar una constante al valor de x
• Derecha: para mover una función hacia la derecha, se le tiene que restar una constante al valor de x
• Arriba: para hacer que una función suba, hay que sumar una constante a toda la función
• Abajo: para hacer que una función baje, hay que restarle una constante a toda la función

Con eso ya estamos listos para mover nuestra función como nosotros querramos.

Ejemplo de desplazamiento horizontal y vertical de las funciones

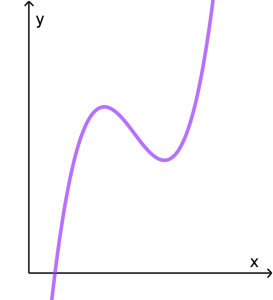
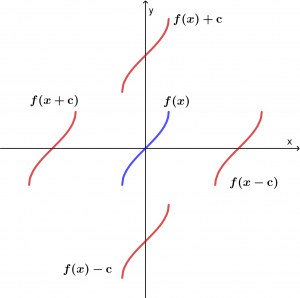
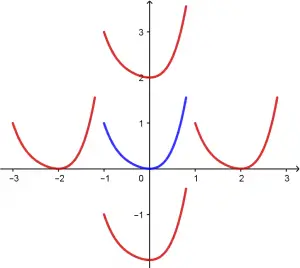
Tenemos la siguiente función f(x) = x^{4}+x^{3}+x^{2} (un la gráfica sólo se toma un pedazo de la función para que la gráfica se vea más limpia)

Y si nosotros queremos mover esa función una unidad a la izquierda, entonces tenemos que sumar a todas las x‘s el número 1, de igual manera si queremos mover a la derecha la función, a todas las x‘s se le tienen que restar el número 1. Para desplazar la función una unidad hacia arriba o hacia abajo, sólo hay que agregar una unidad que suma o reste a toda la función. Vamos a desplazarla

Desplazamiento hacia arriba: f(x) = x^{4}+x^{3}+x^{2}+2

Desplazamiento hacia abajo: f(x) = x^{4}+x^{3}+x^{2}-2

Desplazamiento hacia la izquierda: f(x) = (x+2)^{4}+(x+2)^{3}+(x+2)^{2}

Desplazamiento hacia la derecha: f(x) = (x-2)^{4}+(x-2)^{3}+(x-2)^{2}

Estiramientos y reflexiones

Es muy común que a veces veas funciones que se parezcan mucho o estén reflejadas con respecto al eje x o al eje y. Es muy fácil estirar, apretar o reflejar una función, lo veremos a continuación.

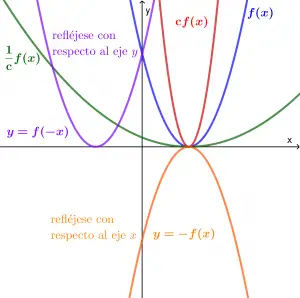
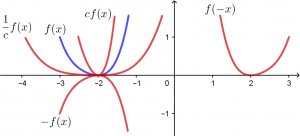
Observa la siguiente gráfica con nuestra función f(x):

• cf(x)  comprime la función
• \frac{1}{c}f(x) estira la función
• -f(x) refleja la función con respecto al eje x
• f(-x) refleja la función con respecto al eje y

Ejemplo de estiramientos y reflexiones de las funciones

Tomemos un trozo de la función f(x) = (x+2)^{4}+(x+2)^{3}+(x+2)^{2} y vamos a estirarla y a reflejarla:

• Función comprimida: 5(x+2)^{4}+5(x+2)^{3}+5(x+2)^{2}
• Función estirada: 0\text{.}1(x+2)^{4}+0\text{.}1(x+2)^{3}+0\text{.}1(x+2)^{2}
• Función reflejada con respecto al eje y: (-x+2)^{4}+(-x+2)^{3}+(-x+2)^{2}
• Función reflejada con respecto al eje x: -(x+2)^{4}-(x+2)^{3}-(x+2)^{2}

Modelamiento con funciones

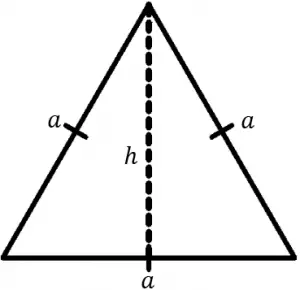
Ejemplo 1

P = \text{perímetro}

P = 3a

a = P/3

Del área A = b \times h / 2 \quad b = a = \cfrac{P}{3}

h = \sqrt{a^{2} - (1/2 \ a)^{2}} = \sqrt{a^{2} - \frac{1}{4} a^{2}} = \cfrac{\sqrt{3}}{2}a = \cfrac{\sqrt{3}}{3} \ \cfrac{P}{3} = \cfrac{P}{2\sqrt{3}}

A =\cfrac{1}{2} \bigg ( \cfrac{P}{3} \bigg ) \bigg ( \cfrac{1}{2\sqrt{3}} \bigg ) = \cfrac{1}{12\sqrt{3}} P^{2}

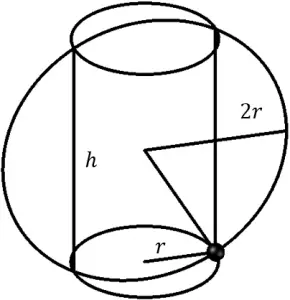
Ejemplo 2

h = \sqrt{4r^{2} - r^{2}} = \sqrt{3} r

2h = 2\sqrt{3}r

V(r) = \pi r^{2} \cdot 2 \sqrt{3} = 2\sqrt{3}r^{3}

Gracias por estar en este artículo con nosotros :)