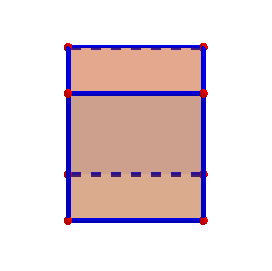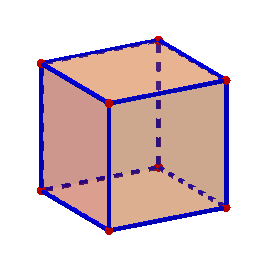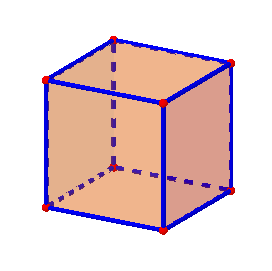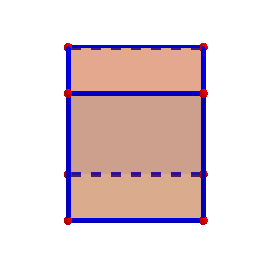
¿Qué es un poliedro?
Un poliedro es un sólido el cual está limitado sólo por superficies planas a las cuales llamamos con el nombre de caras, a las intersecciones de las caras se les llama aristas y a los puntos donde se cortan las aristas se les llama vértices. Se les llama diagonales a las líneas que unen vértices que no pertenecen a la misma cara.
¿Qué es un poliedro regular o un sólido platónico?
Como ya podrás imaginar, y seguramente ya lo habrás visto en la escuela, un poliedro regular o también llamado poliedros platónicos son aquellos que todas sus caras son polígonos regulares. En total sólo existen 5 poliedros regulares (5 sólidos platónicos) que seguro ya conoces, cada uno de estos sólidos regulares tienen el prefijo de la cantidad del número de caras. Los poliedros regulares para recortar y armar los encontrarás en el siguiente link de aquí. Veamos la figura desglosada de los poliedros regulares como se vería sin estar armada y luego veamos la figura armada de cada poliedro regular:
Tetraedro regular (sólido platónico de 4 caras)
Cuántas caras tiene un tetraedro regular
El tetraedro regular tiene un total de 4 caras.
Cuántos vértices tiene un tetraedro regular
Un tetraedro regular tiene un total de 4 vértices.
Cuántas aristas tiene un tetraedro regular
Un tetraedro regular tiene un total de 6 aristas.
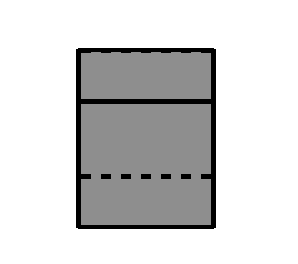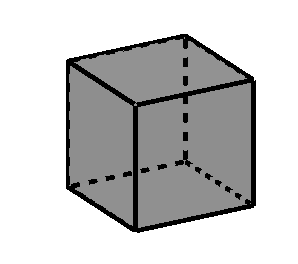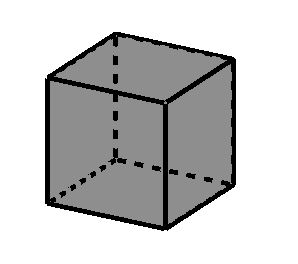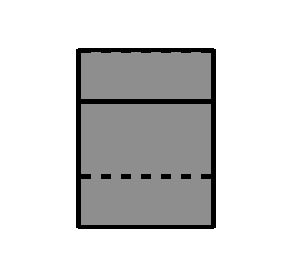
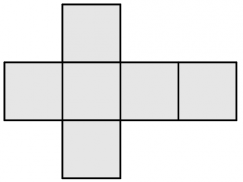
Hexaedro regular o cubo (sólido platónico de 6 caras)
Cuántas caras tiene un hexaedro regular
El hexaedro regular tiene un total de 6 caras.
Cuántos vértices tiene un hexaedro regular
Un hexaedro regular tiene un total de 8 vértices.
Cuántas aristas tiene un hexaedro regular
Un hexaedro regular tiene un total de 12 aristas.

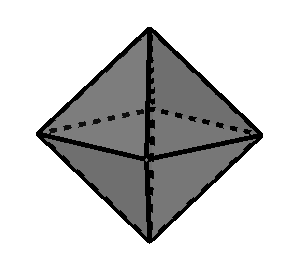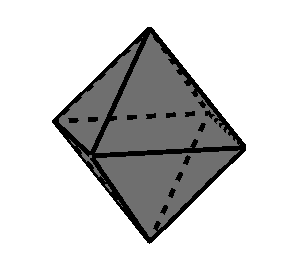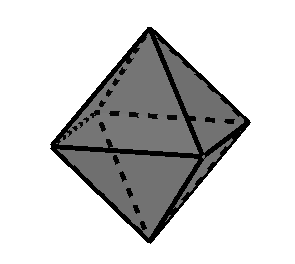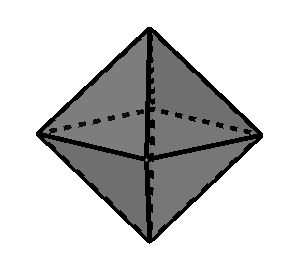
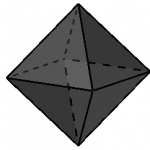
Octaedro regular (sólido platónico de 8 caras)
Cuántas caras tiene un octaedro regular
El octaedro regular tiene un total de 8 caras.
Cuántos vértices tiene un octaedro regular
Un octaedro regular tiene un total de 6 vértices.
Cuántas aristas tiene un octaedro regular
Un octaedro regular tiene un total de 12 aristas.
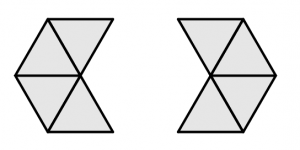
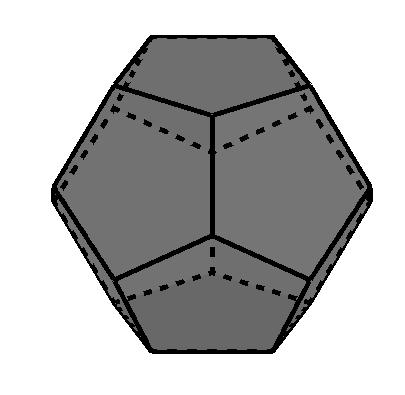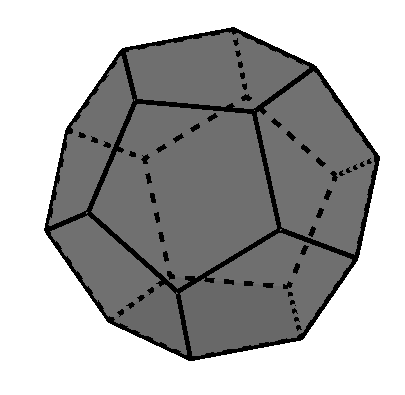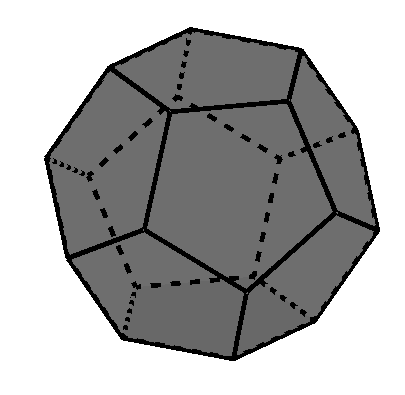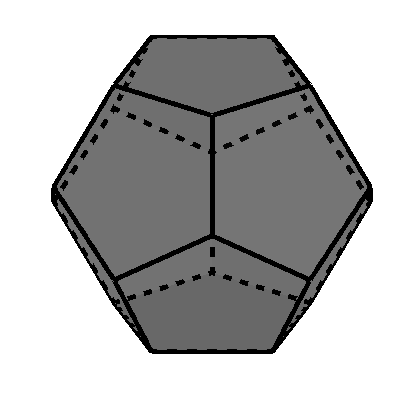
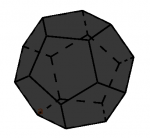
Dodecaedro regular (sólido platónico de 12 caras)
Cuántas caras tiene un dodecaedro regular
El dodecaedro regular tiene un total de 12 caras.
Cuántos vértices tiene un dodecaedro regular
Un dodecaedro regular tiene un total de 20 vértices.
Cuántas aristas tiene un dodecaedro regular
Un dodecaedro regular tiene un total de 30 aristas.
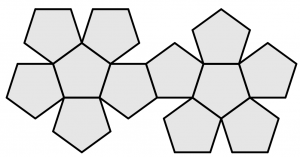
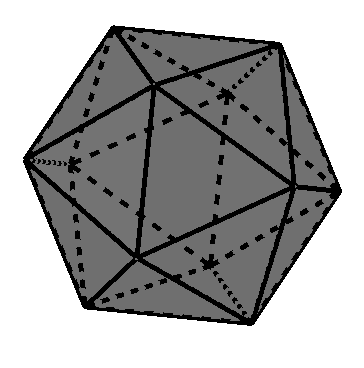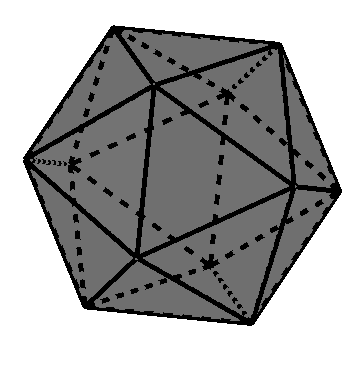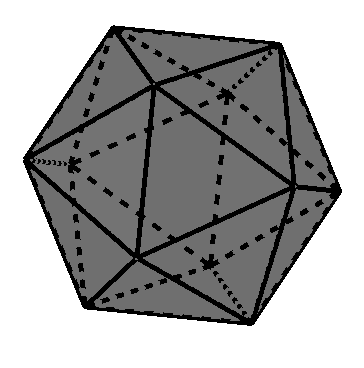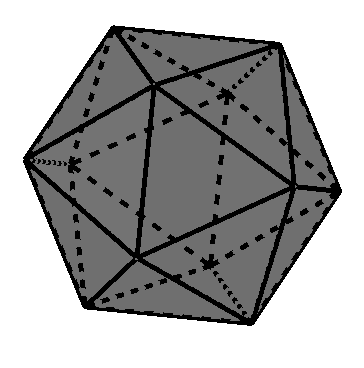
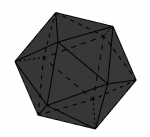
Icosaedro regular (sólido platónico de 20 caras)
Cuántas caras tiene un icosaedro regular
El icosaedro regular es un poliedro regular que consta de 20 caras.
Cuántos vértices tiene un icosaedro regular
Un icosaedro regular tiene un total de 12 vértices.
Cuántas aristas tiene un icosaedro regular
Un icosaedro regular tiene un total de 30 aristas.
Áreas y volúmenes de los poliedros regulares
Primero hay que tener en cuenta lo siguiente para poder calcular el área, volumen y radios de los poliedros regulares presentados, es un pequeño glosario de términos:
A = área
V = volumen
a = arista
R = radio de la esfera circunscrita
r = radio de la esfera inscrita
\rho = radio de la esfera tangente a las aristas
Fórmula para el cálculo del área, volumen y radios de un tetraedro
Área de un tetraedro regular
A = a^{2}\sqrt{3} = \cfrac{8}{3} \ R^{2}\sqrt{3} = 24r^{2} \sqrt{3} = 8 \rho \sqrt{3}
Volumen de un tetraedro regular
V = \cfrac{a^{3}}{12} \sqrt{2} = \cfrac{8}{27} \ R^{3}\sqrt{3} = 8r^{3} \sqrt{3} = \cfrac{8}{3} \ \rho^{3}
Radios de un tetraedro regular
R = \cfrac{a}{4} \sqrt{6} , \quad r = \cfrac{a}{12}\sqrt{6}
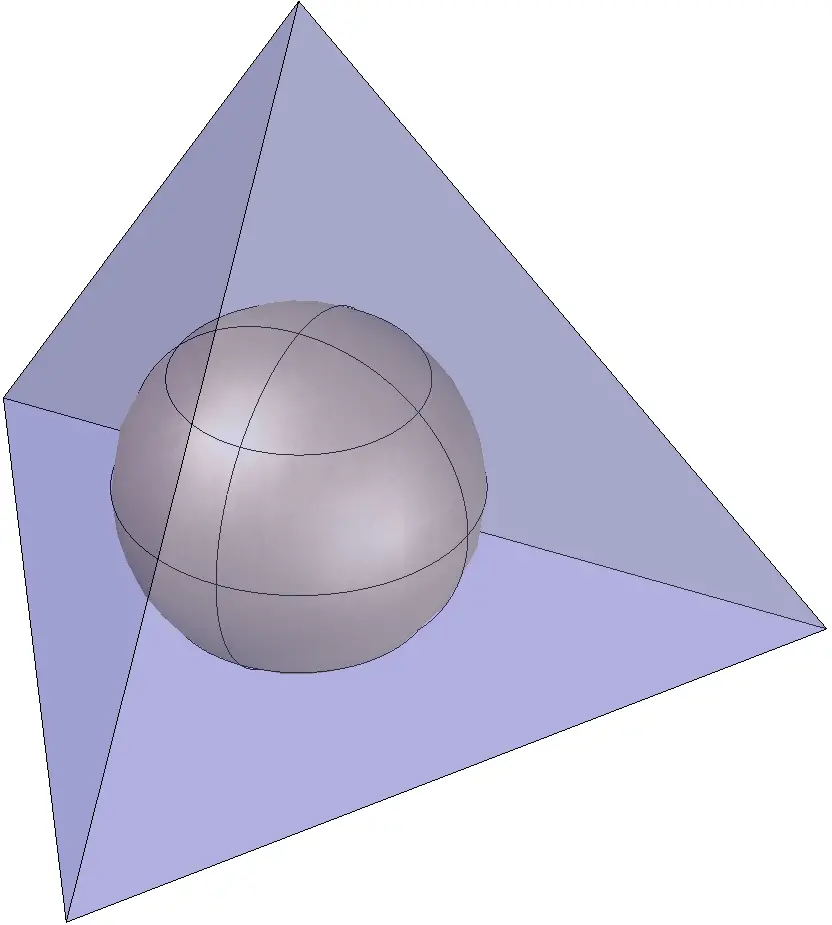
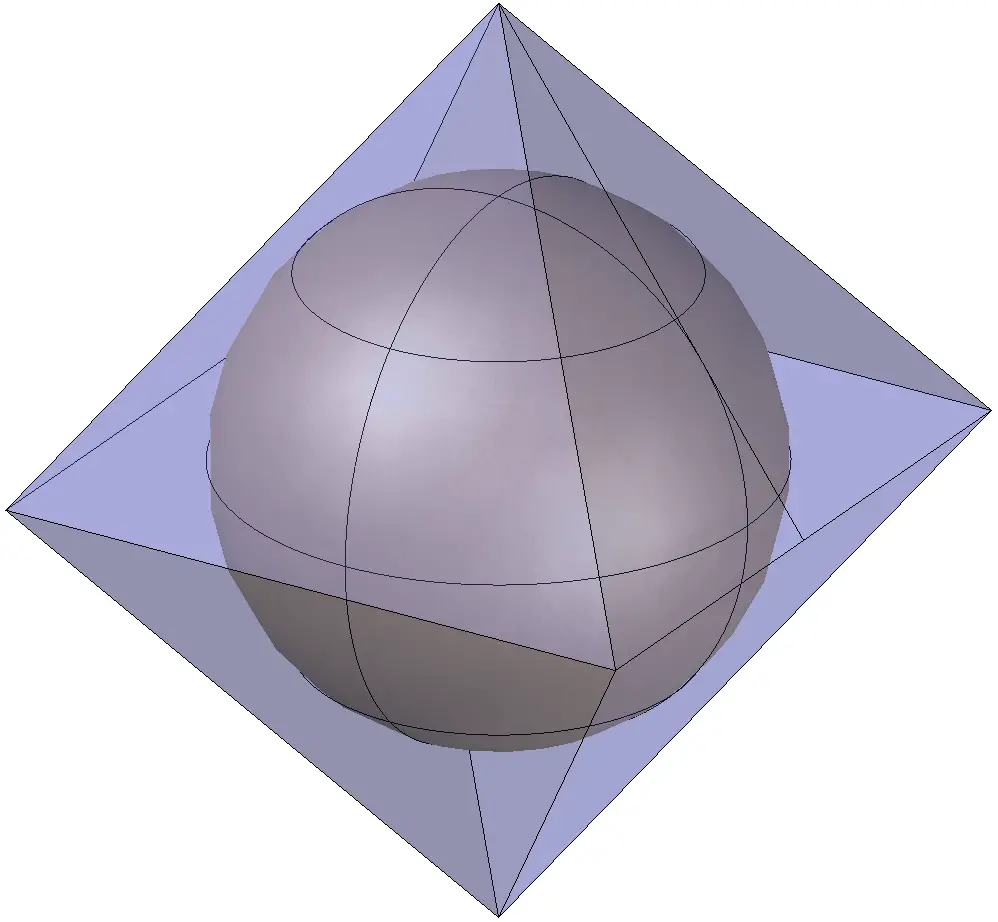
Tetraedro circunscrito a la esfera
Tetraedro inscrito en la esfera
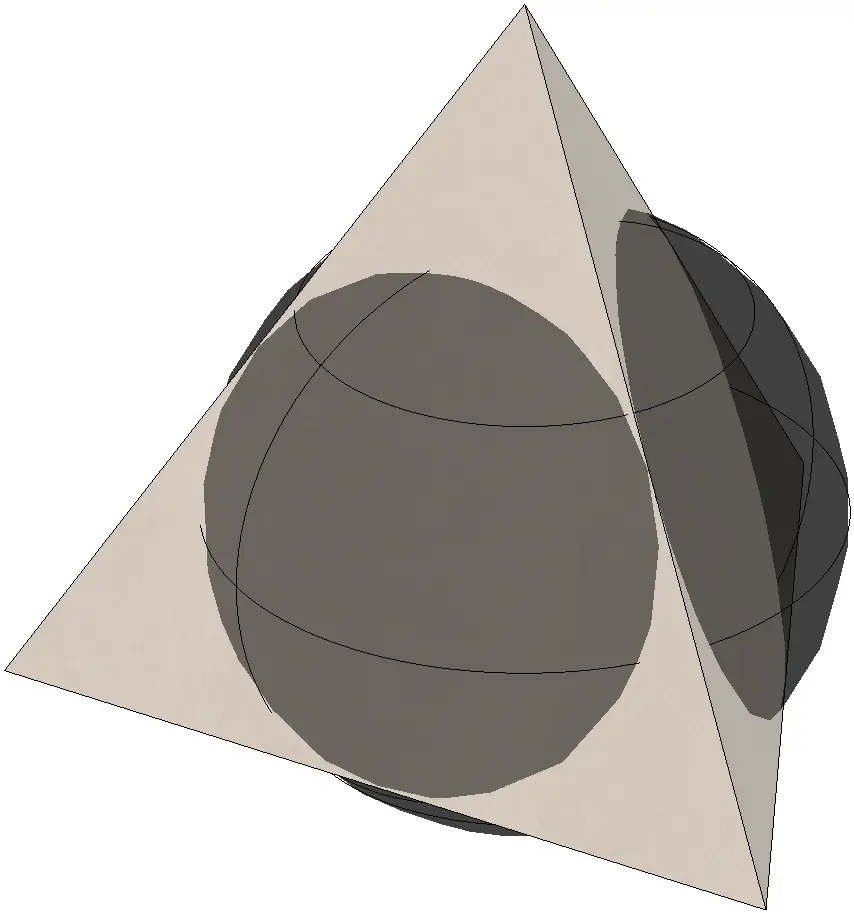
Tatraedro tangente a la esfera
Fórmulas para el cálculo del área, volumen y radios de un hexaedro o cubo
Área de un cubo o hexaedro regular
A = 6a^{2} = 8R^{2} = 24r^{2} = 12 \rho ^{2}
Volumen de un cubo o hexaedro regular
V = a^{3} = \cfrac{8}{9} \ R^{3}\sqrt{3} = 8r^{3} = 2\rho^{3}\sqrt{2}
Radios de un cubo o hexaedro regular
R = \cfrac{a}{2}\sqrt{3}, \quad r = \cfrac{a}{2}
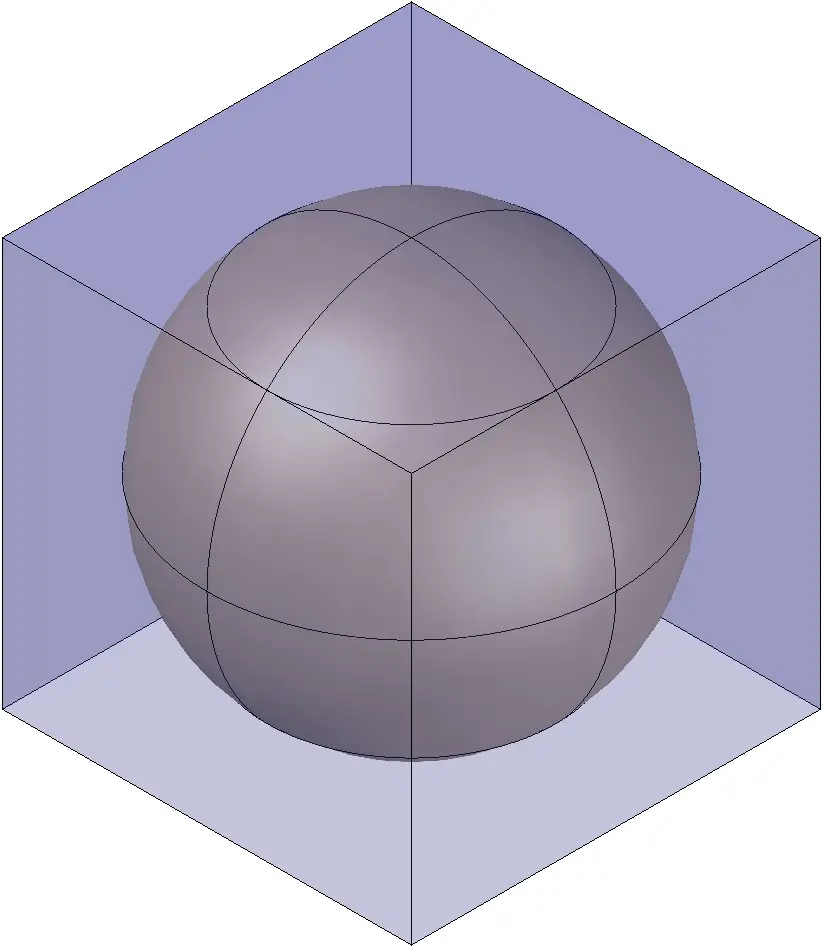
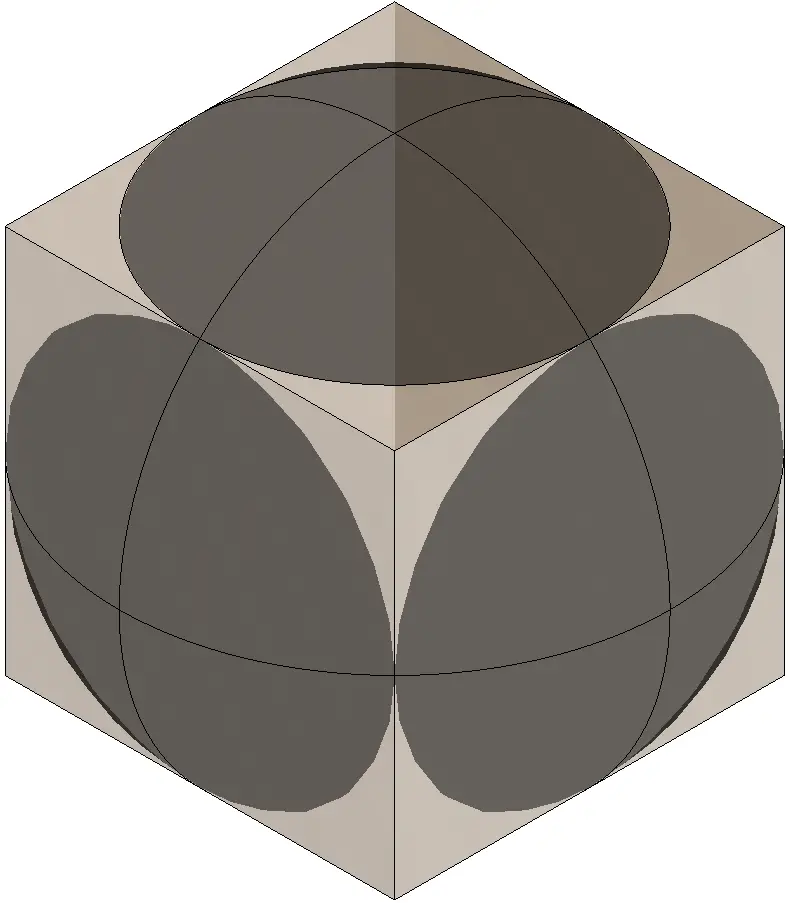
Cubo circunscrito a la esfera
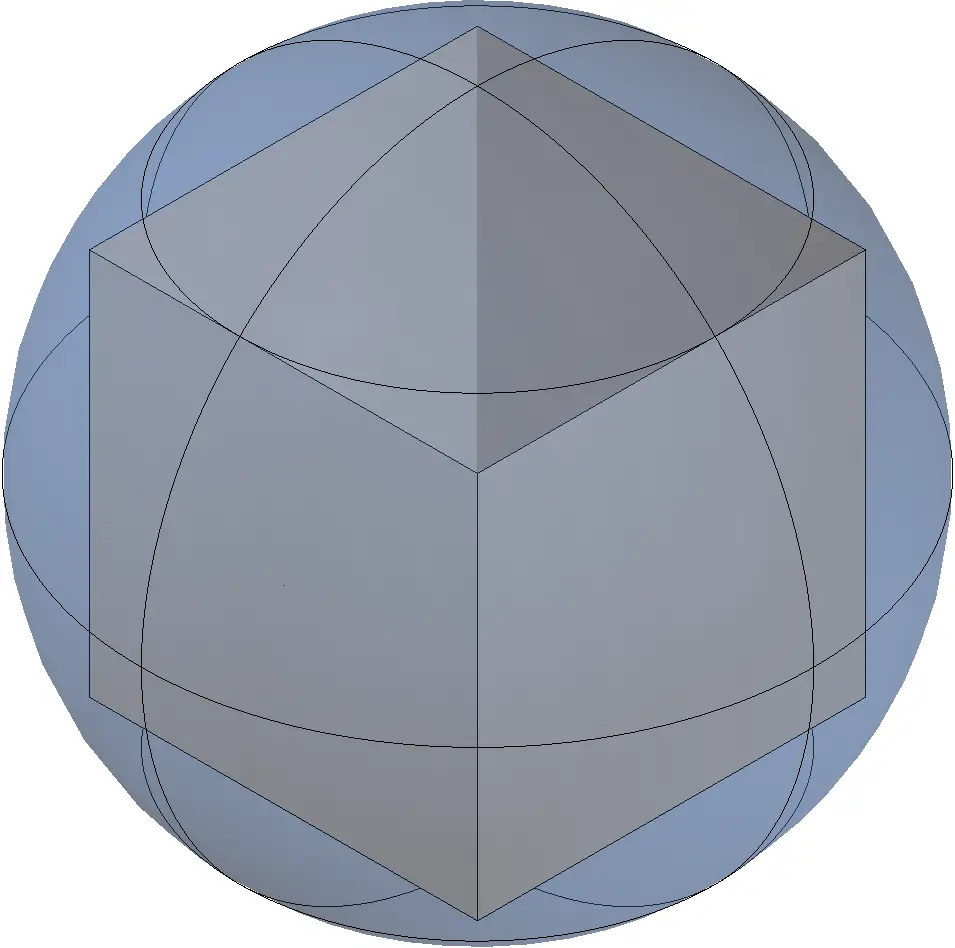
Cubo inscrito en la esfera
Cubo tangente a la esfera
Fórmulas para el cálculo del área, volumen y radios de un octaedro
Área de un octaedro regular
A = 2a^{3}\sqrt{3} = 4R^{2} \sqrt{3} = 12r^{2}\sqrt{3} = 8 \rho ^{2}\sqrt{3}
Volumen de un octaedro regular
V = \cfrac{a^{3}}{3}\sqrt{2} = \cfrac{4}{3} \ R^{3} = 4 r^{3} \sqrt{3} = \cfrac{8}{3} \ \rho^{3} \sqrt{2}
Radios de un octaedro regular
R = \cfrac{a}{2}\sqrt{2}, \quad r = \cfrac{a}{6}\sqrt{6}
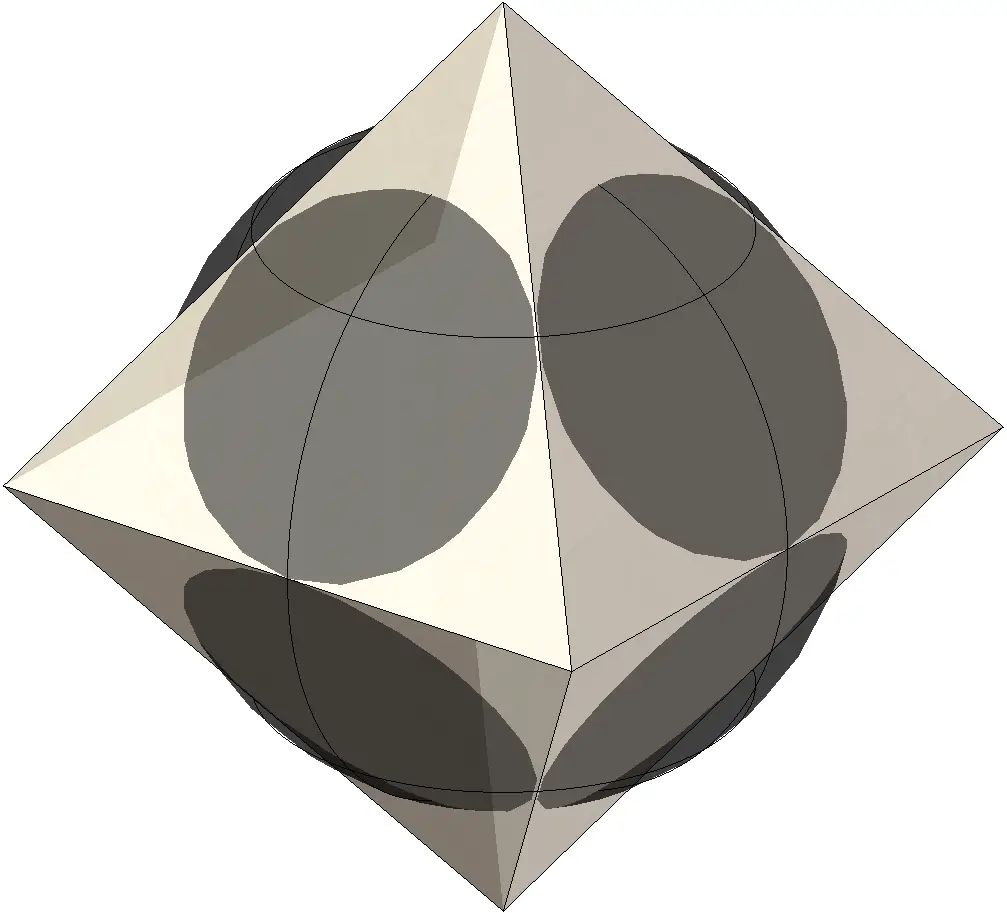
Octaedro circunscrito a la esfera
Octaedro inscrito en la esfera
Octaedro tangente a la esfera
Fórmula para el cálculo del área, volumen y radios de un dodecaedro
Área de un dodecaedro regular
A = 3 a^{2}\sqrt{5 \left ( 5 + 2\sqrt{5} \right ) } = 2 R^{2} \sqrt{10 \left ( 5 - \sqrt{5} \right )}
A = 30r^{2} \sqrt{2\left ( 65 - 29 \sqrt{5} \right )} = 6\rho^{2}\sqrt{10 \left (25 - 11 \sqrt{5} \right )}
Volumen de un dodecaedro regular
V = \cfrac{a^{3}}{4} \left ( 15 + 7\sqrt{5} \right ) = \cfrac{2 R^{3}}{9}\left ( 5\sqrt{3} + \sqrt{15} \right )
V = 10r^{3} \sqrt{2 \left ( 65 - 29\sqrt{5} \right )} = 2\rho^{3} \left ( 3\sqrt{5} - 5\right )
Radios de un dodecaedro regular
R = \cfrac{a}{4}\left ( \sqrt{3} + \sqrt{15} \right ), \quad r = \cfrac{a}{20}\sqrt{10 \left ( 25 + 11 \sqrt{5} \right )}
Dodecaedro circunscrito a la esfera
Dodecaedro inscrito en la esfera
Dodecaedro tangente a la esfera
Fórmulas para el cálculo del área, volumen y radios de un icosaedro regular
Área de un icosaedro regular
A = 5a^{2} \sqrt{3} = 2R^{2}\sqrt{3} \left ( 5 - \sqrt{5} \right )
A = 30r^{2}\sqrt{3} \left ( 7 - 3\sqrt{5} \right ) = 10 \rho^{2}\sqrt{3}\left ( 3 - \sqrt{5} \right )
Volumen de un icosaedro regular
V = \cfrac{5a^{3}}{12} \left ( 3 + \sqrt{5} \right ) = \cfrac{2R^{3}}{3} \left ( \sqrt{10 + 2\sqrt{5}}\right )
V = 10r^{3} \sqrt{3} \left ( 7 - 3 \sqrt{5} \right ) = \cfrac{10 \rho^{3}}{3}\left ( \sqrt{5} - 1 \right )
Radios de un icosaedro regular
R = \cfrac{a}{4} \sqrt{10 + 2 \sqrt{5}}, \quad r = \cfrac{a\sqrt{3}}{12} \left ( 3 + \sqrt{5} \right )
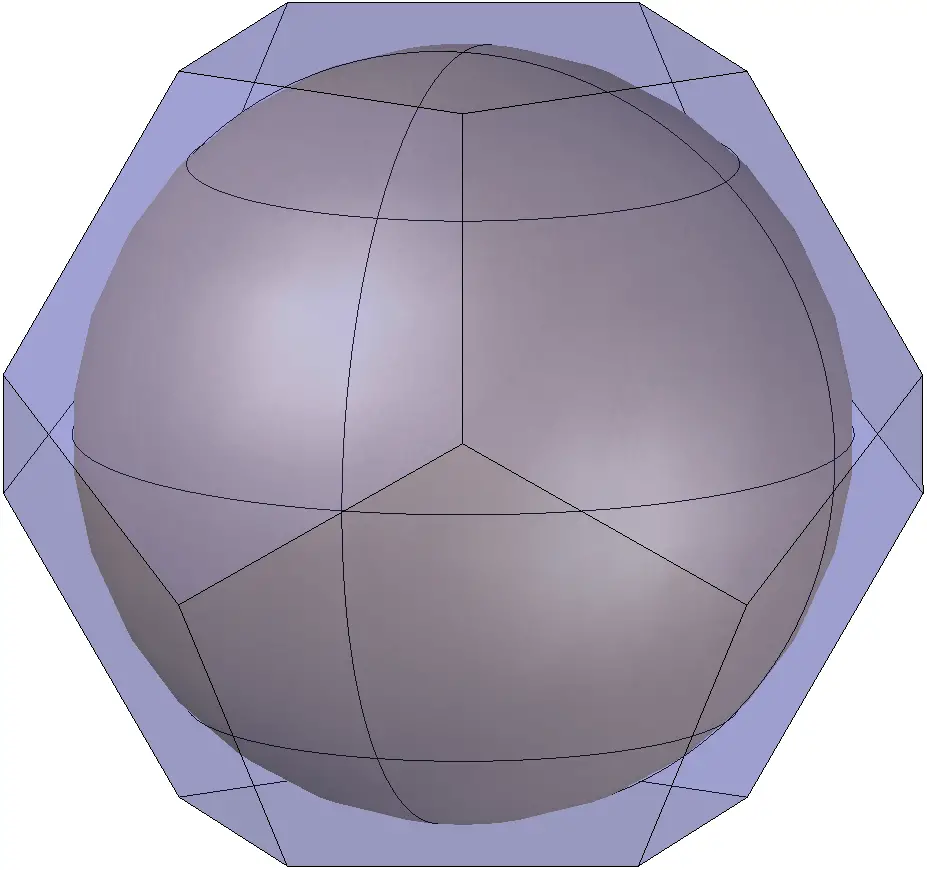
Icosaedro inscrito en la esfera
Icosaedro inscrito en la esfera más realista
Las fórmulas mencionadas anteriormente se tomaron de la siguiente referencia:
Spiegel, M. (1999). Manual de fórmulas y tablas matemáticas, D.F.,México, McGRAW-HILL.
Gracias por estar en este momento con nosotros : )