Con los estudios en la escuela, es muy recomendable que tengas un buen juego de geometría para que todas tus figuras salgan perfectas.
Definición de las rectas paralelas
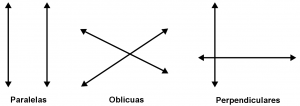
Dos rectas son paralelas si no se intersecan por más que se prolonguen. A continuación veremos en la siguiente imagen ejemplos de paralelas, oblicuas y perpendiculares.
Cuando dos rectas se cruzan sin importar la medida de los ángulos que se forman en ellas, son rectas oblicuas. También se le conoce como líneas secantes.
Cuando dos rectas se cruzan y forman ángulos de 90 grados entre ellas, se les considera rectas oblicuas y rectas perpendiculares. Como bien se dice: toda recta perpendicular es oblicua, pero no toda recta oblicua es perpendicular. Así es como decimos que es secante perpendicular cada recta. Continuemos hablando de rectas paralelas y perpendiculares y de rectas que se cortan por una que no es perpendicular.
Propiedades de las líneas paralelas
Las 3 propiedades que tienen las rectas paralelas son las siguientes:
Son simétricas o recíprocas
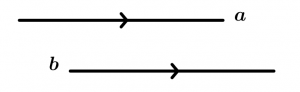
Esta propiedad dice que si una recta a es paralela a una recta b, entonces la recta b es paralela a la recta a.
\text{Si } \ a \parallel b \ \text{ entonces } b \parallel a
Son transitivas
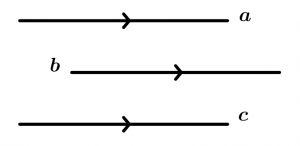
Si una recta a es paralela a una recta b y la recta b es paralela a una recta c, entonces la recta c es paralela a la recta a.
\text{Si } \ a \parallel b \ \text{ y } \ b \parallel c \ \text{ entonces } \ c \parallel a
Idéntica o reflexiva
Esta propiedad nos dice que toda recta es paralela a sí misma.
a \parallel a
Postulados de las rectas paralelas
Postulado de Euclides (de las paralelas)
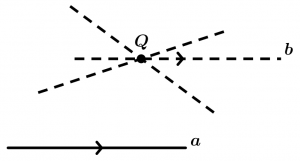
Por un punto Q fuera de una recta a pasa una y sólo una paralela a dicha recta.
Este postulado quiere decir que por el punto Q sólo va a pasar únicamente una recta paralela, no pueden pasar más de dos rectas paralelas en el punto Q.
Postulado de rectas cortadas por una secante o transversal
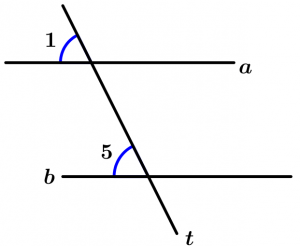
Si dos rectas a y b son cortadas por una recta transversal t y un par de ángulos correspondientes son congruentes, entonces las rectas a y b son paralelas.
\text{Si } \ \measuredangle 1 \cong \measuredangle 5
\text{entonces } \ a \parallel b
Todas las rectas t que cortan a las rectas paralelas se consideran rectas transversales. Ahora sí podemos decir que son rectas paralelas cortadas por una transversal.
Teoremas sobre rectas paralelas y transversales
Estos teoremas también los conocemos como propiedades de rectas paralelas cortadas por una transversal. En las tareas escolares es muy recomendable que tengas un juego de geometría para que los trazos salgan perfectos y puedas trazar perfectamente línea paralelas y perpendiculares.
Teorema 1
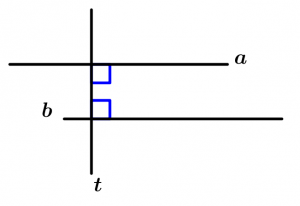
Si dos rectas a y b son perpendiculares a una recta t, entonces a y b son paralelas. Teniendo rectas paralelas y perpendiculares en un mismo diagrama, como en el teorema 3.
\text{Si } \ a \bot t \ \text{ y } \ b \bot t
\text{entonces } \ a \parallel b
La línea a es una línea paralela y perpendicular al igual que la línea b.
Teorema 2
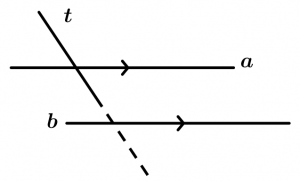
Si una recta t corta a otra, corta también a cualquier paralela a ésta.
Teorema 3
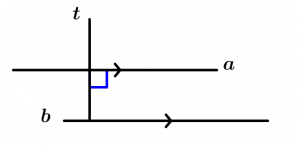
Cualquier línea perpendicular a una recta, es perpendicular a cualquier línea paralela a ésta. Teniendo paralelo y perpendicular en un mismo diagrama, como en el teorema 1.
\text{Si } \ a \parallel b \ \text{ y } \ a \bot t
\text{entonces } \ b \bot t
Antes de continuar con los teoremas
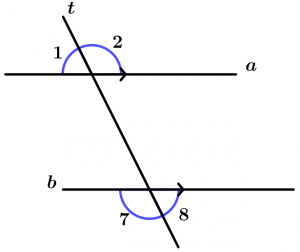
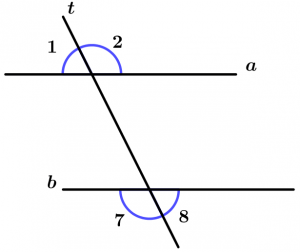
Antes de continuar con los teoremas, tenemos que dejar en claro algunos conceptos, son sencillos pero necesarios. Veremos los ángulos internos, los ángulos externos, ángulos correspondientes, ángulos alternos internos, ángulos conjugados internos y los ángulos conjugados externos. Vamos a los ejemplos.
Ángulos internos
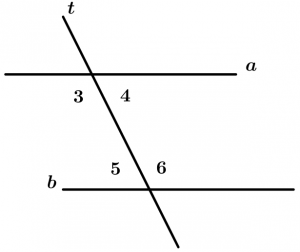
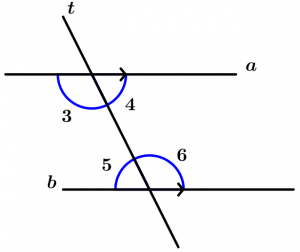
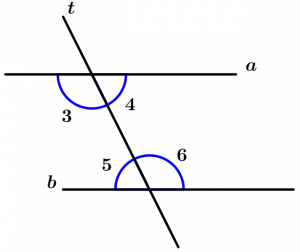
Son aquellos ángulos que quedan entre las dos rectas que son cortadas por la recta transversal, éstos ángulos son el 3, 4, 5 y 6.
\measuredangle 3, \measuredangle 4, \measuredangle 5 \ \text{ y } \ \measuredangle 6
\text{son ángulos internos}
Ángulos externos
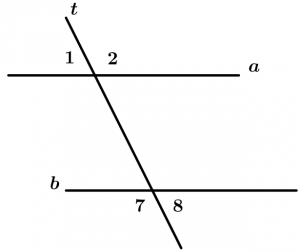
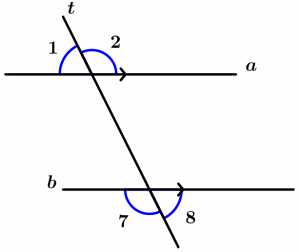
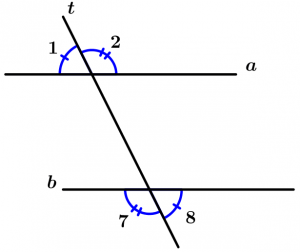
Son aquellos ángulos que no quedan entre las dos rectas y que son cortadas por la línea transversal, éstos ángulos son el 1, 2, 7 y 8.
\measuredangle 1, \measuredangle 2, \measuredangle 7 \ \text{ y } \measuredangle 8
\text{son ángulos externos}
Ángulos correspondientes
Son todos aquellos ángulos que están ubicados del mismo lado de la transversal, uno es interno y el otro es externo, se agrupan por pares los cuales son 4.
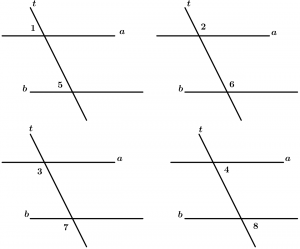Los pares de ángulos correspondientes son:
\text{Par 1: } \ \measuredangle 1 \text{ y }\measuredangle 5
\text{Par 2: } \ \measuredangle 2 \text{ y }\measuredangle 6
\text{Par 3: } \ \measuredangle 3 \text{ y }\measuredangle 7
\text{Par 4: } \ \measuredangle 4 \text{ y }\measuredangle 8
Ángulos alternos internos
Son dos ángulos internos con diferente vértice y que están en lados diferentes de la transversal, se agrupan por pares y hay 2.
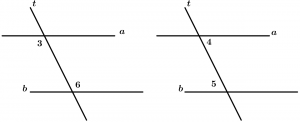Pares de ángulos alternos internos:
\text{Par 1: } \ \measuredangle 3 \text{ y }\measuredangle 6
\text{Par 2: } \ \measuredangle 4 \text{ y }\measuredangle 5
Ángulos alternos externos
Son dos ángulos exteriores con diferente vértice y que están en lados diferentes de la transversal, se agrupan por pares y son 2.
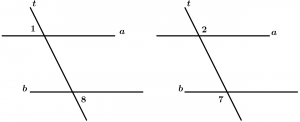Pares de ángulos alternos externos:
\text{Par 1: } \ \measuredangle 1 \text{ y }\measuredangle 8
\text{Par 2: } \ \measuredangle 2 \text{ y }\measuredangle 7
Ángulos conjugados internos
Son dos ángulos internos con diferente vértice y que están en el mismo lado de la transversal, se agrupan por pares y son 2.
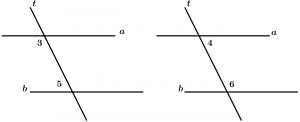Pares de ángulos conjugados internos:
\text{Par 1: } \ \measuredangle 3 \text{ y }\measuredangle 5
\text{Par 2: } \ \measuredangle 4 \text{ y }\measuredangle 6
Ángulos conjugados externos
Son dos ángulos externos con diferente vértice y que están en el mismo lado de la transversal, se agrupan por pares y son 2.
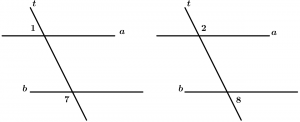Pares de ángulos conjugados externos:
\text{Par 1: } \ \measuredangle 1 \text{ y }\measuredangle 7
\text{Par 2: } \ \measuredangle 2 \text{ y }\measuredangle 8
Teorema 4
Si una recta a y b son cortadas por una recta transversal t y resulta que un par de ángulos alternos internos son congruentes, entonces las rectas a y b son paralelas.
\text{Si un enunciado dice que } \ \measuredangle 3 \cong \measuredangle 6
\text{o que } \ \measuredangle 4 \cong \measuredangle 5
\text{entonces } \ a\parallel b
Teorema 5. El teorema PAI
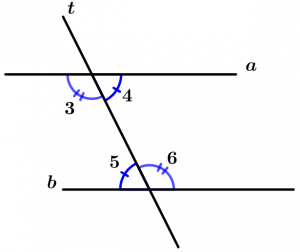
Si dos rectas paralelas a y b se cortan por una recta transversal t, entonces los ángulos alternos internos son congruentes.
\text{Si } \ t \ \text{ corta a las paralelas } a \ \text{ y } \ b
\text{entonces } \ \measuredangle 3\cong \measuredangle 6 \ \text{ y } \ \measuredangle 4 \cong \measuredangle 5
Teorema 6
Cualquier recta transversal t forma con dos rectas paralelas a y b, ángulos alternos externos congruentes.
\text{Si } \ t \ \text{ corta a las rectas paralelas} \ a \ \text{ y } \ b
\text{entonces } \ \measuredangle 1 \cong \measuredangle 8 \ \text{ y } \ \measuredangle 2 \cong \measuredangle 7
Teorema 7
Si dos rectas a y b se cortan por una recta transversal t y un par de ángulos alternos externos son congruentes, entonces las rectas a y b son paralelas.
\text{Si } \ a \ \text{ y } \ b \ \text{ se cortan por } \ t
\text{ y el enunciado dice que } \ \measuredangle 1 \cong \measuredangle 8 \text{ o que }
\measuredangle 2 \cong \measuredangle 7 \ \text{ entonces}
a \parallel b
Teorema 8
Toda recta transversal t forma con dos rectas paralelas a y b ángulos correspondientes congruentes.
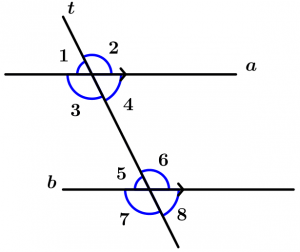Pares de ángulos correspondientes congruentes:
\text{Par 1: } \ \measuredangle 1 \text{ y }\measuredangle 5
\text{Par 2: } \ \measuredangle 2 \text{ y }\measuredangle 6
\text{Par 3: } \ \measuredangle 3 \text{ y }\measuredangle 7
\text{Par 4: } \ \measuredangle 4 \text{ y }\measuredangle 8
Teorema 9
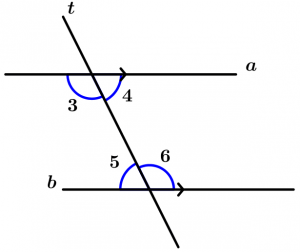
Si dos rectas paralelas a y b son cortadas por una recta transversal t, entonces los ángulos conjugados internos son suplementarios.
\text{Si las rectas paralelas} \ a \ \text{ y } \ b
\text{son cortadas por } \ t, \ \text{ entonces}
\measuredangle 3 + \measuredangle 5 = 180^{\text{o}} \ \text{ y}
\measuredangle 4 + \measuredangle 6 = 180^{\text{o}}
Teorema 10
Si dos rectas a y b se cortan por una recta transversal t y los ángulos conjugados internos son suplementarios, entonces las rectas a y b son paralelas.
\text{Si las rectas } \ a \ \text{ y } \ b \ \text{son cortadas por }
t \ \text{ y el enunciado dice que:}
\measuredangle 3 + \measuredangle 5 = 180^{\text{o}} \ \text{ o que}
\measuredangle 4 + \measuredangle 6 = 180^{\text{o}}
\text{entonces } \ a \parallel b
Teorema 11
Si dos rectas paralelas a y b son cortadas por una recta transversal t, entonces los ángulos conjugados externos son suplementarios.
\text{Si las rectas paralelas} \ a \ \text{ y } \ b
\text{son cortadas por } \ t, \ \text{ entonces}
\measuredangle 1 + \measuredangle 7 = 180^{\text{o}} \ \text{ y}
\measuredangle 2 + \measuredangle 8 = 180^{\text{o}}
Teorema 12
Si dos rectas a y b se cortan por una recta transversal t y los ángulos conjugados externos son suplementarios, las rectas a y b son paralelas.
\text{Si las rectas } \ a \ \text{ y } \ b \ \text{son cortadas por }
t \ \text{ y el enunciado dice que:}
\measuredangle 1 + \measuredangle 7 = 180^{\text{o}} \ \text{ o que}
\measuredangle 2 + \measuredangle 8 = 180^{\text{o}}
\text{entonces } \ a \parallel b
Teorema 13
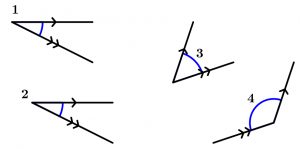
Si dos ángulos tienen sus lados respectivamente paralelos, éstos ángulos son congruentes o suplementarios.
\measuredangle 1 \cong \measuredangle 2
\measuredangle 3 + \measuredangle 4 = 180^{\text{o}}
Teorema 14, 15, 16
14. La suma de las medidas de los ángulos internos de un triángulo es igual a 180°.
\measuredangle A + \measuredangle B + \measuredangle C = 180^{\text{o}}
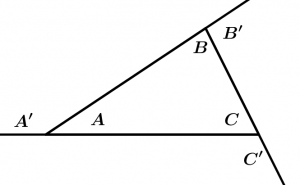
15. La suma de las medidas de los ángulos exteriores de un triángulo es igual a 360°.
\measuredangle A' + \measuredangle B' + \measuredangle C' = 360^{\text{o}}
16. La medida de todo ángulo exterior de un triángulo es igual a la suma de las medidas de los dos ángulos interiores no adyacentes.
\measuredangle A' = \measuredangle B + \measuredangle C
\measuredangle B' = \measuredangle A + \measuredangle C
\measuredangle C' = \measuredangle A + \measuredangle B
Recuerda que aquí puedes obtener un juego de geometría para aplicar a la perfección los teoremas.
Gracias por estar en este momento con nosotros : )
