Vamos de una vez con la definición, luego veremos unas características, después mencionaremos teoremas con sus propiedades de los logaritmos y por último dos ejemplos de logaritmos.
Definición de logaritmo
El logaritmo de un número con una base dada es el exponente al cual se debe de elevar la base para obtener el número.
Vamos a explicar un poco más esta definición. Tenemos que la relación que existe entre las funciones exponenciales y logarítmicas es que los logaritmos son la función inversa de las exponenciales, por lo tanto, si nosotros tenemos una función exponencial como por ejemplo:
y = b^{x}
El logaritmo de esa función que también se le puede llamar como la inversa es:
\log_{b}y = x
Pero como estamos acostumbrados a manejar a x como los números y a y como la función, la escribimos de la siguiente forma:
y = \log_{b}x
Como se puede ver en la Figura 1, se pueden apreciar las funciones exponenciales con sus respectivas funciones inversas o logarítmicas.
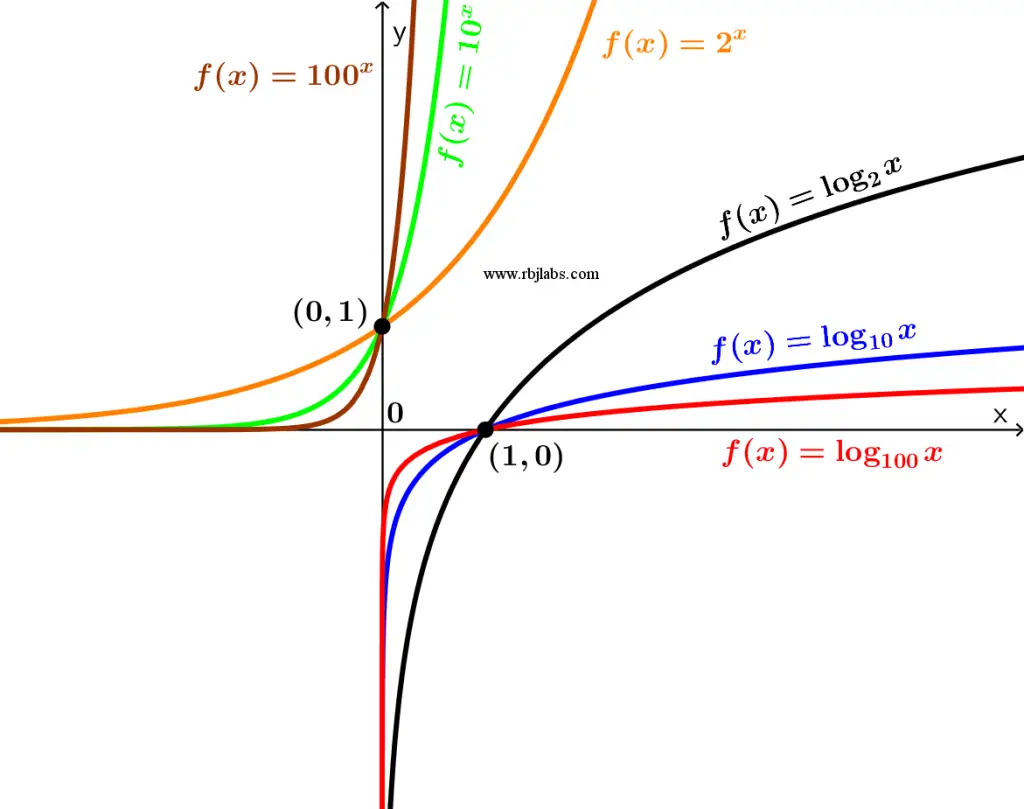
Continuando con la explicación, si tenemos la siguiente expresión:
\text{(1)} \quad \quad 6 = 2^{x}
Para que nosotros podamos hallar el valor de x necesitamos entender que x se encuentra entre los valores de 2 y 3 ya que 2^{2}=4 y 2^{3} = 8, a partir de aquí empezaremos a tantear valores para acercarnos a nuestro valor de 6. Es por eso que tenemos los logaritmos dado que los logaritmos también son exponentes. Teniendo como representación lo siguiente:
\text{(2)} \quad \quad \log_{2}6 = x
Así mismo, la única forma de hallar exactamente el valor de x es haciendo muchas iteraciones de la expresión \text{(1)}, como habíamos explicado de ir probando valores entre 2 y 3 hasta que tengamos un número con muchos decimales.
Es por eso que el valor de x se representa como \log_{2}6 y no como un número con muchos decimales. Claro que si agarras tu calculadora y pones \log_{2}6 te dará como resultado 2.5849..., el cual es un valor aproximado pero muy muy cercano al resultado ya que la calculadora hace iteraciones para darte tu respuesta, sólo que la calculadora puede hacer muchas iteraciones en menos de un segundo.
La única forma de tener el valor exacto es hacer infinitas iteraciones, pero eso nos tomaría una infinidad de tiempo. Es lo curioso de las matemáticas.
Características de los logaritmos
Los logaritmos tienen muchas peculiaridades como en muchos temas en el álgebra y ahora te voy a mostrar esas características que tienen los logaritmos para cuando vayas a realizar tus tareas de la escuela.
- Solamente tienen logaritmos reales los números positivos. Los números negativos no existen en el ámbito de los logaritmos, tales logaritmos de números reales son números complejos y además el logaritmo de cero no está definido.
- Cuando un número x aumenta, su logaritmo b también. Y cuando x tiende a infinito, b también. Así que podemos escribir lo siguiente:
\underset{x \to \infty} \lim \; \log_{b}x = \infty
- Para x < 1, \log_{b} x < 0; para x = 1, \log_{b} x = 0; y para x > 1, \log_{b} x > 0
- Cuando x tiende a cero, su logaritmo tiende hacia menos infinito, el cual se escribe de la siguiente forma
\underset{ x \to 0} \lim \; \log_{b}x = - \infty
Propiedades de los logaritmos
Las propiedades de los logaritmos las veremos en los siguientes teoremas, que son resultados de transformar cuatro leyes de los exponentes:
- b^{x}\cdot b^{y} = b^{x+y}
- b^{x} \div b^{y} = b^{x-y}
- \left(b^{x} \right)^{n} = b^{nx}
- n\sqrt{b^{x}} = b^{x/n}
De los cuales nosotros escribiremos lo siguiente
M = b^{x} \qquad \text{y} \qquad N=b^{y}
de donde:
x = \log_{b}M \qquad \text{y} \qquad y = \log_{b} N
Teorema 1
El logaritmo del producto o de la multiplicación de dos números positivos es igual a la suma de los logaritmos de cada número.
\log_{b}MN = \log_{b}M + \log_{b}N
Si tienes como número una multiplicación, puedes tranquilamente separarlo como una suma de logaritmos.
Teorema 2
El logaritmo del cociente de dos números positivos es igual al logaritmo del dividendo menos el logaritmo del divisor.
\log_{b}\cfrac{M}{N} = \log_{b}M - \log_{b}N
Tal y como se logra apreciar, si tu número es una división, puedes pasarlo a una resta de logaritmos, nada más recuerda que siempre va a ser el logaritmo del numerador menos el logaritmo del denominador. No los vayas a colocar al revés porque eso es incorrecto.
Teorema 3
El logaritmo de la enésima potencia de un número positivo es igual a n veces el logaritmo del número.
\log_{b}M^{n} = n\log_{b}M
Lo conocemos como bajar el exponente, esta es una de las ventajas que nos dan los logaritmos, que podemos bajar el exponente que tiene nuestro número y que pase multiplicando a todo el logaritmo.
Teorema 4
El logaritmo de la raíz enésima positiva real de un número positivo es igual al resultado de dividir entre n el logaritmo del número.
\log_{b}M^{n/a} = \cfrac{n}{a}\log_{b}M = \log_{b}\sqrt[a]{M^{n}}
Esto resulta en varias propiedades que nos dan los logaritmos:
\log_{b}b = 1
\log_{b}b^{n} = n
b^{\log_{b}N} = N
Teorema 5
El logaritmo de un número positivo N en la base a, es igual al logaritmo de N en otra base b, dividido entre el logaritmo de a en la base b.
\log_{a}N = \frac{\log_{b}N}{\log_{b}a}
Ejemplos resueltos de logaritmos
Veamos unos ejemplos resueltos de logaritmos para que se logre entender mejor todos los conceptos anteriores.
Ejemplo 1 de logaritmos
Hallar el valor de x de la siguiente expresión:
\log_{b}x = \log_{b}2 + 3 \log_{b}2 - \log_{b}4
Para comenzar con este ejercicio de logaritmos, haremos que todos los logaritmos estén multiplicados por 1, a lo que me refiero es que al 3 del término 3\log_{b}2 lo podemos pasar como exponente del 2:
\log_{b}x = \log_{b}2 + \log_{b}2^{3} - \log_{b}4
Lo siguiente es que multiplicaremos los números de la suma de los logaritmos, tal y como lo dice nuestro teorema 1 de logaritmos:
\log_{b}x = \log_{b}2\cdot 2^{3} - \log_{b}4
En este paso podemos hacer dos cosas, ya sea multiplicar el 2 con el 2^{3} y luego aplicar el teorema 2 de los logaritmos o podemos primero aplicar el teorema 2 y luego multiplicar. Haremos lo que dijimos primero:
\log_{b}x = \log_{b}16 - \log_{b}4
\log_{b}x = \log_{b}\frac{16}{4} = \log_{b} 4
Y finalmente basándonos en una de nuestras propiedades del teorema 4 que dice:
b^{\log_{b}N} = N
Obtenemos nuestro resultado del valor de x:
b^{\log_{b}x}=x \ \ \text{y} \ \ b^{\log_{b}4} = 4
x = 4
Ejemplo 2 de logaritmos
Es este ejemplo utilizaremos logaritmos para hallar la función inversa de la siguiente función:
y = b^{x + 2}
Para comenzar con este ejercicio, lo que haremos es aplicar la propiedad siguiente de nuestro teorema 4:
\log_{b}b^{n} = n
Donde n es igual a x+2, así que aplicaremos logaritmo a toda la expresión:
\log_{b}y = \log_{b}b^{x+2}
Utilizaremos el teorema 3 para pasar el exponente de b multiplicando:
\log_{b}y = \left(x + 2 \right) \log_{b}b
Efectuamos unas operaciones sencillas:
\log_{b}y = x\log_{b}b + 2\log_{b}b
Ahora lo que haremos será pasar nuestra expresión 2\log_{b}b del otro lado de la igualdad
\log_{b}y - 2\log_{b}b = x\log_{b}b
Y ya casi terminamos, lo que aplicaremos ahora es una de nuestras propiedades de nuestro teorema 4 que dice:
\log_{b}b=1
Lo que nos hace poder eliminar el logaritmo donde está x y donde está el 2:
\log_{b}y - 2 = x
Ordenando la igualdad tenemos nuestro resultado de la función inversa hallada:
x = \log_{b}y - 2
Gracias por estar en este momento con nosotros : )
