En el análisis de regresión lo que se hace es relacionar una variable independiente con una variable dependiente, pero cuando ambas variables sean aleatorias no se debe de realizar un análisis de regresión, sino un análisis de correlación.
En el análisis de correlación no se desea hallar una relación lineal entre dos variables, sino que se intenta medir la intensidad de relación lineal entre X y Y.
Valores del coeficiente de correlación
Este parámetro del coeficiente de correlación asume valores entre -1 y 1, observa lo siguiente:
- Si r = 1, la correlación es perfecta positiva.
- Si r = -1, la correlación es perfecta negativa.
- Si r=0, no existe una correlación entre ambas variables.
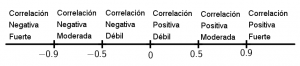
Se puede interpretar de la siguiente manera:
Fórmula para calcular el coeficiente de correlación
Hay una gran cantidad de cálculos para llegar a la fórmula del coeficiente de correlación, pero vamos a ahorrar todos esos cálculos y vamos directo con la fórmula:
r = \cfrac{n\sum xy - \sum x \sum y}{\sqrt{\left[ n\sum x^{2} - (\sum x)^{2}\right] \left[n \sum y^{2} - ( \sum y)^{2} \right]}}
Genial, ahora que ya tenemos la fórmula ¡vamos con el ejercicio!
Ejercicio del coeficiente de correlación
Veamos el enunciado del ejercicio:
En un estudio de movimiento de tierra ocasionados por sismos se registraron para cinco de éstos la velocidad máxima (en m/s) y la aceleración máxima (en m/s^{2}). Los resultados se presentan en la siguiente tabla:
\begin{array}{| c | c |}
\hline
\text{Velocidad} & \text{Aceleración} \\
\hline
1\text{.}54 & 7\text{.}64 \\
1\text{.}60 & 8\text{.}04 \\
0\text{.}95 & 8\text{.}04 \\
1\text{.}30 & 6\text{.}37 \\
2\text{.}92 & 5\text{.}00 \\
\hline
\end{array}- Calcula el coeficiente de correlación
- Alguien sugiere modificar las unidades a centímetros y minutos. ¿Qué efecto tendría en la correlación?
Inciso 1 del ejercicio
Excelente, vamos primero a calcular el coeficiente de correlación, para eso nos hace falta: \sum x, \sum y, \sum xy, \sum x^{2} y \sum y^{2}. Calculemos primero \sum x y \sum y:
\begin{array}{| c | c |}
\hline
\text{Velocidad} & \text{Aceleración} \\
\hline
1\text{.}54 & 7\text{.}64 \\
1\text{.}60 & 8\text{.}04 \\
0\text{.}95 & 8\text{.}04 \\
1\text{.}30 & 6\text{.}37 \\
2\text{.}92 & 5\text{.}00 \\
\hline
\sum x = 8\text{.}31 & \sum y = 35\text{.}09 \\
\hline
\end{array}Calculemos \sum xy:
\begin{array}{| c | c | c |}
\hline
\text{Velocidad} & \text{Aceleración} & xy \\
\hline
1\text{.}54 & 7\text{.}64 & 11\text{.}7656 \\
1\text{.}60 & 8\text{.}04 & 12\text{.}864 \\
0\text{.}95 & 8\text{.}04 & 7\text{.}638 \\
1\text{.}30 & 6\text{.}37 & 8\text{.}281 \\
2\text{.}92 & 5\text{.}00 & 14\text{.}6 \\
\hline
& & \sum xy = 55\text{.}1486 \\
\hline
\end{array}Ahora calculemos x^{2}:
\begin{array}{| c | c | c |}
\hline
\text{Velocidad} & \text{Aceleración} & x^{2} \\
\hline
1\text{.}54 & 7\text{.}64 & 2\text{.}3716 \\
1\text{.}60 & 8\text{.}04 & 2\text{.}56 \\
0\text{.}95 & 8\text{.}04 & 0\text{.}9025 \\
1\text{.}30 & 6\text{.}37 & 1\text{.}69 \\
2\text{.}92 & 5\text{.}00 & 8\text{.}5264 \\
\hline
& & \sum x^{2} = 16\text{.}0505 \\
\hline
\end{array}Ahora calculemos y^{2}:
\begin{array}{| c | c | c |}
\hline
\text{Velocidad} & \text{Aceleración} & y^{2} \\
\hline
1\text{.}54 & 7\text{.}64 & 58\text{.}3696 \\
1\text{.}60 & 8\text{.}04 & 64\text{.}6416 \\
0\text{.}95 & 8\text{.}04 & 64\text{.}6416 \\
1\text{.}30 & 6\text{.}37 & 40\text{.}5769 \\
2\text{.}92 & 5\text{.}00 & 25\text{.}00 \\
\hline
& & \sum y^{2} = 253\text{.}2297 \\
\hline
\end{array}Ahora sustituyamos directamente los valores en la fórmula:
r = \cfrac{(5)(55\text{.}1486) - (8\text{.}31)(35\text{.}09)}{\sqrt{\left[(5)(16\text{.}0505) - (8\text{.}31)^{2} \right] \left[(5)(253\text{.}2297) - (35\text{.}09)^{2} \right]}}
r = -0\text{.}8027
El coeficiente de correlación es r = -0\text{.}8027, por lo que indicó que es una correlación negativa moderada.
Inciso 2 del ejercicio
No tendría ningún efecto si cambiamos los valores a centímetros y minutos ya que sólo sería un cambio de unidades, o sea la correlación sería lo mismo, pero de todos modos vamos a comprobarlo. Calculemos primero \sum x y \sum y:
\begin{array}{| c | c |}
\hline
\text{Velocidad (cm/min)} & \text{Aceleración (cm/min}^{2}\text{)} \\
\hline
9240 & 45840 \\
9600 & 45840 \\
5700 & 48240 \\
7800 & 38220 \\
17520 & 30000 \\
\hline
\sum x = 49860 & \sum y = 210540 \\
\hline
\end{array}Ahora calculemos la sumatoria de x por y:
\begin{array}{| c | c | c |}
\hline
\text{Velocidad} & \text{Aceleración} & xy \\
\hline
9240 & 45840 & 423561600 \\
9600 & 45840 & 463104000 \\
5700 & 48240 & 274968000 \\
7800 & 38220 & 298116000 \\
17520 & 30000 & 525600000 \\
\hline
& & \sum xy = 1985349600 \\
\hline
\end{array}Ahora calculemos x^{2}:
\begin{array}{| c | c | c |}
\hline
\text{Velocidad} & \text{Aceleración} & x^{2} \\
\hline
9240 & 45840 & 85377600 \\
9600 & 45840 & 92160000 \\
5700 & 48240 & 32490000 \\
7800 & 38220 & 60840000 \\
17520 & 30000 & 306950400 \\
\hline
& & \sum x^{2} = 577818000 \\
\hline
\end{array}Ahora vamos a calcular y^{2}:
\begin{array}{| c | c | c |}
\hline
\text{Velocidad } & \text{Aceleración} & y^{2} \\
\hline
9240 & 45840 & 2101305600 \\
9600 & 45840 & 2327097600 \\
5700 & 48240 & 2327097600 \\
7800 & 38220 & 1460768400 \\
17520 & 30000 & 900000000 \\
\hline
& & \sum y^{2} = 9116269200 \\
\hline
\end{array}Ahora lo que vamos a hacer es colocar todos esos valores calculados en la fórmula para hallar el coeficiente de correlación:
r = \cfrac{(5)(1985349600) - (49860)(21054)}{\sqrt{\left[ (5)(577818000) - (49860)^{2}\right] \left[(5)(9116269200) - (210540)^{2} \right]}}
Utilizando una calculadora, obtendremos el siguiente valor:
r = -0\text{.}8027
¡Así que se puede comprobar que los coeficientes de correlación no cambian aunque tengan unidades diferentes, además quiere decir que sigue siendo una correlación negativa moderada!
Gracias por estar en este momento con nosotros : )