La estadística es el estudio que se encarga de la recolección, presentación, análisis y uso de datos para tomar decisiones, solucionar problemas y diseñar productos y procesos. (Montgomery, 2003)
Presentación de datos en la estadística
En la estadística existe la organización y la presentación gráfica de los datos. Los cuales la organización de datos son el uso de tablas y la presentación gráfica de los datos es precisamente el uso de gráficas como histogramas, polígonos, etc.
Primero vamos a tener un claro unos conceptos y seguidamente veremos un ejemplo:
Datos aislados
Este tipo de datos se enlistan pudiendo estar ordenados de alguna forma, ya sea ascendente, descendente o nula. Sólo es factible utilizarla cuando los datos son pocos y/o están separados entre sí ya que resulta muy confuso emplearla cuando la cantidad de datos es grande. Además este tipo de datos no requieren el uso de tablas.
Datos ordenados
Este tipo de datos implican el uso de tablas de frecuencia debido a que los datos se repiten frecuentemente y existe una cantidad grande y poco manejable. Sólo hay que contar el número de veces que se repite cada dato y apuntarlo en una columna de frecuencia.
Datos agrupados
En este caso, los datos se encuentran demasiado extendidos y/o no se repiten para que sea factible una tabla ordenada. Para ello se requiere crear intervalos en la tabla de un ancho adecuado y para determinar el rango de cada intervalo o clase se conviene utilizar la regla de Sturges.
Ejemplo de estadística
Agrupa los datos en una tabla y halla el polígono de frecuencias del siguiente ejemplo:
En su libro, Montgomery presentó información sobre la tasa de ahogamiento de niños entre 1 y 4 años por cada 100,000 habitantes en Arizona de 1970 a 2004. Los datos son: 19.9, 16.1, 19.5, 19.8, 21.3, 15.0, 15.5, 16.4, 18.2, 15.3, 15.6, 19.5, 14.0, 13.1, 10.5, 11.5, 12.9, 8.4, 9.2, 11.9, 5.8, 8.5, 7.1, 7.9, 8.0, 9.9, 8.5, 9.1, 9.7, 6.2, 7.2, 8.7, 5.8, 5.7 y 5.2.
Lo que haré es colocar los resultados y explicaré paso a paso cómo se obtuvo:
\begin{array}{|c|c|c|}
\hline
\text{Límites reales (Li)} & \text{Marca de clase} & \text{Frecuencia} \\
\hline
5.15 - 7.85 & 6.5 & 7 \\
7.85 - 10.55 & 9.2 & 11 \\
10.55 - 13.25 & 11.9 & 4 \\
13.25 - 15.95 & 14.6 & 5 \\
15.95 - 18.65 & 17.3 & 3 \\
18.65 - 21.35 & 20 & 5 \\
\hline
\end{array}¡Explicación del ejemplo anterior!
Podemos observar que los datos del ejemplo son agrupados, ¿por qué? Porque se encuentran demasiado extendidos y no es factible una tabla ordenada.
El límite real
Para los límites reales se necesita calcular el número de intervalos, el rango y el ancho de los datos.
Número de intervalos
Para el número de intervalos ( i ) se utiliza la regla de Sturges y se calcula con la fórmula es la siguiente:
i = 1 + 3.322 \log _{10}(n)
El cual n es el número de datos, en nuestro ejemplo el número de datos es de 35. Cuéntalos bien, parece que son 34 datos, pero en realidad son 35. Y como el número de intervalos tiene que ser un número entero, después de efectuar la fórmula, no importan los decimales que tenga, simplemente se truncarán.
i = 1 + 3.322 \log_{10}(35) \approx 6.1263 \rightarrow 6
Así que nuestro número de intervalos será de 6.
El rango
El rango simplemente es la resta del dato más grande menos el dato más pequeño, en nuestro ejemplo sería:
21.3\ - 5.2 = 16.1
16.1 sería el rango
El ancho
El ancho de calcula de la siguiente manera:
\text{Ancho} = \cfrac{\text{Rango}}{\text{Número de intervalos}}
En nuestro ejemplo el ancho sería de:
\text{Ancho} = \cfrac{16.1}{6} \approx 2.68 \rightarrow 2.7
El ancho siempre se redondea al siguiente valor, ¿pero cuál valor? En este caso los datos que nos ofrece el ejemplo cuentan con un decimal, así que al valor que se redondeará será al siguiente decimal, 2.68 se redondea a 2.7. Si en el ejemplo nuestros datos no tuvieran decimales y el ancho diera un número con decimales, redondearíamos al siguiente entero. ejemplo: 5.2 se redondea a 6. Si se llega a presentar el caso de que el ancho dio como resultado un número entero, se redondea al siguiente valor sí o sí, ejemplo: 5 se redondea a 6.
Uuuff, ahora sí…pasemos a la realización de la tabla para poder graficar el polígono de frecuencias.
Paso a paso, ¿cómo se realizan los intervalos?
Tengamos en cuenta la siguiente tabla:
\begin{array}{| c | c |}
\hline
\text{Número de decimales de el dato} & \text{Valor restado} \\
\hline
0 & 0.5 \\
1 & 0.05 \\
2 & 0.005 \\
\text{etc.} & \text{Siempre añadir un cero más.} \\
\hline
\end{array}Tomemos el dato más pequeño que ofrece el ejemplo y apliquemos la regla de la tabla anterior. Como el dato más pequeño es 5.2, entonces se le va a restar 0.05 porque 5.2 tiene sólo un decimal. El valor de nuestro límite real inferior en nuestro primer intervalo es 5.15 y el 7.85 que es el límite real superior se obtiene de la suma del 5.15 más el ancho:
5.15 + 2.7 = 7.85
Para la marca de clase lo que hay que hacer es sumar el límite real inferior más el límite real superior de ese intervalo y dividirlo entre 2:
\cfrac{5.15 + 7.85}{2} = 6.5
Y para determinar la frecuencia tienes que ponerte vivo para que no se te escape ningún dato, entonces cuentas los datos que están entre el intervalo de 5.15 y 7.85. La cantidad de datos que están en el primer intervalo es igual a 7 y son:
5.2, \ 5.7, \ 5.8, \ 5.8, \ 6.2, \ 7.1, \ 7.2
Nuestro primer intervalo queda de la siguiente manera:
\begin{array}{| c | c | c |}
\hline
\text{Li} & \text{Marca de clase} & \text{Frecuencia} \\
\hline
5.15\ - 7.85 & 6.5 & 7 \\
\hline
\end{array}Para colocar el siguiente intervalo se toma el límite real superior del intervalo anterior y se considera ahora como el límite real inferior del siguiente intervalo y se realiza el mismo proceso que se explicó en la marca de clase y en la frecuencia:
\begin{array}{| c | c | c |}
\hline
\text{Li} & \text{Marca de clase} & \text{Frecuencia} \\
\hline
5.15\ - 7.85 & 6.5 & 7 \\
7.85\ - 10.55 & 9.2 & 11 \\
\hline
\end{array}Y así sucesivamente hasta terminar de acompletar nuestros 6 intervalos
\begin{array}{| c | c | c |}
\hline
\text{Li} & \text{Marca de clase} & \text{Frecuencia} \\
\hline
5.15\ - 7.85 & 6.5 & 7 \\
7.85\ - 10.55 & 9.2 & 11 \\
10.55\ - 13.25 & 11.9 & 4 \\
13.25\ - 15.95 & 14.6 & 5 \\
15.95\ - 18.65 & 17.3 & 3 \\
18.65\ - 21.35 & 20 & 5 \\
\hline
\end{array}¡Ya tenemos la tabla, vayamos a la gráfica!
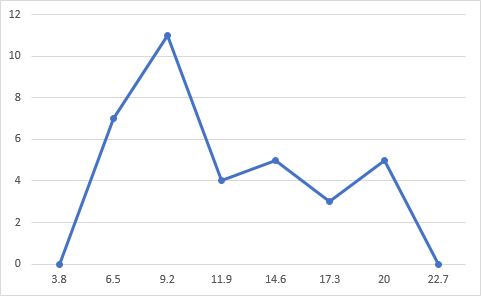
La manera correcta para trazar un polígono de frecuencia es considerar un par más de marcas de clase. A la marca de clase menor se le resta el ancho y a la marca de clase mayor se le suma el ancho y se considera como cero la frecuencia de las nuevas marcas de clase. Es por eso que tenemos el valor de 3.8 y 22.7 en el plano:
Y lo último es colocar la frecuencia de cada marca de clase y unir los puntos:
¡Y listo, ya sabes graficar polígonos de frecuencia!