Este tipo de datos son de los que más se utilizan en carreras como medicina, psicología, administración de empresas, etc. para llevar registros de inventarios, de personas y otro montón de cosas. La manera más sencilla de organizar un conjunto de datos es ordenarlos de menor a mayor y presentarlos en una tabla a la que le llamamos tabla de distribución de frecuencias. En esta tabla va asociada a cada dato un número que representa el número de veces que se repite un dato en el conjunto al que se le llama frecuencia (f) del dato. También veremos la representación gráfica, que es utilizando histogramas de frecuencia o polígonos de frecuencias.
Representación tabular de los datos ordenados
Primero, digamos que tenemos ciertos datos anotados en una libreta y lo que queremos hacer es tener una mejor organización con esos datos de unas calificaciones, los datos son los siguientes:
\begin{array}{c c c c c c c c c c}
8 & 9 & 6 & 7 & 5 & 7 & 8 & 5 & 9 & 10 \\
6 & 7 & 5 & 9 & 10 & 10 & 9 & 8 & 7 & 8 \\
9 & 9 & 8 & 9 & 6 & 5 & 10 & 10 & 7 & 7
\end{array}Para que se construya una tabla de distribución de frecuencias de forma ORDENADA para los 30 datos, se debe de contar el número de veces que se repiten los datos 5, 6, 7, 8, 9 y 10. Primero emplearemos marcas de cinco en cinco y luego escribiremos una columna más para colocar nuestra frecuencia (f) y la suma de todos los datos es la sumatoria de la frecuencia (\sum f).
\begin{array}{c l c} \text{Calificaciones} & \text{Conteo} & f \\ 5 & \boldsymbol{||||} & 4 \\ 6 & \boldsymbol{|||} & 3\\ 7 & \boldsymbol{\cancel{||||}} \ \boldsymbol{|} & 6\\ 8 & \boldsymbol{\cancel{||||}} & 5 \\ 9 & \boldsymbol{\cancel{||||}} \ \boldsymbol{||} & 7 \\10 & \boldsymbol{\cancel{||||}} & 5\\ & & \sum f = 30 \end{array}Otra forma de escribir los datos es de forma de frecuencia relativa (f_{r}), la cual se obtiene dividiendo la frecuencia de cada dato entre el total de datos o la sumatoria de la frecuencia. Así tenemos que la frecuencia relativa es el valor que representa la proporción del número de veces que se repite un dato en la colección.
\begin{array}{c | c | c} \text{Calificaciones} & f & f_{r}\\ \hline 5 & 4 & 13\text{.}33 \\ 6 & 3 & 10\text{.}00 \\ 7 & 6 & 20\text{.}00 \\ 8 & 5 & 16\text{.}66 \\ 9 & 7 & 23\text{.}33 \\ 10 & 5 & 16\text{.}66 \\ \hline & \sum f = 30 & \sum f_{r} = 100\text{.}00 \end{array}Y también tenemos otras dos formas de representar los datos en una tabla, una es la frecuencia acumulada (f_{a}) y la otra es la frecuencia acumulada relativa (f_{ar}):
\begin{array}{c | c | c | c } \text{Calificaciones} & f & f_{a} & f_{ar} \\ \hline 5 & 4 & 4 & 13\text{.}33 \\
6 & 3 & 7 & 23\text{.}33 \\ 7 & 6 & 13 & 43\text{.}33 \\ 8 & 5 & 18 & 60\text{.}00 \\ 9 & 7 & 25 & 83\text{.}33 \\ 10 & 5 & 30 & 100\text{.}00 \end{array}Representación gráfica de los datos ordenados
Histograma de frecuencias
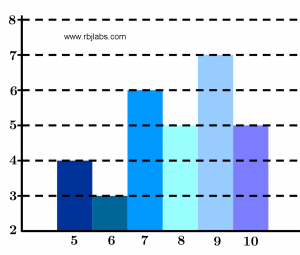
Un histograma de frecuencia es un gráfico que consiste en una serie de rectángulos que tienen sobre el eje horizontal sus bases de igual longitud y en el centro de cada rectángulo se colocan los datos y las alturas de cada rectángulo son las frecuencias correspondientes a los datos representados sobre el eje vertical.
En la Figura 1 puedes apreciar un ejemplo de un histograma de frecuencia donde se colocaron los datos mostrados anteriormente:
Polígono de frecuencias
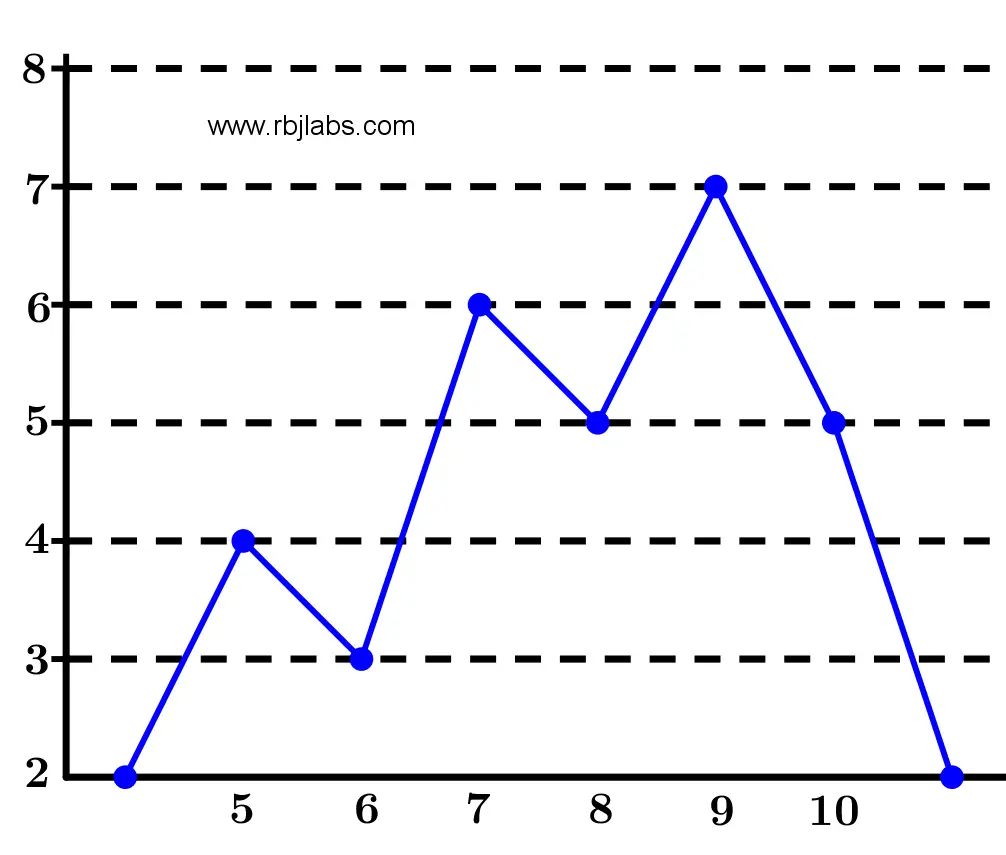
Esta gráfica es parecida al histograma de frecuencias, sólo que en vez de hacer rectángulos, se unen los puntos que representan cada dato. Se puede decir que es la unión de las partes más altas de cada uno de los rectángulos del histograma, sólo que para construir bien el polígono tenemos que empezar y terminar en el cero.
A continuación te presento en la Figura 2 un ejemplo del polígono de frecuencias utilizando los datos mencionados anteriormente:
Conclusión
La imaginación no tiene límites, tanto en el histograma como en el polígono se le pueden colocar en el eje vertical las frecuencias relativas, las frecuencias relativas porcentuales, las frecuencias acumuladas, la sumatoria de frecuencias, etc.
Estas gráficas no son nada más para colocar los datos y sus frecuencias, si bien es en lo que más se usa, pero tú puedes usarlas como se mencionó en el párrafo anterior.
Gracias por estar en este momento con nosotros : )
