Concepto de conjunto
Es una agrupación de personas, animales, u objetos dependiendo de sus características. Un conjunto podrían ser los perros, otro los gatos. Otro conjunto pueden ser los objetos de color azul. Las posibilidades son enormes para establecer conjuntos.
Definición de conjunto
Colección que tengan una característica en común, ya sea de personas, cosas, animales, ideas u objetos, llamados elementos. Como por ejemplo:
- Los días de la semana.
- Los meses del año.
- Los números primos.
- Los números pares.
Cardinalidad de un conjunto
Número de elementos que conforman a un conjunto y se denota N(\ ). Donde N es el conjunto y dentro del paréntesis va la cantidad de elementos que contiene ese conjunto. Los meses del año se representarían como:
A(12)Donde A representa al conjunto “Meses del año” y el número 12 es la cantidad de meses del año que hay.
Conjunto finito
Cuando es posible determinar el número exacto de elementos que tiene un conjunto. Como:
- Los días del mes de Enero.
- La cantidad de planetas de nuestro Sistema Solar.
Conjunto infinito
Cuando no es posible determinar el número exacto de elementos que tiene un conjunto. Como:
- Los números naturales.
- La cantidad de puntos en una línea.
Determinación de un conjunto según su expresión
Los conjuntos se pueden nombrar o escribir de las siguientes formas.
Conjuntos por extensión o enumerativa
Cuando se escriben de forma explícita sus elementos.
- A=\{\text{azul, blanco, rojo, amarillo} \}
- B=\{\text{pequeño, grande, mediano} \}
Conjuntos por comprensión
Cuando se describe la característica de los elementos que pertenecen al conjunto y hay qué establecer la relación de los objetos, cosas o personas que lo integran. Cuando nombramos un conjunto por comprensión, normalmente usamos simbologías. Algunas de ellas son las siguientes:
| Símbolo | Significado |
| \in | Pertenece |
| \notin | No pertenece |
| = | Igual a |
| \ne | Diferente |
| < | Menor que |
| > | Mayor que |
| \le | Menor o igual que |
| \ge | Mayor o igual que |
| | | Tal que o tales que |
| R | Número real |
| Q | Número racional |
| Z | Número entero |
Para trabajar los conjuntos por comprensión es necesario conocer el significado de ciertos símbolos matemáticos. Veamos el siguiente ejemplo:
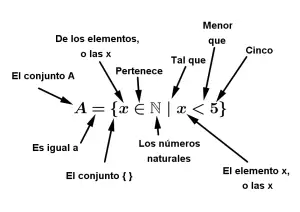
Así que A = \{ x\in \mathbb{N} \ | \ x < 5 \} se lee “El Conjunto A es igual al conjunto de todos los números que pertenecen a los números naturales, tal que, esos números sean menores que cinco“.
| Comprensión | Extensión | Lectura |
| A = \{ x\in \mathbb{Z} | x \ge 9 \} | A=\{ 9, 10, 11, \dots \} | El conjunto A es igual al conjunto de los números enteros tal que x sea mayor o igual a 9 |
| B = \{ x \in \mathbb{Z} | 1 < x < 6 \} | B = \{ 2, 3, 4, 5\} | El conjunto B es igual al conjunto de los números enteros tal que x sea mayor que 1 y menor que 6 |
Clases de conjuntos
Existen diferentes conjuntos de acuerdo con las características que estos presentan.
Conjunto universal
Se definen como la totalidad de elementos que poseen una características general común, denotada por el símbolo U. Un ejemplo puede ser:
- U = Los libros de la biblioteca.
- U = Las casas de tal ciudad.
Conjunto vacío o nulo
Es el conjunto que carece o tiene ningún elemento, representado como \varnothing.
- \varnothing = Las personas mayores de 400 años.
- \varnothing = Dinosaurios vivos existentes en la actualidad.
Conjuntos equivalentes
Dos conjuntos son equivalentes cuando los dos conjuntos poseen la misma cantidad de elementos y al mismo tiempo pueden establecer una correspondencia el uno del otro. Por ejemplo:
- Alumnos de un salón de clase.
- Sillas en un salón de clase.
Suponiendo que la cantidad de alumnos en un salón de clase es también la misma que las sillas en el mismo salón de clase.
Conjuntos iguales
Dos conjuntos son iguales, si y solo si, tienen los mismos elementos sin importar el orden en que estos se encuentren:
- A = \{ \text{a, e, i, o, u}\}
- B= \{ \text{i, u, a, o, e}\}
Subconjuntos
Un conjunto B es subconjunto de A si todos los elementos de B pertenecen a A. Si se cumple la condición, se dice entonces que B es subconjunto de A y se denota como B\subset A
- A = los alumnos de una escuela.
- B = los alumnos de la selección de fútbol de dicha escuela.
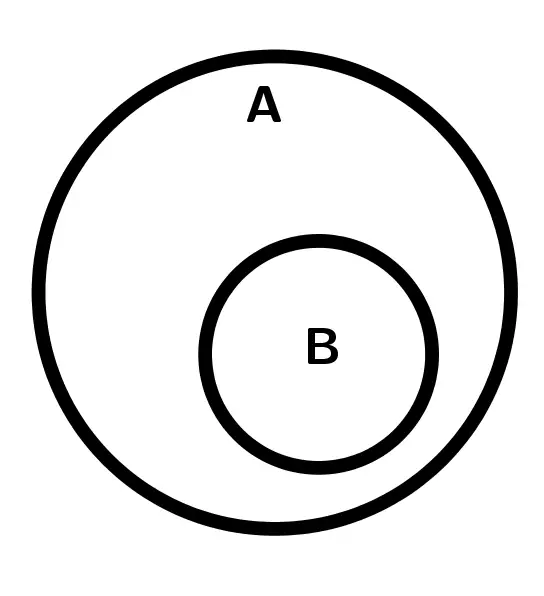 | 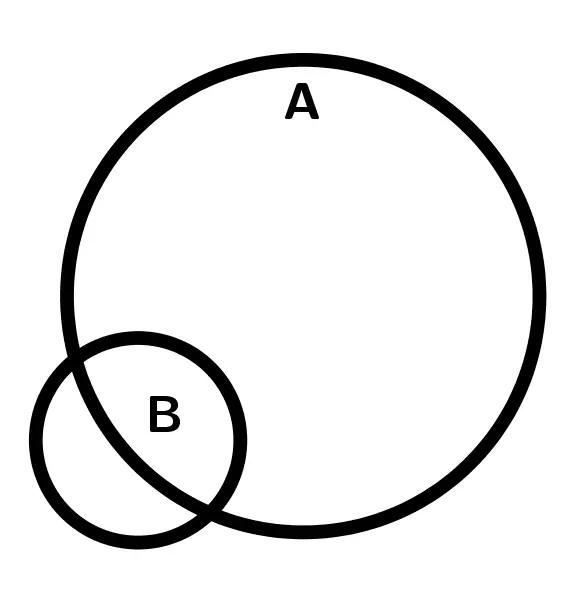 | 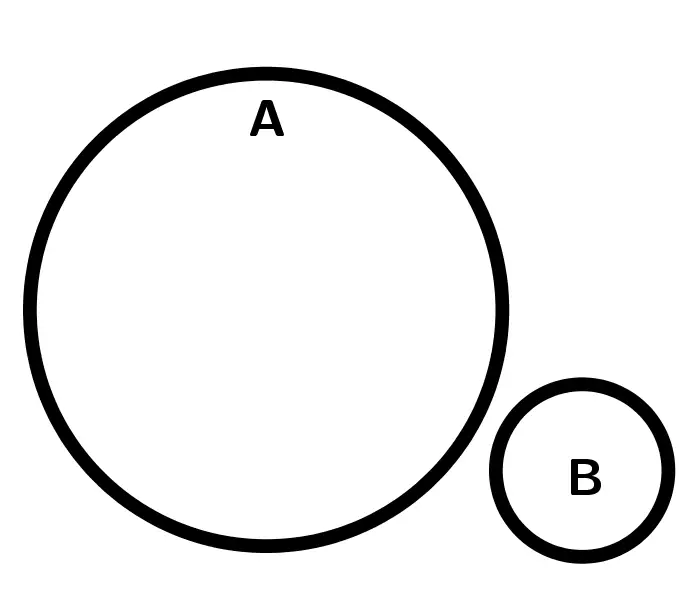 |
| B\subset A | B\not\subset A | B\not\subset A |
| A\not\subset B | A\not\subset B | A\not\subset B Son conjuntos distintos |
Diagrama de Venn-Euler
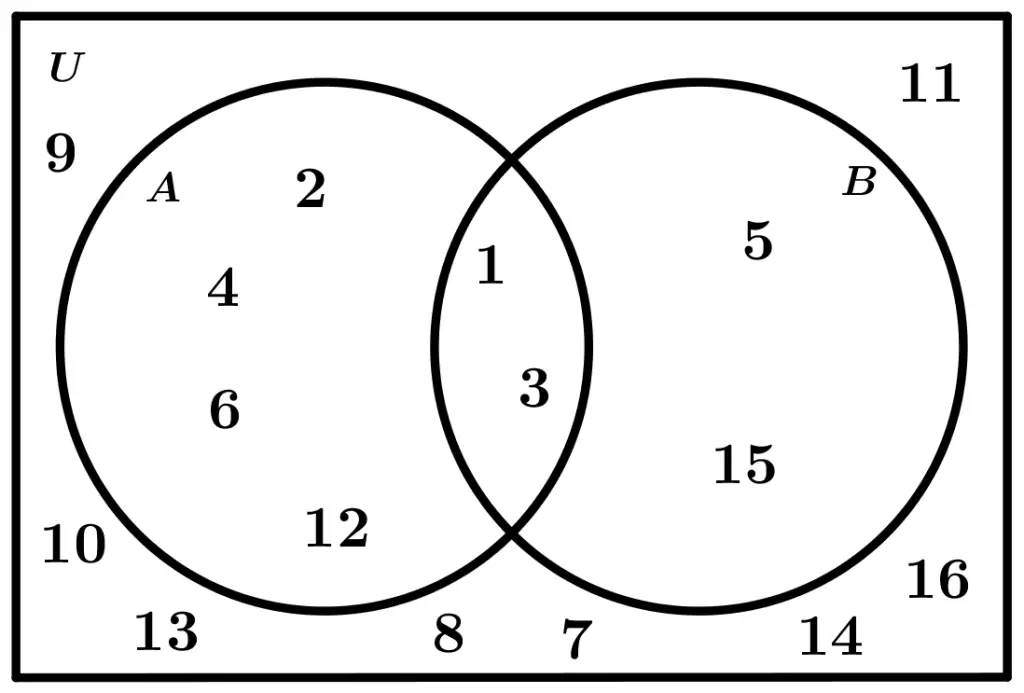
Tanto el conjunto A como el conjunto B están definidos únicamente por los elementos que se encuentran dentro de cada círculo. Es decir:
- A = \{ 1, 2, 3, 4, 6, 12\}
- B = \{ 1, 3, 5, 15\}
Mientras que el Universo U está constituido por todos los elementos que se encuentran en el rectángulo, es decir por todos los que están dentro y fuera de los círculos:
- U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16\}
Operaciones de conjuntos
Algunas de las operaciones que veremos como la unión, la intersección, la diferencia y el complemento se clasifican en binarias o singulares, tal y como se muestra en el siguiente ejemplo.
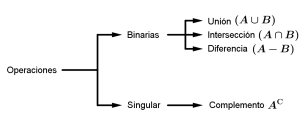
Unión de conjuntos
La unión de los conjuntos A y B, es el conjunto formado por todos los elementos de A y todos los elementos de B reunidos en uno solo y sin repetirlos. Si tienen elementos comunes, éstos sólo se escribirán una vez en el nuevo conjunto.
La notación que se emplea para esta operación es A\cup B y se define como:
A\cup B = \{ x / x \in A \ \text{ó} \ x \in B \}
Ejemplo de unión. Sean los conjuntos formados por:
A = \{ \text{Los divisores de } 12 \} = \{ 1, 2, 3, 4, 6, 12\}
B = \{ \text{Los divisores de } 15 \} = \{ 1, 3, 5, 15\}
U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16\}
Así que tenemos que la unión de A con B es:
A \cup B = \{ 1, 2, 3, 4, 5, 6, 12, 15\}
Intersección de conjuntos
La intersección de los conjuntos A y B es el conjunto que está integrado por los elementos comunes de los conjuntos dados.
La notación que lo representa es A \cap B y se define como:
A\cap B = \{ x / x \in A \ \text{y} \ x \in B\}
Utilizando los conjuntos A y B del ejemplo anterior, tenemos la intersección:
A\cap B = \{ 1, 3 \}
Diferencia de conjuntos
La diferencia de los conjuntos A y B es el nuevo conjunto que se forma con los elementos que pertenecen al conjunto A quitando los elementos que pertenecen al conjunto B o viceversa. La notación para esta operación es A-B o B-A y se define como:
A-B = \{ x / x \in A \ \text{ y } \ x \notin B \}
Utilizando los conjuntos A y B antes mencionados, la diferencia que se obtiene de A-B es:
A-B = \{ 2, 4, 6, 12 \}
Complemento del conjunto
El complemento de un conjunto A, es el conjunto formado por los elementos que pertenecen al universo U y no pertenecen al conjunto A.
La notación para esta operación ^{\text{C}} y se define como:
A^{\text{C}} = \{ x / x \in U \ \text{ y } \ x \notin A\}
Utilizando los conjuntos anteriores de A y B tenemos lo siguiente:
A = \{ 1, 2, 3, 4, 6, 12 \}
B = \{ 1, 3, 5, 15\}
U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 \}
Los complementos tanto del conjunto A como el conjunto B quedan de la siguiente forma:
A^{\text{C}} = \{ 5, 7, 8, 9, 10, 11, 13, 14, 15, 16\}
B^{\text{C}} = \{ 2, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16\}
Propiedades de los conjuntos
| Propiedad de identidad | A\cup \varnothing = A A \cup U = U A \cap U = A A \cap \varnothing = \varnothing |
| Propiedad de idempotencia | A \cup A = A A \cap A = A |
| Propiedad de complemento | A \cup A^{\text{C}} = U A \cap A^{\text{C}} = \varnothing |
| Propiedad asociativa | (A \cup B)\cup C = A \cup (B \cup C) (A \cap B) \cap C = A \cap (B \cap C) |
| Propiedad conmutativa | A \cup B = B \cup A A \cap B = B \cap A |
| Propiedad distributiva | A \cup (B \cap C) = (A \cup B) \cap (A \cup C) A \cap (B \cup C) = (A \cap B) \cup (A \cap C) |
Gracias por estar en este momento con nosotros : )
