Cómo saber si dos triángulos son semejantes
“Dos triángulos son semejantes si los ángulos homólogos son congruentes y los lados homólogos son proporcionales.” (Colonia, 2004, p. 289)
Nota: la “\Rightarrow” que se verán a continuación significan “entonces: “.
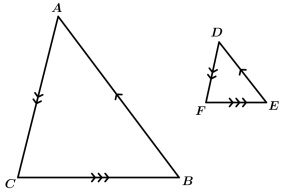
Postulado de la semejanza AAA (Ángulo-Ángulo-Ángulo)
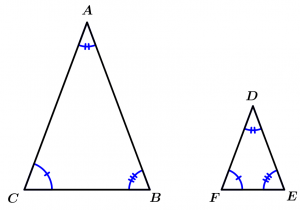
Si los 3 ángulos de un triángulo son congruentes con los 3 ángulos de otro triángulo, entonces los triángulos son semejantes.
\text{Si } \ \measuredangle A \cong \measuredangle D, \measuredangle B \cong \measuredangle E \ \land \ \measuredangle C \cong \measuredangle F
\Rightarrow \Delta ABC \sim \Delta DEF
Teoremas relativos a semejanzas de triángulos
Teorema 1. Semejanza AA (Ángulo-Ángulo)
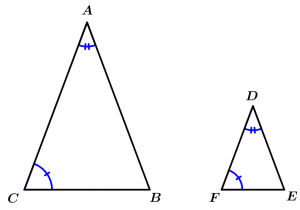
Si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos son semejantes.
\text{Si } \measuredangle A \cong \measuredangle D \ \land \ \measuredangle C \cong \measuredangle F
\Rightarrow \Delta ABC \ \sim \ \Delta DEF
Teorema 2. Semejanza LLL (Lado-Lado-Lado)
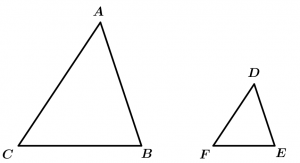
Si dos triángulos tienen proporcionales sus 3 lados, entonces los triángulos van a ser semejantes.
\text{Si } \ \cfrac{\overline{AB}}{\overline{DE}} = \cfrac{\overline{BC}}{\overline{EF}} = \cfrac{\overline{CA}}{\overline{FD}}
\Rightarrow \Delta ABC \ \sim \ \Delta DEF
Teorema 3. Semejanza LAL (Lado-Ángulo-Lado)
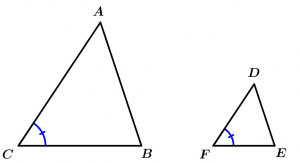
Si dos triángulos tienen dos lados proporcionales y los ángulos comprendidos entre dichos lados entonces son ángulos congruentes, entonces los triángulos son semejantes.
\text{Si } \ \cfrac{\overline{CA}}{\overline{FD}} = \cfrac{\overline{CB}}{\overline{FE}} \ \land \ \measuredangle C \cong \measuredangle F
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
Teorema 4
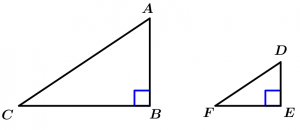
Si dos triángulos rectángulos tienen sus catetos proporcionales, entonces los triángulos son semejantes.
\text{Si } \measuredangle B \ \land \measuredangle E \ \text{ son rectos } \ \land
\cfrac{\overline{BA}}{\overline{ED}} = \cfrac{\overline{BC}}{\overline{EF}}
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
Teorema 5
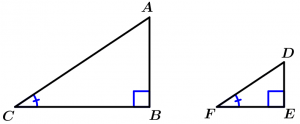
Si dos triángulos rectángulos tienen un ángulo agudo congruente, los triángulos son semejantes
\text{Si } \ \measuredangle B \ \land \ \measuredangle E \ \text{son rectos } \land
\measuredangle C \cong \measuredangle F
\Rightarrow \Delta ABC \ \sim \ \Delta DEF
Teorema 6
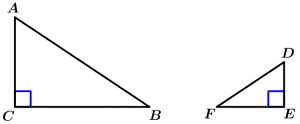
Si dos triángulos rectángulos tienen la hipotenusa y un cateto proporcionales, entonces los triángulos son semejantes.
\text{Si } \measuredangle C \ \land \measuredangle \ E \text{ son rectos } \ \land
\cfrac{\overline{AB}}{\overline{DF}} = \cfrac{\overline{AC}}{\overline{DE}}
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
Teorema 7
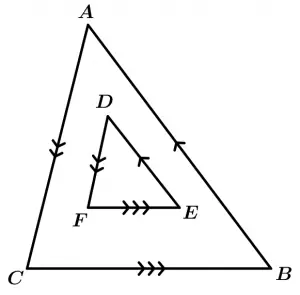
Si dos triángulos tienen sus lados correspondientes paralelos entre sí, son semejantes.
\text{Si } \overline{BA} \parallel \overline{ED}, \ \overline{AC} \parallel \overline{DF}, \ \overline{CB} \parallel \overline{FE}
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
No necesariamente tiene que estar un triángulo dentro de otro para identificar que tienen sus lados paralelos, pueden estar afuera uno de otro como se muestra a continuación:
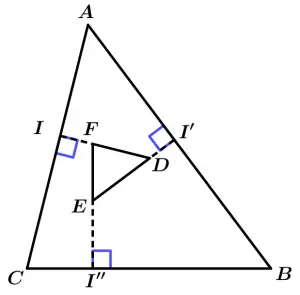
Teorema 8
Si cada lado de un triángulo es perpendicular con un lado correspondiente del segundo triángulo, entonces son triángulos semejantes.
\text{Si } \ \overline{DI} \bot \overline{AC}, \overline{EI'} \bot \overline{AB} \ \land \ \overline{FI''} \bot \overline{CB}
\Rightarrow \ \Delta ABC \ \sim \ \Delta DEF
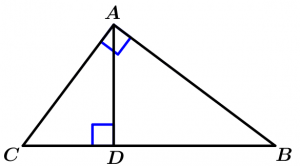
Teorema 9
La altura correspondiente divide al triángulo rectángulo dado en dos semejantes a éste y semejantes entre sí. Quiere decir que tenemos 3 triángulos semejantes. Además, la longitud de la altura correspondiente a la hipotenusa es la media proporcional entre las longitudes de los dos segmentos que divide la hipotenusa.
\text{Si } \Delta ABC \ \text{ es rectángulo siendo:}
\overline{CB} \ \text{ la hipotenusa } \ \land \ \overline{DA}
\text{la altura}
\Rightarrow \ \Delta ABC \ \sim \ \Delta ADC \ \sim \ \Delta ADB
\land \ \text{ la media proporcional es}
\Rightarrow \ \cfrac{\overline{CD}}{\overline{AD}} = \cfrac{\overline{AD}}{\overline{DB}}
Propiedades de las alturas de triángulos semejantes
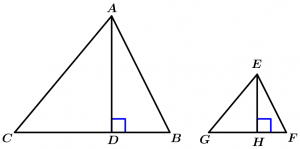
Teorema 10
Son proporcionales a los lados homólogos las alturas correspondientes de dos triángulos semejantes.
\text{Si } \Delta ABC \ \sim \ \Delta EFG \ \land
\overline{AD} \ \land \ \overline{EH} \ \text{ son alturas correspondientes}
\text{a los lados homólogos } \ \overline{CB} \ \land \ \overline{GF}
\Rightarrow \ \cfrac{AD}{EH} = \cfrac{CB}{GF}
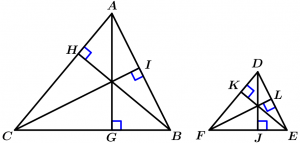
Teorema 11
Son proporcionales las alturas correspondientes de dos triángulos semejantes.
\text{Si } \Delta ABC \ \sim \ \Delta DEF \ \land
\overline{AG}, \overline{CI}, \overline{BH}, \overline{DJ}, \overline{FL} \ \land \ \overline{EK} \text{ son alturas}
\Rightarrow \cfrac{\overline{AG}}{\overline{DJ}} = \cfrac{\overline{CI}}{\overline{FL}} = \cfrac{\overline{BH}}{\overline{EK}}
Gracias por estar en este momento con nosotros : )