A continuación presentaremos las fórmulas básicas que utilizaremos para cálculos de energía en edificaciones, como corriente, voltaje, resistencia y potencia.
Fórmula de Ley de Ohm
Tenemos nuestra fórmula de Ley de Ohm, la cual es la más utilizada en los cálculos de circuitos eléctricos. Es la siguiente:
V=I\times R
La cual V es el voltaje o diferencia de potencial medida en volts (V); I es la corriente, intensidad o amperaje medida en amperes (A); R es la resistencia medida en ohms \Omega.
Primera fórmula de potencia
Tenemos que nuestra primera fórmula de potencia se parece mucho a la Ley de Ohm y es también muy fácil de recordar y aplicar. Dice así:
P=V \times I
Donde P es la potencia o el trabajo medida en watts W; y el voltaje y la corriente ya los vimos en la fórmula anterior a esta.
Segunda fórmula de potencia
Esta fórmula es muy útil cuando queremos calcular la potencia pero sólo tenemos la corriente y la resistencia:
P=I^{2} \times R
Y todas estas son variables que ya conocemos. De ahora en adelante ya no incluiremos variables desconocidas.
Tercera fórmula de potencia
Cuando tenemos sólo el voltaje y la resistencia, esta fórmula nos salva de todas esas ocasiones para determinar su potencia:
P = \cfrac{V^{2}}{R}
Fórmula de suma de resistencias
Recordando las fórmulas de las resistencias, tenemos dos, una es cuando se presentan resistencias en serie y la otra fórmula es cuando tenemos resistencias en paralelo. Es también a lo que conocemos como circuitos en serie y circuitos en paralelo.
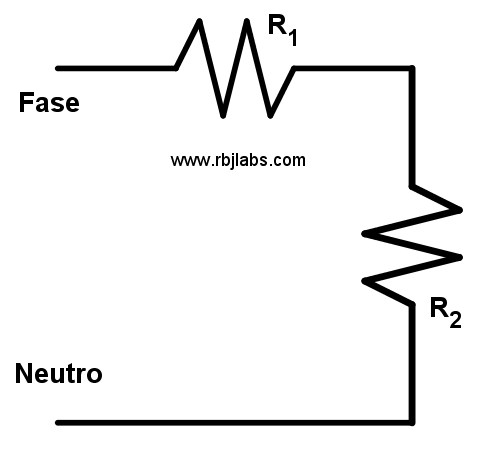 Resistencias en serie | 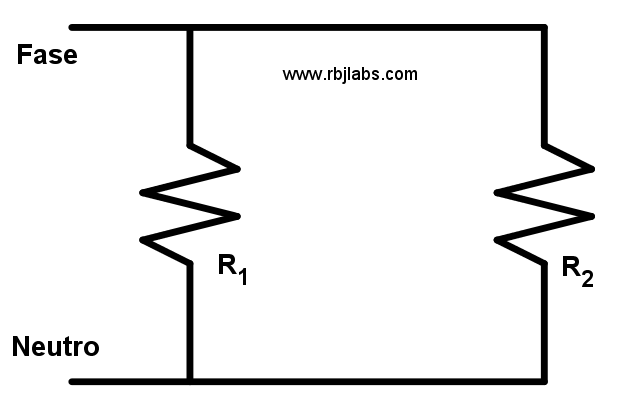 Resistencias en paralelo |
Fórmula de resistencias en serie
Esta fórmula es muy sencilla ya que lo único que hay que hacer es sumar, si tienes una resistencia con un valor y seguidamente tienes otra resistencia con el mismo u otro valor, se suman y listo, obtienes el valor de la resistencia total o resistencia equivalente R_{T}.
R_{T}=R_{1} + R_{2} + \dots + R_{n}
Fórmulas de suma de resistencias en paralelo
Esta fórmula es un poco más complicada ya que hay que tener cuidado a la hora de despejar la resistencia equivalente, ya que la fórmula es la siguiente:
\cfrac{1}{R_{T}} = \cfrac{1}{R_{1}} + \cfrac{1}{R_{2}} + \dots + \cfrac{1}{R_{n}}
Cuando tienes todas las sumas de los recíprocos de las resistencias tienes que despejar la R_{T} para obtener la resistencia total.
Gracias por estar en este momento con nosotros : )
