En este artículo explicaremos el cálculo del área entre un cardioide y una circunferencia utilizando integrales dobles, ¡comencemos!
Comenzaremos por escribir la función y la gráfica de nuestro cardioide y nuestra circunferencia.
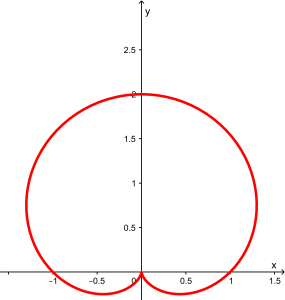
Nuestro cardioide tiene la siguiente gráfica y función:
r= 1+ \sin \theta
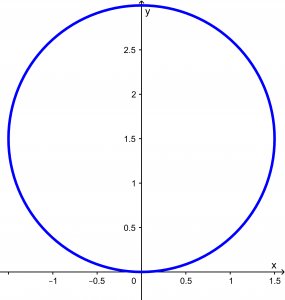
Y nuestra circunferencia tiene la siguiente función y gráfica:
3 \sin \theta
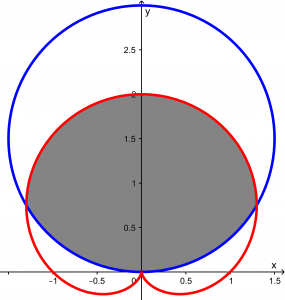
Ahora uniendo las dos gráficas, tendremos:
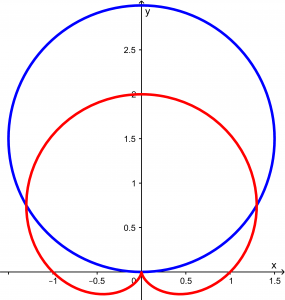
Y el área que queremos calcular es el área sombreada que se muestra en la siguiente figura:
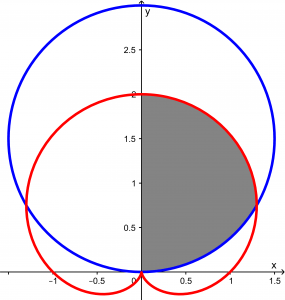
Observando la gráfica, se puede apreciar que es simétrica, así que para hacernos más fácil la vida, calcularemos sólo el área de la mitad y el resultado lo multiplicaremos por 2. Calcularemos esta área:
Observando las gráficas, lo que tendremos que hacer es una resolución de una suma de integrales dobles, ¿por qué? Porque primero vamos a calcular el área arriba y abajo del ángulo de intersección. Vamos a comenzar calculando el ángulo en el que se interceptan.
¿Pero cómo se calcula el ángulo en el que se interceptan? Fácil, vamos a igualar la función de la circunferencia con la función del cardioide, observa:
3\sin\theta = 1 + \sin \theta
Ahora lo que procedemos a realizar es la resolución de la igualdad para encontrar el ángulo \theta, así que pasamos restando el \sin \theta al 3\sin \theta:
3\sin \theta - \sin \theta = 1
2\sin \theta = 1
Ahora procedemos a pasar dividiendo el 2:
\sin \theta = \cfrac{1}{2}
Y finalmente para hallar \theta aplicamos seno inverso en ambos lados de la igualdad y lo que sucederá es que el seno que ya tenemos, se cancelará con el seno inverso y el \frac{1}{2} será \sin^{-1}\left(\frac{1}{2}\right):
\sin^{-1}\left(\sin \theta\right) = \sin^{-1}\left( \cfrac{1}{2}\right)
\theta = \sin^{-1} \left( \cfrac{1}{2}\right)
Podemos utilizar directamente la calculadora en el seno inverso en modo de radianes para determinar el valor de \theta, lo que nos da como resultado lo siguiente:
\theta = \cfrac{\pi}{6}
Excelente, ya tenemos el ángulo en radianes en el que se interceptan las dos funciones. Ahora podemos plantear nuestra suma de integrales dobles.
Plantearemos nuestra primera integral doble que está por debajo de \frac{\pi}{6}, eso quiere decir que el radio va a ser de cero a la función 3\sin\theta:
\displaystyle \int_{0}^{\frac{\pi}{6}} \int_{0}^{3\sin \theta}r \ dr \ d\theta
Ahora, nuestra segunda integral doble está arriba de \frac{\pi}{6}, eso quiere decir que el radio va a ser de cero a la función 1+\sin\theta, y además el ángulo de integración va a ser de \frac{\pi}{6} a \frac{\pi}{2}.
¿Pero por qué hasta \frac{\pi}{2}? Porque \frac{\pi}{2} significa que el ángulo va a ser hasta los 90°, que es la mitad del área que nosotros queremos calcular. Bueno, planteemos la segunda integral:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\int_{0}^{1 + \sin \theta}r \ dr \ d\theta
Bien, ya tenemos nuestras dos integrales planteadas, procederemos a resolver la primera integral de la primera integral doble.
Primera integral doble
\displaystyle \int_{0}^{\frac{\pi}{6}}\int_{0}^{3\sin \theta}r \ dr \ d\theta
Integrando tendremos como resultado lo siguiente:
\displaystyle \int_{0}^{\frac{\pi}{6}}\left.\cfrac{r^{2}}{2} \right|_{0}^{3\sin \theta} \ d \theta
Evaluamos:
\displaystyle \int_{0}^{\frac{\pi}{6}}\left(\cfrac{(3\sin \theta)^{2}}{2} - \cfrac{(0)^{2}}{2}\right) \ d \theta
\displaystyle \int_{0}^{\frac{\pi}{6}}\cfrac{9\sin^{2}\theta}{2} \ d \theta
Aplicando propiedades de la integrales sacaremos el \frac{9}{2} de la integral:
\displaystyle \cfrac{9}{2}\int_{0}^{\frac{\pi}{6}}\sin^{2}\theta \ d\theta
Para poder resolver la integral anterior, tenemos que aplicar la identidad trigonométrica siguiente:
\sin^{2}\theta = \cfrac{1}{2} - \cfrac{1}{2}\cos 2 \theta
Con lo cual nuestra integral quedaría de la siguiente manera:
\displaystyle \cfrac{9}{2}\int_{0}^{\frac{\pi}{6}} \left( \cfrac{1}{2} - \cfrac{1}{2} \cos 2\theta\right) d\theta
Ahora aplicando propiedad de integrales, separaremos la integral de una suma en una suma de integrales:
\displaystyle \cfrac{9}{2} \int_{0}^{\frac{\pi}{6}}\cfrac{1}{2} \ d\theta - \cfrac{9}{2} \int_{0}^{\frac{\pi}{6}} \cfrac{1}{2} \cos 2 \theta \ d \theta
Aplicando propiedades de integrales, sacaremos las fracciones de \frac{1}{2} de las integrales y multiplicaremos a las fracciones de \frac{9}{2}:
\displaystyle \cfrac{9}{4}\int_{0}^{\frac{\pi}{6}} \ d \theta - \cfrac{9}{4} \int_{0}^{\frac{\pi}{6}}\cos 2 \theta \ d \theta
¿Cómo resolver la integral de \cos 2 \theta \ d \theta? Tenemos que hacer un cambio de variable, vamos a ver cómo se hace. Llamaremos u a 2\theta, derivaremos y despejaremos:
u = 2 \theta
du = 2 d\theta
\cfrac{du}{2} = d\theta
Ahora sustituimos todas las variables que tengan \theta de la integral de \cos 2 \theta \ d \theta, quedaría de la siguiente manera:
\displaystyle \cfrac{9}{4}\int_{0}^{\frac{\pi}{6}} \ d\theta - \cfrac{9}{4} \int_{0}^{\frac{\pi}{6}} \cos u \cfrac{du}{2}
Integraremos de una vez la integral de la izquierda y aplicaremos propiedad de integrales en la integral de \cos u \ \cfrac{du}{2} para sacar el \frac{1}{2} de la integral y multiplicarlo con \frac{9}{4}:
\displaystyle \left.\cfrac{9}{4} \ \theta \right |_{0}^{\frac{\pi}{6}} - \cfrac{9}{8}\int_{0}^{\frac{\pi}{6}}\cos (u) \ du
Sustituiremos términos en \frac{9}{4} \theta y resolveremos la integral de \cos u \ du. Recordemos que la integral de \cos u es igual a \sin u:
\cfrac{9}{4}\left( \cfrac{\pi}{6} \right) - \cfrac{9}{4}(0) - \cfrac{9}{8} \left[ \left.\sin(u)\right|_{0}^{\frac{\pi}{6}} \right]
Multiplicaremos y sumaremos lo que se pueda resolver y sustituiremos de vuelta el u por el 2\theta:
\cfrac{9\pi}{24} - \cfrac{9}{8}\left[ \left. \sin(2\theta) \right|_{0}^{\frac{\pi}{6}} \right]
Ahora evaluaremos el \sin 2\theta, puedes ayudarte con una calculadora:
\cfrac{9\pi}{24} - \cfrac{9}{8}\left[ \sin\left(2\cfrac{\pi}{6}\right) - \sin(2(0))\right]=
\cfrac{9\pi}{24} - \cfrac{9}{8}\left[ \cfrac{\sqrt{3}}{2} - 0 \right]
Finalmente el resultado de nuestra primera integral doble será:
\cfrac{9\pi}{24} - \cfrac{9\sqrt{3}}{16}
Ahora procedamos con nuestra segunda integral doble
Tranquilo, que haciéndolo a mano y con práctica te podrás saltar muchos pasos, ¡animo!
Reescribamos nuestra segunda integral doble:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\int_{0}^{1 + \sin \theta}r \ dr \ d\theta
Resolviendo la integral de r\ dr, tendríamos lo siguiente:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left.\cfrac{r^{2}}{2}\right|_{0}^{1 + \sin \theta}\ d\theta
Evaluamos:
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left[\cfrac{(1 + \sin \theta)^{2}}{2} - \cfrac{(0)^{2}}{2}\right] \ d\theta
Resolveremos y tendremos como resultado lo siguiente
\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left[ \cfrac{(1 + \sin \theta)^{2}}{2}\right] \ d \theta
Aplicaremos propiedades de las integrales para sacar el \frac{1}{2} de la integral:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}(1 + \sin \theta)^{2} \ d \theta
Ahora efectuaremos el binomio al cuadrado:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left( 1 + 2 \sin \theta + \sin^{2} \theta \right) \ d \theta
Aplicando propiedades de las integrales, haremos que la integral de una suma, sea una suma de integrales:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \ d \theta + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} 2 \sin \theta \ d \theta + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \sin^{2} \theta \ d \theta
Aplicando más propiedades de integrales, sacaremos el 2 de la integral de 2\sin \theta \ d \theta para obtener lo siguiente:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \ d \theta + \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \sin \theta \ d \theta + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \sin^{2} \theta \ d \theta
La integral de d \theta y la integral de \sin \theta \ d \theta se resuelven muy fácil, vamos a resolverlas de una vez. Primero recordemos que la integral de \sin \theta es igual a -\cos \theta, ahora sí:
\displaystyle \cfrac{1}{2}\left[\left. \theta\right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\right] + \left[- \left. \cos \theta \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\right] + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\sin^{2}\theta d \theta
Ahora evaluamos:
\displaystyle \cfrac{1}{2} \left[ \cfrac{\pi}{2} - \cfrac{\pi}{6}\right] + \left[ -\cos\left( \frac{\pi}{2} \right)- \left(-\cos\left( \frac{\pi}{6} \right) \right)\right] + \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\sin^{2}\theta \ d \theta
Puedes ayudarte con una calculadora para resolver las evaluaciones del coseno y luego simplificas todo lo que se pueda simplificar:
\displaystyle \cfrac{1}{2} \left[ \cfrac{\pi}{3} \right] + \left[ 0 - \left(-\cfrac{\sqrt{3}}{2}\right)\right]+\cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\sin^{2}\theta \ d\theta =
\displaystyle \cfrac{\pi}{6} + \cfrac{\sqrt{3}}{2} + \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\sin^{2}\theta \ d\theta
Dejemos un checkpoint aquí.
Ahora sí, por el momento procedamos a resolver la integral de \sin^{2}\theta \ d \theta. Es sencillo resolverla, sólo tienes que saber la siguiente identidad trigonométrica:
\sin^{2} \theta = \cfrac{1}{2} - \cfrac{1}{2}\cos(2\theta)
Sustituyendo en la integral, quedaría de la siguiente manera:
\displaystyle \cfrac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\left( \cfrac{1}{2} - \cfrac{1}{2} \cos 2 \theta\right) \ d \theta
Aplicando propiedades de integrales, haremos que la integral de una suma sea la suma de las integrales:
\displaystyle \cfrac{1}{2} \int _{\frac{\pi}{6}}^{\frac{\pi}{2}}\cfrac{1}{2} \ d \theta + \cfrac{1}{2} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}-\cfrac{1}{2}\cos 2 \theta \ d \theta
Aplicando propiedades de integrales, sacaremos el signo negativo de la integral y además las fracciones de \frac{1}{2} y procederemos a multiplicarlas con las fracciones de \frac{1}{2} que ya teníamos:
\displaystyle \cfrac{1}{4} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\ d \theta - \cfrac{1}{4} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos 2 \theta \ d\theta
Para resolver la integral de \cos 2 \theta \ d \theta, se tiene que hacer un cambio de variable de u por 2\theta, derivar y despejar:
u = 2 \theta
du = 2 \ d \theta
\cfrac{du}{2} = d \theta
Ahora sí, sustituyamos todos los \theta que haya en la integral de coseno:
\displaystyle \cfrac{1}{4}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \ d \theta - \cfrac{1}{4} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos(u) \cfrac{du}{2}
Aplicando propiedades de integrales, sacaremos el \frac{1}{2} de la integral de coseno y lo multiplicaremos con el \frac{1}{4}:
\displaystyle \cfrac{1}{4}\int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \ d \theta - \cfrac{1}{8} \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos (u) \ du
Ahora fácilmente podemos resolver las dos integrales, recordemos que la integral de \cos u es igual a \sin u:
\cfrac{1}{4} \left[ \left. \theta \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}} \right] - \cfrac{1}{8}\left[ \left. \sin u \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\right]
Regresamos el cambio de variable de u a 2\theta:
\cfrac{1}{4} \left[ \left. \theta \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}} \right] - \cfrac{1}{8}\left[ \left. \sin 2\theta \right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}\right]
Puedes utilizar una calculadora para apoyarte en la evaluación de seno:
\cfrac{1}{4}\left[ \cfrac{\pi}{2} - \cfrac{\pi}{6}\right] - \cfrac{1}{8} \left[ \sin\left( \cfrac{2\pi}{2}\right) - \sin \left( \cfrac{2\pi}{6} \right)\right]=
\cfrac{1}{4}\left[ \cfrac{\pi}{3} \right]-\cfrac{1}{8} \left[ 0 - \cfrac{\sqrt{3}}{2}\right]
Multiplicamos lo que se pueda multiplicar y sumamos lo que se pueda sumar:
\cfrac{\pi}{12} + \cfrac{\sqrt{3}}{16}
Con el resultado obtenido, regresemos a nuestro checkpoint para sumar el resultado obtenido de las otras integrales:
\cfrac{\pi}{6} + \cfrac{\sqrt{3}}{2} + \cfrac{\pi}{12} + \cfrac{\sqrt{3}}{16}
Simplificando, obtendremos el siguiente resultado:
\cfrac{\pi}{4} + \cfrac{9\sqrt{3}}{16}
¡Al fin!
Ya que tenemos el resultado de nuestra primera integral doble y el resultado de nuestra segunda integral doble, procedemos simplemente a sumar los dos resultados:
\cfrac{9\pi}{24} - \cfrac{9\sqrt{3}}{16}+\cfrac{\pi}{4} + \cfrac{9\sqrt{3}}{16}
Resolvemos y nuestro resultado será:
\cfrac{5}{8} \pi
FINALMENTE
Ahora el resultado obtenido lo tenemos que multiplicar por 2 ya que sólo hallamos el área de la mitad de gráfica porque es simétrica, así que el resultado final es:
\cfrac{5}{4}\pi \ \text{u}^{2}
Gracias por estar en este momento con nosotros : )