¡Hola a todos!
El ejemplo que realizaremos a continuación es un tema muy bello de la materia de Cálculo que es la determinación del área de un cardioide dentro de una circunferencia. Recuerde que si va a utilizar la calculadora, tiene que colocarla en modo de radianes. Al final del artículo está el video de la explicación.
Gráfica de un cardioide
La ecuación de un cardioide r = 1 + \cos \theta se visualiza como se muestra a continuación:
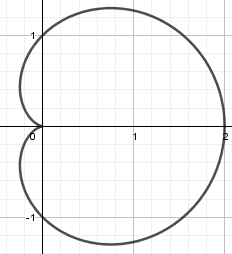
Gráfica de la circunferencia
La ecuación de la circunferencia r = 3 \cos \theta se visualiza como se muestra a continuación:
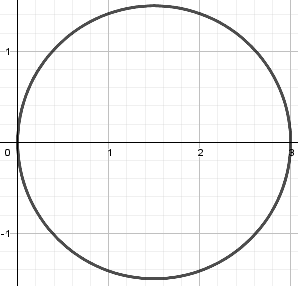
¿Entonces cuál es el área que estamos buscando?
El área es la que se limita por el cardioide y la circunferencia, la que se pinta de azul en la siguiente figura:
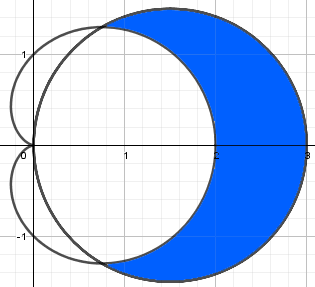
Resolvemos con integrales dobles
Para la resolución del ejercicio utilizaremos integrales dobles, la cual se representaría de la siguiente manera:
\displaystyle \int_{0}^{\frac{\pi}{3}} \int_{1 + \cos \theta}^{3 \cos \theta}r dr d\theta
Explicando cada parte de la integral:
Primera integral limitada por los radios de la circunferencia y el cardioide
La integral de r\ dr significa el radio, por lo tanto nosotros estamos integrando los radios, los cuales esos radios tienen un límite inferior de 1 + \cos \theta que corresponde al radio del cardioide y un radio superior de 3 \cos \theta que corresponde al radio de la circunferencia.
Segunda integral limitada por los puntos de intersección de la circunferencia y el cardioide
La segunda integral de d\ \theta es de qué a qué ángulo vamos a integrar, en este caso vamos a integrar del ángulo 0 al ángulo de 60 ° o \cfrac{\pi}{3} . ¿Que de dónde salió ese \cfrac{\pi}{3} ? Se explicará a continuación:
Igualamos las dos curvas que tenemos que son la del cardioide y la circunferencia para determinar el ángulo \theta :
1 + \cos \theta = 3 \cos \theta
Pasamos un \cos \theta de un lado para restarlo:
1 = 2 \cos \theta
Dividimos el 1 con el 2 :
\frac{1}{2} = \cos \theta
Aplicamos cos^{-1} a toda la igualdad:
\cos ^{-1}\left(\cfrac{1}{2}\right) = \theta
Y finalmente hallamos el ángulo de \theta , podemos usar la calculadora:
\theta = \frac{\pi}{3}
Y esa es la explicación por la cual los límites de integración van de 0 a \frac{\pi}{3} .
Nota:
El resultado que se obtenga al final se tendrá que multiplicar por 2 debido a que sólo se está hallando la parte de arriba del eje horizontal.
Realizamos todo el proceso de integración
\displaystyle \int_{0}^{\frac{\pi}{3}} \int_{1 + \cos \theta}^{3 \cos \theta}r dr d\theta
Integral de r
Integramos el r \ dr con sus respectivos límites y quedaría de la siguiente manera:
\left . \cfrac{r^{2}}{2} \right |_{1+ \cos \theta}^{3 \cos \theta}
Efectuamos la resta:
\cfrac{(3 \cos \theta)^{2} - (1 + \cos \theta)^{2}}{2}
Desglosamos el binomio al cuadrado perfecto:
\cfrac{9 \cos^{2} \theta \ - (1 + 2 \cos \theta + \cos^{2} \theta)}{2}
Simplificamos términos:
\cfrac{8 \cos^{2} \theta \ - 2 \cos \theta \ - 1}{2} = 4 \cos^{2}\theta \ - \cos \theta -\frac{1}{2}
Integral de \theta
Ahora la integral con respecto a \theta quedará de la siguiente manera:
\displaystyle \int_{0}^{\frac{\pi}{3}}(4 \cos^{2}\theta \ - \cos \theta \ -\frac{1}{2}) \ d\theta
Aplicando propiedades de la integrales, separamos las integrales para tener 3 integrales y que sea más sencillo integrar:
\displaystyle 4 \int_{0}^{\frac{\pi}{3}}cos^{2}\theta \ d\theta \ - \int_{0}^{\frac{\pi}{3}} \cos \theta \ d\theta \ - \frac{1}{2}\int_{0}^{\frac{\pi}{3}} \ d\theta
Para resolver la integral necesitamos saber una identidad trigonométrica muy poderosa que dice lo siguiente:
\cos^{2}\theta = \frac{1}{2}\cos 2 \theta + \frac{1}{2}
Y con esto resulta que ahora tendríamos 4 integrales:
\displaystyle 4 \int_{0}^{\frac{\pi}{3}} \frac{1}{2} \cos 2\theta \ d\theta + 4\int_{0}^{\frac{\pi}{3}}\frac{1}{2} \ d\theta \ - \int_{0}^{\frac{\pi}{3}} \cos \theta \ d\theta- \frac{1}{2}\int_{0}^{\frac{\pi}{3}} \ d\theta
Quiero que observemos \displaystyle 4 \int_{0}^{\cfrac{\pi}{3}} \cfrac{1}{2} \cos 2\theta \ d\theta
Vamos a reducir términos de esa integral:
\displaystyle 2 \int_{0}^{\frac{\pi}{3}} \cos 2\theta \ d\theta
Ahora vamos a realizar cambios de variable:
u = 2\theta
Derivamos:
du = 2 \ d\theta
Dejamos sola la d \ \theta :
\cfrac{du}{2} = d \theta
Y ahora la integral quedaría de la siguiente manera:
\displaystyle 2\int_{0}^{\frac{\pi}{3}} \cos u \frac{du}{2}
Cancelamos los 2 que aparecen:
\displaystyle \int_{0}^{\frac{\pi}{3}} \cos u \ du
Aplicamos la fórmula que dice:
\displaystyle \int \cos u \ du= \sin u \ du
Por lo tanto:
\displaystyle \int_{0}^{\frac{\pi}{3}} \cos u \ du = \left . \sin u \right |_{0}^{\frac{\pi}{3}}
Recordando que u = 2 \ \theta , quedaría como:
\left . \sin 2 \ \theta \right |_{0}^{\frac{\pi}{3}}
¡Reordenando todos los términos de la ecuación!
Reordenando todos los términos que hemos visto, quedaría de la siguiente manera:
\displaystyle \left . \sin 2 \theta \right |_{0}^{\frac{\pi}{3}} + 2 \int_{0}^{\frac{\pi}{3}} \ d\theta \ - \int_{0}^{\frac{\pi}{3}}\cos \theta \ d\theta \ - \frac{1}{2} \int_{0}^{\frac{\pi}{3}} \ d\theta
Recordando que \int \ d\theta = \theta , efectuaremos todas las integrales que faltan:
\left [ \sin 2 \theta + 2 \theta \ - \sin \theta \ - \frac{1}{2} \theta \right ]_{0}^{\frac{\pi}{3}}
Como todo va a ser evaluado de 0 a \frac{\pi}{3} , quedaría de la siguiente manera la expresión:
\sin (\frac{2\pi}{3}) + \frac{2\pi}{3} - \sin (\frac{\pi}{3}) - \frac{1}{2}(\frac{\pi}{3})
Podemos utilizar una calculadora e ingresar todos los valores y obtendremos lo siguiente:
\cfrac{\sqrt{3}}{2} + \cfrac{2\pi}{3} - \cfrac{\sqrt{3}}{2} - \cfrac{\pi}{6} = \cfrac{\pi}{2}
Pero recordemos que nosotros sólo hallamos la parte superior del eje de las abscisas, así que el resultado se tiene que multiplicar por 2.
Por lo tanto el resultado final del área del cardioide dentro de la circunferencia es igual a:
A = \pi u ^{2}
Video de la explicación:
Gracias por estar en este momento con nosotros : )
