Explicação simples do que é o diagrama de Venn. Operações básicas dos conjuntos representados com diagramas de Venn, exemplos de diagramas de Venn e, finalmente, vamos a ver fórmulas de contagem importantes! Algumas lousas muito boas já são utilizadas para realizar este tipo de exercícios de uma forma mais prática e visível.
O que é um Diagrama de Venn?
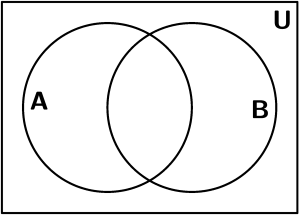
Simples, é a representação gráfica dos conjuntos.
A e B são quaisquer conjuntos
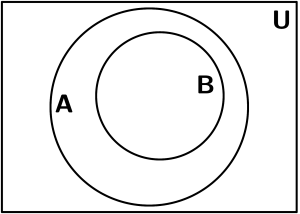
B é um subconjunto de A
Operações básicas dos conjuntos
União em Diagramas de Venn (\cup)
É o conjunto de todos os elementos que pertencem a A ou B. Quer dizer:
A \cup B = \{ x:x \in A\lor x \in B\}
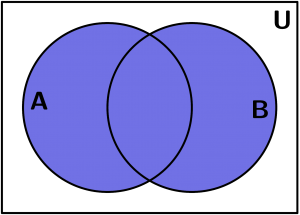
A \cup B
Intersecção em diagramas de Venn (\cap)
É o conjunto de elementos que pertencem a A e B. Isso significa que apenas a parte que os conjuntos compartilham é desenhada:
A \cap B = \{ x:x \in A \land x \in B\}
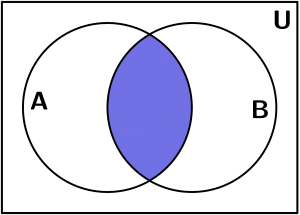
A \cap B
Complemento de um conjunto (^{\text{C}})
É o conjunto de elementos que pertencem ao universo que não faz parte de A. Em outras palavras:
A^{\text{C}} = \{ x:x\in U, x \notin A\}

A^{\text{C}}
Diferença nos diagramas de Venn (-)
É o conjunto gerado removendo os elementos presentes no segundo conjunto:
A- B = \{ x:x \in A, x \notin B\}
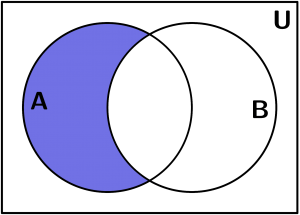
A- B
Exemplo de conjuntos com diagramas de Venn
Suponha que o Universo seja definido da seguinte forma:
U = \{ 1,2,3,4,5,6,7,8,9,10\}
E os seguintes conjuntos são delimitados:
A = \{ 1,2,3,4\}, \ B = \{ 3,4,5,6,7\}, \ C = \{ 2,3, 8,9\}
O diagrama de Venn é representado da seguinte forma:
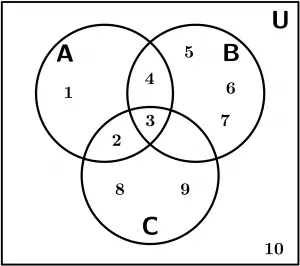
Perfeito, vamos começar com os exemplos do Diagrama de Venn
Primeiro Exemplo de Diagrama de Venn
Faça a união do conjunto A com o conjunto B e a união do conjunto B com o conjunto C:
A \cup B \cup C
Fazendo o acima, os números que teríamos são os seguintes:
\{ 1,2,3,4,5,6,7,8,9\}
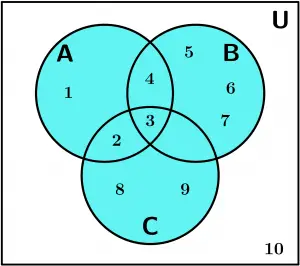
A \cup B \cup C
Segundo exemplo de diagrama de Venn
Faça a interseção do conjunto A com o conjunto B e a interseção do conjunto B com o conjunto C:
A \cap B \cap C
Fazendo o que foi dito acima, o número que resta é apenas um, pois é o que os três conjuntos têm em comum:
\{ 3\}
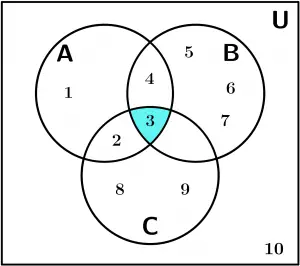
A \cap B \cap C
Terceiro Exemplo de Diagrama de Venn
Completa o conjunto A menos a interseção do conjunto B com o conjunto C:
A^{\text{C}} - (B \cap C)
É importante seguir as etapas em ordem:
1. Os parênteses são priorizados, então B \cap C é feito primeiro:
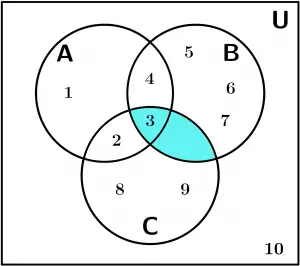
B \cap C
2. Observamos o complemento de A :
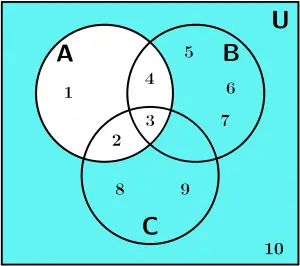
A^{\text{C}}
3. Finalmente fazer a diferença A^{\text{C}} - (B \cap C)
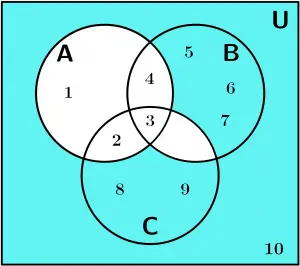
A^{\text{C}} - (B \cap C)
Resultado:
\{ 5,6,7,8,9,10\}
Fórmulas de contagem do diagrama de Venn
Se n(A), n(B) e n(C) são o número de elementos que compõem os conjuntos A, B e C respectivamente, então as fórmulas do diagrama de Venn são:
- n(A \cup B) = n(A) + n(B) - n(A \cap B)
- n(A - B)=n(A) - n(A \cap B)
- n(A^{\text{C}}) = n(U) - n(A)
- n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(A \cap C) - n(B \cap C) + n(A \cap B \cap C)
Obrigado por estar connosco neste momento : )