Com os estudos na escola, é altamente recomendável que você tenha um bom conjunto de geometria para que todas as suas figuras saiam perfeitas.
Definição de linhas paralelas
Duas linhas são paralelas se não se cruzarem, não importa quanto durem. Então veremos na imagem a seguir exemplos de paralela, oblíqua e perpendicular.
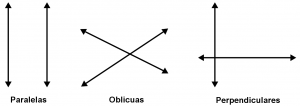
Quando duas linhas se cruzam, independentemente da medida dos ângulos formados nelas, elas são linhas oblíquas. Também é conhecido como linhas secantes.
Quando duas linhas se cruzam e formam ângulos de 90 graus entre elas, são consideradas linhas oblíquas e linhas perpendiculares. Como bem se diz: toda linha perpendicular é oblíqua, mas nem toda linha oblíqua é perpendicular. É assim que dizemos que cada linha é perpendicular secante. Vamos continuar falando sobre linhas paralelas e perpendiculares e linhas que são interseccionadas por uma que não é perpendicular.
Propriedades de linhas paralelas
As 3 propriedades das linhas paralelas são as seguintes:
As linhas paralelas são simétricas ou recíprocas
Esta propriedade diz que se uma linha a é paralela a uma linha b, então a linha b é paralela à linha a.
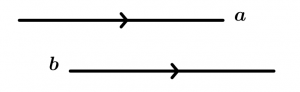
\text{Se } \ a \parallel b \ \text{ então } \ b \parallel a
Linhas paralelas são transitivas
Se uma linha a é paralela a uma linha b e a linha b é paralela a uma linha c, então a linha c é paralela à linha a.
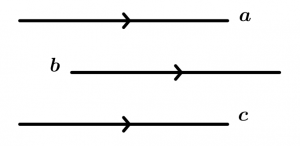
\text{Se } \ a \parallel b \ \text{ e } \ b \parallel c \ \text{ então } \ c \parallel a
Idêntico ou reflexivo
Essa propriedade nos diz que cada linha é paralela a se mesma.

a \parallel a
Postulados de linhas paralelas
Postulado de Euclides (dos paralelos)
Para um ponto Q fora de uma linha a passa um e apenas um paralelo a essa linha.
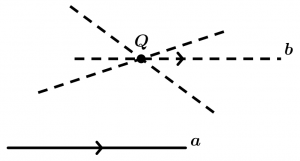
Este postulado significa que apenas uma linha paralela passará pelo ponto Q, não mais do que duas linhas paralelas podem passar pelo ponto Q.
Postulado de linhas cortadas por uma secante ou transversal
Se duas linhas a e b são cortadas por uma linha transversal t e um par de ângulos correspondentes são congruentes, então as linhas a e b são paralelas.
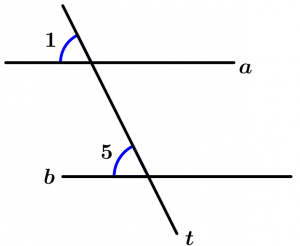
\text{Se } \ \measuredangle 1 \cong \measuredangle 5
\text{então } \ a \parallel b
Todas as linhas t que cruzam linhas paralelas são consideradas linhas transversais. Agora podemos dizer que são linhas paralelas cortadas por uma secante.
Teoremas de linhas paralelas
Nos trabalhos escolares, é altamente recomendável que você tenha um jogo de geometria para que as linhas fiquem perfeitas.
Teorema 1
Se duas linhas a e b são perpendiculares a uma linha t, então a e b são paralelas.
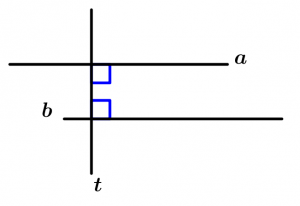
\text{Se } \ a \bot t \ \text{ e } \ b \bot t
\text{então } \ a \parallel b
A linha a é uma linha paralela e perpendicular, assim como a linha b.
Teorema 2
Se uma linha t corta outra, também corta qualquer linha paralela a ela.
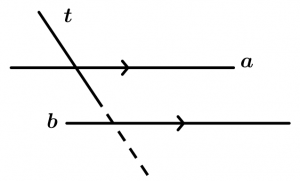
Teorema 3
Qualquer linha perpendicular a uma linha é perpendicular a qualquer linha paralela a ela.
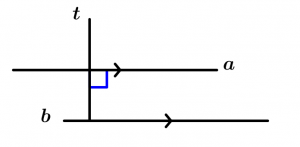
\text{Se } \ a \parallel b \ \text{ e } \ a \bot t
\text{então } \ b \bot t
Antes de continuar com os teoremas das linhas paralelas
Antes de continuar com os teoremas, temos que esclarecer alguns conceitos, eles são simples, mas necessários. Veremos ângulos internos, ângulos externos, ângulos correspondentes, ângulos internos alternados, ângulos internos conjugados e ângulos externos conjugados. Vamos aos exemplos.
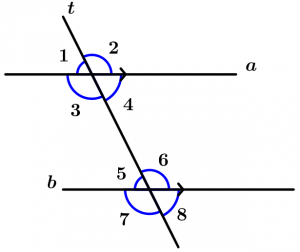
Ângulos internos
São aqueles ângulos que estão entre as duas linhas que são cortadas pela linha transversal, esses ângulos são 3, 4, 5 e 6.
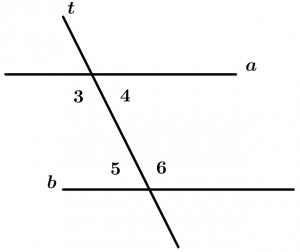
\measuredangle 3, \measuredangle 4, \measuredangle 5 \ \text{ e } \ \measuredangle 6
\text{são ângulos internos}
Ângulos externos
São aqueles ângulos que não estão entre as duas linhas e que são cortados pela linha transversal, esses ângulos são 1, 2, 7 e 8.
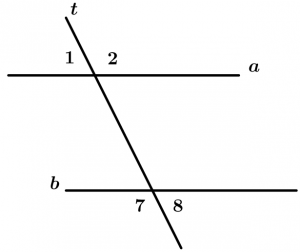
\measuredangle 1, \measuredangle 2, \measuredangle 7 \ \text{ e } \ \measuredangle 8
\text{são ângulos externos}
Ângulos correspondentes
São todos aqueles ângulos que estão localizados no mesmo lado da transversal, um é interno e o outro é externo, eles estão agrupados em pares que são 4.
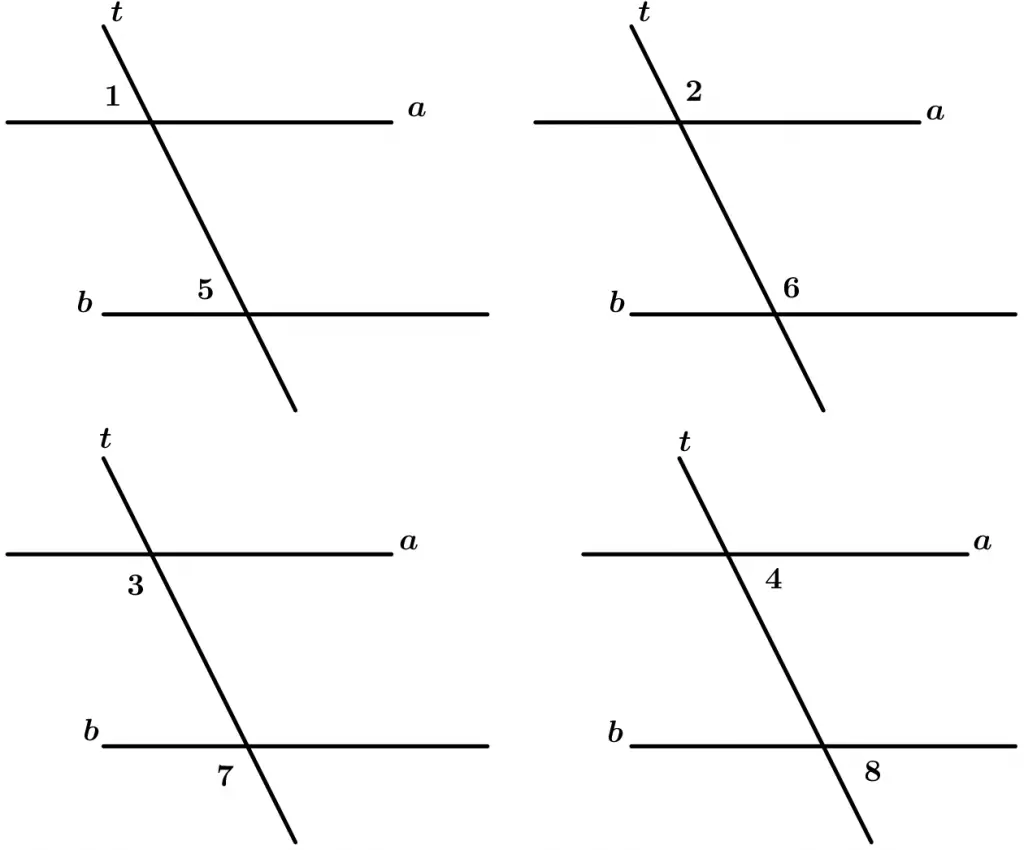
Os pares de ângulos correspondentes são:
\text{Par 1: } \ \measuredangle 1 \text{ e }\measuredangle 5
\text{Par 2: } \ \measuredangle 2 \text{ e }\measuredangle 6
\text{Par 3: } \ \measuredangle 3 \text{ e }\measuredangle 7
\text{Par 4: } \ \measuredangle 4 \text{ e }\measuredangle 8
Ângulos internos alternativos
São dois ângulos internos com vértices diferentes e que estão em lados diferentes da transversal, estão agrupados aos pares e são 2.
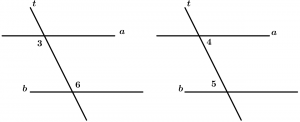
Pares de ângulos internos alternados:
\text{Par 1: } \ \measuredangle 3 \text{ e }\measuredangle 6
\text{Par 2: } \ \measuredangle 4 \text{ e }\measuredangle 5
Ângulos externos alternativos
São dois ângulos exteriores com vértices diferentes e que estão em lados diferentes da transversal, estão agrupados aos pares e são 2.
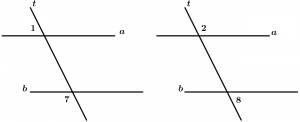
Pares de ângulos externos alternativos:
\text{Par 1: } \ \measuredangle 1 \text{ e }\measuredangle 8
\text{Par 2: } \ \measuredangle 2 \text{ e }\measuredangle 7
Ângulos conjugados internos
São dois ângulos internos com vértices diferentes e que estão do mesmo lado da transversal, estão agrupados aos pares e são 2.
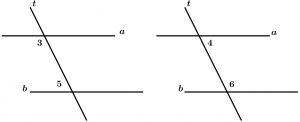
Pares de ângulos internos conjugados:
\text{Par 1: } \ \measuredangle 3 \text{ e }\measuredangle 5
\text{Par 2: } \ \measuredangle 4 \text{ e }\measuredangle 6
Ângulos externos conjugados
São dois ângulos externos com vértices diferentes e que estão do mesmo lado da transversal, estão agrupados aos pares e são 2.

Pares de ângulos exteriores conjugados:
\text{Par 1: } \ \measuredangle 1 \text{ e }\measuredangle 7
\text{Par 2: } \ \measuredangle 2 \text{ e }\measuredangle 8
Teorema 4
Se uma linha a e b são cortadas por uma linha transversal t e acontece que um par de ângulos internos alternados são congruentes, então as linhas a e b são paralelas.
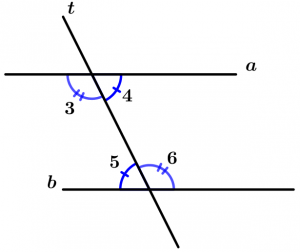
\text{Se uma declaração diz que } \ \measuredangle 3 \cong \measuredangle 6
\text{ou que } \ \measuredangle 4 \cong \measuredangle 5
\text{então } \ a\parallel b
Teorema 5. O teorema PAI
Se duas linhas paralelas a e b são interceptadas por uma linha transversal t, então os ângulos internos alternativos são congruentes.
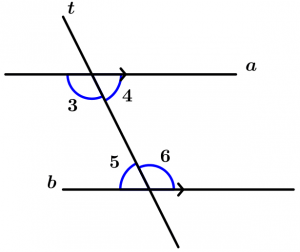
\text{Se } \ t \ \text{ corte para os paralelos } \ a \ \text{ e } \ b
\text{então } \ \measuredangle 3\cong \measuredangle 6 \ \text{ e } \ \measuredangle 4 \cong \measuredangle 5
Teorema 6
Qualquer linha transversal t se forma com duas linhas paralelas a e b, ângulos externos alternados congruentes.
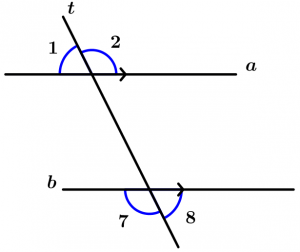
\text{Se } \ t \ \text{ cortar as linhas paralelas} \ a \ \text{ e } \ b
\text{então } \ \measuredangle 1 \cong \measuredangle 8 \ \text{ e } \ \measuredangle 2 \cong \measuredangle 7
Teorema 7
Se duas linhas a e b são interseccionadas por uma linha transversal t e um par de ângulos externos alternativos são congruentes, então as linhas a e b são paralelas.
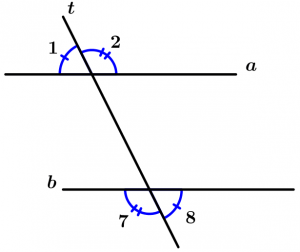
\text{Se } \ a \ \text{ e } \ b \ \text{ são cortados por } \ t
\text{ e a declaração diz que } \ \measuredangle 1 \cong \measuredangle 8 \text{ ou que }
\measuredangle 2 \cong \measuredangle 7 \ \text{ então}
a \parallel b
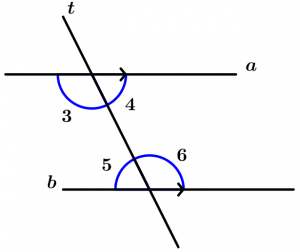
Teorema 8
Cada linha transversal t se forma com duas linhas paralelas a e b ângulos congruentes correspondentes.
Pares de ángulos correspondientes congruentes:
\text{Par 1: } \ \measuredangle 1 \text{ e }\measuredangle 5
\text{Par 2: } \ \measuredangle 2 \text{ e }\measuredangle 6
\text{Par 3: } \ \measuredangle 3 \text{ e }\measuredangle 7
\text{Par 4: } \ \measuredangle 4 \text{ e }\measuredangle 8
Teorema 9
Se duas linhas paralelas a e b são cortadas por uma linha transversal t, então os ângulos internos conjugados são complementares.
\text{Se as linhas paralelas} \ a \ \text{ e } \ b
\text{são cortados por } \ t, \ \text{ então}
\measuredangle 3 + \measuredangle 5 = 180^{\text{o}} \ \text{ e}
\measuredangle 4 + \measuredangle 6 = 180^{\text{o}}
Teorema 10
Se duas linhas a e b são interseccionadas por uma linha transversal t e os ângulos internos conjugados são suplementares, então as linhas a e b são paralelas.
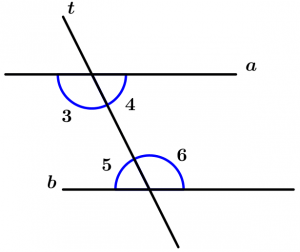
\text{Se as linhas } \ a \ \text{ e } \ b \ \text{são cortados por }
t \ \text{ e a declaração diz que:}
\measuredangle 3 + \measuredangle 5 = 180^{\text{o}} \ \text{ ou que}
\measuredangle 4 + \measuredangle 6 = 180^{\text{o}}
\text{então } \ a \parallel b
Teorema 11
Se duas linhas paralelas a e b são cortadas por uma linha transversal t, então os ângulos exteriores conjugados são suplementares.
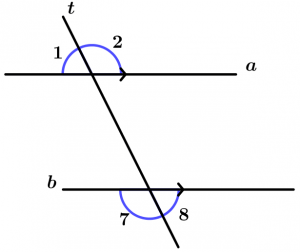
\text{Se as linhas paralelas} \ a \ \text{ e } \ b
\text{são cortados por } \ t, \ \text{ então}
\measuredangle 1 + \measuredangle 7 = 180^{\text{o}} \ \text{ e}
\measuredangle 2 + \measuredangle 8 = 180^{\text{o}}
Teorema 12
Se duas linhas a e b são interseccionadas por uma linha transversal t e os ângulos externos conjugados são suplementares, as linhas a e b são paralelas.
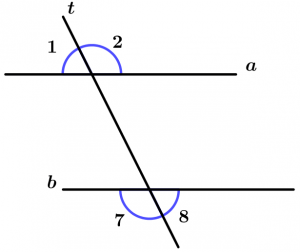
\text{Se as linhas } \ a \ \text{ e } \ b \ \text{são cortados por }
t \ \text{ e a declaração diz que:}
\measuredangle 1 + \measuredangle 7 = 180^{\text{o}} \ \text{ ou que}
\measuredangle 2 + \measuredangle 8 = 180^{\text{o}}
\text{então } \ a \parallel b
Teorema 13
Se dois ângulos têm seus lados respectivamente paralelos, esses ângulos são congruentes ou complementares.
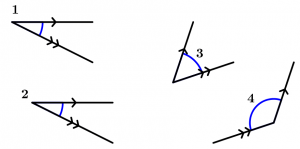
\measuredangle 1 \cong \measuredangle 2
\measuredangle 3 + \measuredangle 4 = 180^{\text{o}}
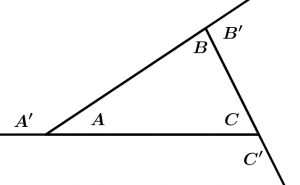
Teorema 14, 15, 16
14. A soma das medidas dos ângulos internos de um triângulo é igual a 180 °.
\measuredangle A + \measuredangle B + \measuredangle C = 180^{\text{o}}
15. A soma das medidas dos ângulos externos de um triângulo é igual a 360 °.
\measuredangle A' + \measuredangle B' + \measuredangle C' = 360^{\text{o}}
16. A medida de cada ângulo externo em um triângulo é igual à soma das medidas dos dois ângulos internos não adjacentes.
\measuredangle A' = \measuredangle B + \measuredangle C
\measuredangle B' = \measuredangle A + \measuredangle C
\measuredangle C' = \measuredangle A + \measuredangle B
Lembre-se de que aqui você pode obter um jogo de geometria para aplicar perfeitamente os teoremas.
Obrigado por estar conosco neste momento : )
