Classificação de triângulos de acordo com seus lados
Triângulo equilátero
Os triângulos equilaterais são aqueles que têm três lados iguais e, por terem três lados iguais, também têm três ângulos iguais.
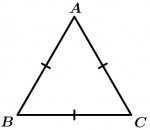
O \Delta ABC é equilátero.
\overline{AB} = \overline{BC} = \overline{AC}
Triângulo isósceles
Triângulos isósceles são aqueles que possuem apenas dois de seus lados iguais.
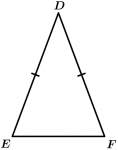
O \Delta DEF é isósceles.
\overline{ED} = \overline{DF}
Por ter dois de seus lados iguais, ele também tem dois de seus ângulos iguais. O ângulo oposto do lado DF é igual ao ângulo oposto do lado DE :
\measuredangle E = \measuredangle F
Triângulo escaleno
Os triângulos escalenos são aqueles que possuem seus três lados desiguais.
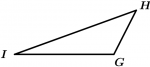
O \Delta GHI é escaleno.
\overline{GH} \neq \overline{HI} \neq \overline{IG}
Classificação de triângulos de acordo com seus ângulos
Triângulo retângulo
Os triângulos retângulos são aqueles que têm um ângulo reto. A hipotenusa é o lado oposto ao ângulo reto e os lados que formam o ângulo reto são chamados de pernas.
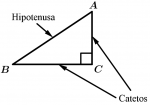
O \Delta ABC é retângulo.
\measuredangle C = 90^{\text{o}}
Triângulo agudo
Triângulos agudos são aqueles que têm seus três ângulos agudos.
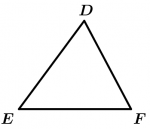
O \Delta DEF é agudo.
O \measuredangle D, o \measuredangle E e o \measuredangle F são agudos.
Triângulo equiangular
Triângulo equiangular é chamado para aqueles que têm ângulos iguais, e sim, eles são triângulos equiláteros.
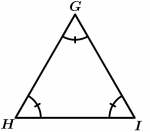
O \Delta GHI é equiangular.
\measuredangle G = \measuredangle H = \measuredangle I
Triângulo obtuso
Os triângulos obtusos são aqueles que apresentam um ângulo obtuso. O ângulo obtuso é aquele ângulo que mede mais de 90 ° e menos de 180 °.
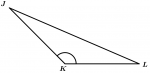
O \Delta JKL é obtuso.
90^{\text{o}} < \measuredangle K < 180^{\text{o}}
Triângulo oblíquo
É todo esse triângulo que não é retángulo. Ângulo oblíquo significa qualquer ângulo que não é reto.
Obrigado por estar conosco neste momento :)
