Classificação de polígonos

Os polígonos são classificados de acordo com seu número de lados, de acordo com seus ângulos e também são classificados de acordo com a igualdade ou desigualdade de seus ângulos e lados, ou seja, se são regulares ou irregulares.

Classificação de acordo com o número de lados

\begin{array}{| c | c |} \hline \text{Polígonos} & \text{Número de lados} \\ \hline \hline \text{Triângulo} & 3 \\ \hline \text{Quadrilátero} & 4 \\ \hline \text{Pentágono} & 5 \\ \hline \text{Hexágono} & 6 \\ \hline \text{Heptágono} & 7 \\ \hline \text{Octógono} & 8 \\ \hline \text{Nonagon ou eneagon} & 9 \\ \hline \text{Decágono} & 10 \\ \hline \text{Hendecágono ou undecágono} & 11 \\ \hline \text{Dodecágono} & 12 \\ \hline \text{Tridecágono} & 13 \\ \hline \text{Tetradecágono} & 14 \\ \hline \text{Pentadecágono} & 15 \\ \hline \text{Hexadecágono} & 16 \\ \hline \text{Heptadecágono} & 17 \\ \hline \text{Octadecágono} & 18 \\ \hline \text{Nonadecágono} & 19 \\ \hline \text{Icoságono} & 20 \\ \hline \end{array}

Os polígonos que têm mais de 20 lados são conhecidos como os n-agons, isso é feito para uma melhor facilidade de compreensão, já que os polígonos de mais de 20 lados têm nomes não muito comuns que certamente não muitos ouviram, de qualquer maneira, vou citar alguns desses polígonos abaixo para que você possa ver o nome que foi atribuído a eles:

\begin{array}{| c | c |} \hline \text{Polígonos} & \text{Número de lados} \\ \hline \hline \text{Icosakaihegon} & 21 \\ \hline \text{Icosakaidígono} & 22 \\ \hline \text{Icosakaitrígono} & 23 \\
\hline \text{Icosakaitetragon} & 24 \\ \hline \text{Icosakaipentagon} & 25 \\ \hline \text{Icosakaihexagon} & 26 \\ \hline \text{Icosakaiheptágono} & 27 \\ \hline \text{Icosakaioctagon} & 28 \\ \hline \text{Icosakaieneagon} & 29 \\ \hline \end{array}

Sim, entendo, é melhor dizer: “polígono de n lados” quando o polígono tem mais de 20 lados.

Classificação de acordo com seus ângulos

Dependendo do ângulo formado pelos pares de lados consecutivos do polígono, são classificados como côncavos ou convexos.

Polígonos côncavos

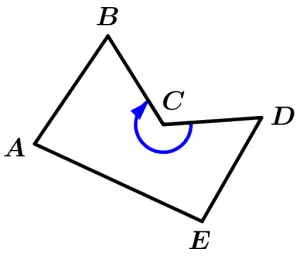
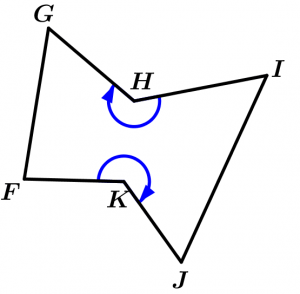
Quando contêm um ou mais ângulos internos com medidas maiores que 180 ° são chamados côncavos, significa que a concavidade é observada de fora do polígono.

Polígonos convexos

Eles são convexos quando a medida de todos os ângulos internos são menores que 180 °, o que implica que a convexidade é observada do lado de fora do polígono.

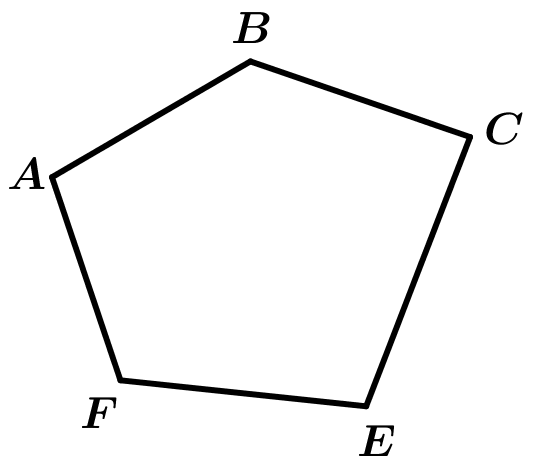
Como você deve ter notado, a concavidade e a convexidade são observadas do lado de fora do polígono, então simplesmente podemos saber se um polígono é classificado como côncavo ou convexo.

Classificação de acordo com a igualdade ou desigualdade de ângulos e lados

O título se refere se temos um polígono regular ou se temos um polígono irregular.

Polígonos regulares

Polígonos regulares são aqueles que possuem lados e ângulos iguais, ou seja, são equiláteros e equiangulares. Há momentos em que dizemos que um polígono é equilátero ele já é regular, mas atenção, como mencionamos: nem todos os polígonos equiláteros são regulares, mas todos os polígonos regulares são equiláteros. O mesmo é verdade quando mencionamos polígonos equiangulares: nem todos os polígonos equiangulares são regulares, mas todos os polígonos regulares são equiangulares. Vejamos alguns exemplos de polígonos regulares:

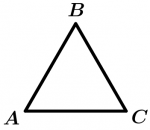
\text{Triângulo } ABC \text{ é regular}

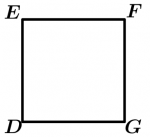
\text{Quadrilátero } DEFG \text{ é regular}

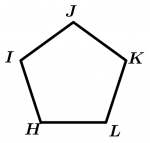
\text{Pentágono } HIJKL \text{ é regular}

Polígonos irregulares

Polígonos irregulares são aqueles que têm lados desiguais, ângulos desiguais ou ambos.

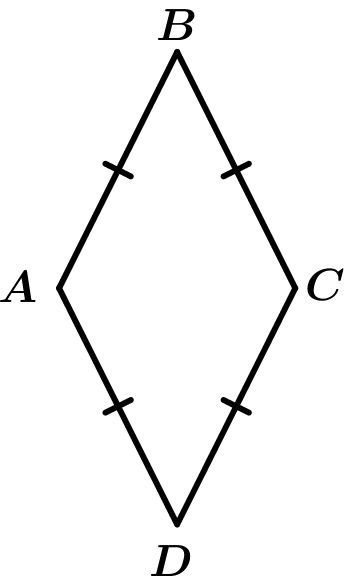
Vamos com um exemplo de rombo, este é um polígono equilátero porque tem lados iguais, mas tem ângulos desiguais, portanto é um polígono irregular:

O exemplo a seguir mostra um quadrilátero que é equiangular, mas é irregular, vejamos o retângulo:

Agora vamos ver mais um exemplo, um polígono que não é equiangular nem equilátero, um simples quadrilátero:

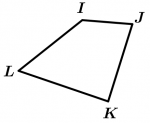
As três figuras acima mencionadas são irregulares, só queria enfatizar que não por serem equiláteros ou equiangulares, já são consideradas regulares. A única figura que pela força é equilátero, é equiangular e vice-versa … essa figura é o triângulo equilátero.

Obrigado por estar conosco neste momento : )