En el concepto de hipérbola, A y A' siempre se utilizarán para representar los vértices, y B y B' se utilizan para representar los extremos del segmento perpendicular al segmento \overline{AA'}. Primero que nada, quiero aclarar que con un poco de práctica ya se podrá discernir cuando a es menor o mayor que b y saber si la hipérbola abre hacia arriba y abajo o hacia la derecha e izquierda.
Partes de la hipérbola con centro en C(x_{0},y_{0}) y segmento \overline{AA'} paralelo al eje x
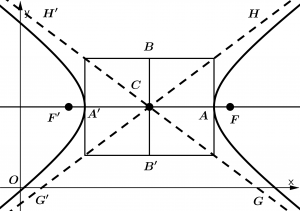
Veamos nuestra figura base de la hipérbola gráfica con la que definiremos las fórmulas y los elementos de la hipérbola:
Ecuaciones de la hipérbola en coordenadas rectangulares:
La ecuación de la hipérbola que abre hacia la derecha e izquierda tiene la peculiaridad de que el signo de la fracción que contiene a las y‘s va a ser negativo:
\cfrac{(x - x_{0})^{2}}{a^{2}} - \cfrac{(y - y_{0})^{2}}{b^{2}} = 1
Las coordenadas x_{0} y y_{0} siempre representan el centro C para cualquier hipérbola, no importa si es una hipérbola que abre hacia la derecha e izquierda o una hipérbola que abre hacia arriba y abajo.
- c representa la longitud del segmento \overline{CF} donde \overline{CF} =\overline{CF'}.
- a representa la longitud del segmento \overline{CA} donde \overline{CA}=\overline{CA'}.
- b representa la longitud del segmento \overline{CB} donde \overline{CB}=\overline{CB'}.
Longitud del segmento \overline{AA'}
La longitud del segmento \overline{AA'} es 2a.
Longitud del segmento \overline{BB'}
La longitud del segmento \overline{BB'} es 2b.
Longitud del centro a los focos (c)
La distancia que hay del centro C a los focos F o a F' es:
c = \sqrt{a^{2} \ + b^{2}}
Excentricidad de la hipérbola
La fórmula para calcular la excentricidad de la hipérbola es la siguiente:
\epsilon = \cfrac{c}{a}
La excentricidad sólo puede tomar valores mayores que 1: \epsilon > 1, pero ahora:
¿Qué significa la excentricidad en la hipérbola o qué representa?
Significa que si el valor de la excentricidad es más cercana a 1, la hipérbola tiende a ser una recta que se le quitó un segmento (esto ocurre porque la hipérbola se ve tan cerrada que parece una recta), y mientras más grande sea el valor de la excentricidad, la hipérbola tiende a parecerse a un par de rectas paralelas.
Pendientes de las asíntotas de la hipérbola
Las pendientes de las asíntotas de la hipérbola \overline{G'H} y \overline{GH'} se calculan dividiendo el valor del segmento vertical entre el segmento horizontal:
= \pm \cfrac{\text{segmento vertical}}{\text{segmento horizontal}}
El símbolo \pm significa que se van a utilizar los dos signos ya que la hipérbola tiene dos asíntotas, lo que quiere decir es que la pendiente que obtengamos va a ser positiva y negativa por sus dos asíntotas, en un momento lo veremos con un ejemplo.
Punto de la hipérbola hacia los dos focos
Si P es un punto cualquiera de la hipérbola, PF \ - PF' = \pm 2a. El símbolo \pm depende de la rama.
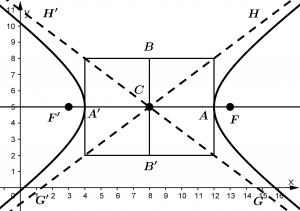
Ejemplo de hipérbola con centro en el origen C(x_{0},y_{0}) y con segmento \overline{AA'} paralelo al eje x
La ecuación de la hipérbola es:
\cfrac{(x - 8)^{2}}{4^{2}} - \cfrac{(y - 5)^{2}}{3^{3}} = 1
El centro de la hipérbola
Como se puede observar, el centro C de la hipérbola se encuentra en:
C(8,5)
Eso quiere decir que el centro de nuestra hipérbola se encontrará en los valores que tenga x_{0} y y_{0} sólo que colocaremos el signos contrario en nuestra coordenada, eso quiere decir que como nuestro valor de x_{0} es -8 y nuestro valor de y_{0} es -5, entonces nuestra coordenada del centro de la hipérbola será C(8,5).
Longitud del segmento \overline{AA'}
La longitud del segmento \overline{AA'} es igual a 8, lo que quiere decir que la longitud de a es igual a 4.
Longitud del segmento \overline{BB'}
La longitud del segmento \overline{BB'} es igual a 6, lo que quiere decir que la longitud de b es igual a 3.
Distancia del centro a los focos
La distancia del centro C a cualquiera de los dos focos, ya sea F o F' es:
c = \sqrt{4^{2} + 3^{2}} = \sqrt{16 + 9} = \sqrt{25} = 5
Entonces el foco F está en el punto F(13,5) y el foco F' está en el punto F'(3,5).
Excentricidad de la hipérbola
\epsilon = \cfrac{c}{a} = \cfrac{5}{4}=1.25
Pendientes de las asíntotas de la hipérbola
El cálculo de las pendientes de las asíntotas es muy sencillo, dividiremos la longitud del segmento vertical entre la longitud del segmento horizontal:
\pm \cfrac{\text{segmento vertical}}{\text{segmento horizontal}} = \pm \cfrac{3}{4} = \pm 0.75
Entonces la pendiente de una asíntota es 0\text{.}75 y la pendiente de la otra asíntota es -0\text{.}75.
Punto de la hipérbola hacia los dos focos
Puedes hacer rápido esta demostración agarrando como P cualquier vértice de la hipérbola y verás fácilmente que se demuestra la fórmula PF \ - PF' = \pm 2a. Intenta tomando el vértice (4,5).
¿Por qué no es práctico llamar “eje mayor” y “eje menor” a los ejes de la hipérbola?
Simple y sencillamente porque habría confusión a la hora de utilizar las fórmulas, observa las siguientes gráficas
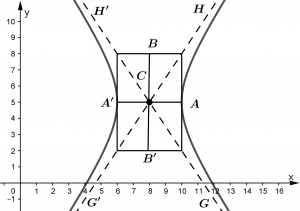
Gráfica de la hipérbola 1
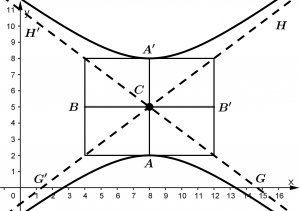
Gráfica de la hipérbola 2
En la Gráfica de la hipérbola 1 (que es la de nuestro ejemplo) si mencionamos al eje mayor tomaremos al segmento \overline{A'A}, y si mencionamos al eje menor tomaremos al segmento \overline{B'B}, hasta ahorita vamos bien. ¿Pero que pasaría si te digo que tomes el eje mayor de la Gráfica de la hipérbola 2? El eje mayor ahora ya no es \overline{A'A}, ¿verdad?
Si estudiando las fórmulas quieres determinar las pendientes de las rectas asíntotas de la Gráfica de la hipérbola 2 y te aprendiste la fórmula de la siguiente manera:
\pm \cfrac{\text{eje menor}}{\text{eje mayor}}
Te darás cuenta que ahora el eje menor es horizontal y el eje mayor es vertical, lo que significa que la pendiente que obtengas no dará como resultado la pendiente de tus asíntotas de tu Gráfica de la hipérbola 2. Así que para hallar la pendiente de las asíntotas de la hipérbola acostumbrémonos a llamar a los ejes como “segmento vertical” y “segmento horizontal”.
\pm \cfrac{\text{segmento vertical } }{\text{segmento horizontal}}
Hipérbola con centro en C(x_{0},y_{0}) y segmento \overline{AA'} paralelo al eje y
Observa el siguiente ejemplo:
La cual su ecuación es:
\cfrac{(y - 5)^{2}}{3^{2}} - \cfrac{(x - 8)^{2}}{4^{2}} = 1
Cuando la hipérbola abre hacia arriba y hacia abajo, el denominador de la fracción que tiene las y‘s ahora será a y el denominador de la fracción que tiene las x‘s ahora será b. Lo que quiere decir que la ecuación para las hipérbolas que abren hacia arriba y hacia abajo es:
\cfrac{(y - y_{0})^{2}}{a^{2}} - \cfrac{(x - x_{0})^{2}}{b^{2}} = 1
Se dice que la a sigue al signo positivo y la b sigue al signo negativo, pero todas las fórmulas mencionadas se usan exactamente igual.
Gracias por estar en este artículo con nosotros : )